Two-way string-matching algorithm
|
Read other articles:

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.Este aviso fue puesto el 26 de enero de 2021. Prunus sp. en el parque Takaoka Kojo. Flor de cerezo o Sakura La sakura (桜 o さくら, '?), la flor de cerezo o el cerezo japonés es uno de los símbolos más conocidos de la cultura japonesa. También se nombra sakura a tres especies de plantas del género Prunus. Florecimiento Vista de varias flores de un árbol de cerezo en Fukushima, Japón. El cere...

Selección de fútbol sub-17 de España Datos generalesPaís EspañaCódigo FIFA ESPFederación Real Federación Española de FútbolConfederación UEFASeudónimo(s) La RojitaSeleccionador José LanaMás goles Diego MonrealAbel Ruiz (27)Más partidos Abel Ruiz (37)Equipaciones Primera Segunda Mejor(es) resultado(s) España 13 - 0 Nueva Zelanda Ismailía, Egipto — 11 de septiembre de 1997Copa Mundial de Fútbol Sub-17Peor(es) resultado(s) Sin datosCopa MundialParticipaciones 11 (primer...

此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2017年2月4日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目體裁可能更适合散文而非列表。 (2017年2月4日)如果合适请协助将此条目改写为散文。查看编辑帮助。 香港粵語配音員的職責是以粵語為電視劇、電影、動畫以及電視廣告配音,一般以工作量或合約制獲取报酬。粵語配音员分兩派,...

山口 俊 読売ジャイアンツ時代(2019年10月9日 東京ドーム)基本情報国籍 日本出身地 大分県中津市生年月日 (1987-07-11) 1987年7月11日(36歳)身長体重 187 cm98 kg選手情報投球・打席 右投右打ポジション 投手プロ入り 2005年 高校生ドラフト1巡目初出場 NPB / 2006年6月29日MLB / 2020年7月26日最終出場 MLB / 2020年9月28日NPB / 2022年4月8日経歴(括弧内はプロチーム在籍年度) 柳ヶ浦高等...

Protein-coding gene in the species Homo sapiens YWHAZAvailable structuresPDBOrtholog search: PDBe RCSB List of PDB id codes1IB1, 1QJA, 1QJB, 2C1J, 2C1N, 2O02, 2WH0, 3CU8, 3NKX, 3RDH, 4BG6, 4FJ3, 4HKC, 4IHL, 4N7G, 4N7Y, 4N84, 4WRQ, 4ZDR, 1A38, 1A4O, 1A37, 5D2D, 5D3F, 5EXA, 5EWZIdentifiersAliasesYWHAZ, 14-3-3-zeta, HEL-S-3, HEL4, KCIP-1, YWHAD, HEL-S-93, tyrosine 3-monooxygenase/tryptophan 5-monooxygenase activation protein zeta, POPCHASExternal IDsOMIM: 601288 MGI: 109484 HomoloGene: 56528 Gen...

Australian news website The topic of this article may not meet Wikipedia's notability guideline for web content. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: News.com.au – news · newspapers · books · scholar...

KingsmeadowNama lengkapKingsmeadowLokasiJack Goodchild Way, Kingston upon Thames, London, InggrisOperatorChelseaKapasitas4.850 (2.265 kursi)Ukuran lapangan110 x 75 kakiPermukaanRumputKonstruksiDidirikan1989Dibuka1989PemakaiKingstonian F.C. (1989–2017)AFC Wimbledon (2002–2020) Chelsea Wanita (2017–) Akademi Chelsea (2020–) Kingsmeadow adalah stadion sepak bola di Norbiton, Kingston upon Thames, London, yang merupakan kandang dari Chelsea Wanita dan Chelsea U-23. Sebelumnya digunakan Ki...
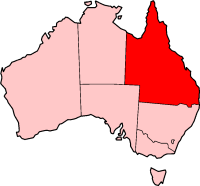
Queensland, Australia Queensland is the second-largest state in Australia but has the greatest biodiversity, with 684 species of bird recorded (more than closest-rivals New South Wales or West Australia with both around 550). The high avian biodiversity is probably a reflection of the wide variety of habitats, from desert to rainforest and mangrove forest to mulga, which make Queensland a birders paradise. This list is based on the 1996 classification by Sibley and Monroe (though there has be...

野村周平男演员原文名野村 周平罗马拼音Nomura Shuhei国籍 日本民族中日混血兒 (漢族, 大和族)籍贯兵庫縣出生 (1993-11-14) 1993年11月14日(30歲) 日本兵庫縣职业演員语言日語、漢語、英語教育程度堀越高等學校出道地点 日本活跃年代2009年至今经纪公司Amuse网站Amuse官方網站互联网电影数据库(IMDb)信息 日語寫法日語原文野村 周平假名のむら しゅうへい平文式罗马�...

Pretender to the French throne Jean d'OrléansCount of ParisOrléanist pretender to the French throneas Jean IVTenure21 January 2019 – presentPredecessorHenri VIIHeir apparentGaston, Dauphin of FranceBorn (1965-05-19) 19 May 1965 (age 58)Boulogne-Billancourt, FranceSpouse Philomena de Tornos Steinhart (m. 2009)Issue Prince Gaston, Count of Clermont Princess Antoinette Princess Louise-Marguerite Prince Joseph Princess Jacinthe NamesJean Carl Pierre...

Jim LeRoy in Bulldog Jim LeRoy (5 de abril de 1961 – 28 de julio de 2007) fue un piloto de acrobacias estadounidense. Perteneció al Cuerpo de Marines de los Estados Unidos, como Scout (reconocimiento aéreo)/Francotirador, tuvo un grado B.S. en Ingeniería Aeronáutica/Aeroespacial, así como la Licencia de Mantenimiento de Aeronaves. Experiencia profesional Empezando con actuaciones en solitario, se ganó una reputación con sus exhibiciones acrobáticas de gran energía. En el año 2003,...

City in Iowa, United StatesStrawberry Point, IowaCityLocation of Strawberry Point, IowaCoordinates: 42°40′45″N 91°32′13″W / 42.67917°N 91.53694°W / 42.67917; -91.53694Country United StatesState IowaCountyClaytonArea[1] • Total2.09 sq mi (5.41 km2) • Land2.09 sq mi (5.41 km2) • Water0.00 sq mi (0.00 km2)Elevation1,220 ft (372 m)Population (2020)&...

° Leestekens aanhalingstekens („ ”, “ ”, , ‘ ’, ' ' ) accolade ( { } ) afbreekteken ( - ) apostrof ( ’ ) beletselteken ( … ) dubbelepunt ( : ) gedachtestreepje ofkastlijntje ( –, — ) guillemets ( « » ) haakjes ( ( ), [ ], ⟨ ⟩ ) komma ( , ) koppelteken ( - ) liggend streepje ( -, –, —, _ ) omgekeerd uitroepteken ( ¡ ) omgekeerd vraagteken ( ¿ ) punt ( . ) puntkomma ( ; ) schuine streep ( / ) uitroepteken ( ! ) vraagteken...

Down Under Men at Work Veröffentlichung Oktober 1981 (Album) November 1981 (Single)[1] Länge 3:42 Genre(s) Pop-Rock. Reggae Autor(en) Colin Hay, Ron Strykert Produzent(en) Peter McIan Album Business as Usual Down Under ist ein Song der australischen Band Men at Work. Das Stück ist im Reggae-Rhythmus gehalten, und der Text befasst sich mit australischen Eigenheiten. Das Lied ist auf dem im Oktober 1981 veröffentlichten Debütalbum der Band, Business as Usual, enthalten und wurde im...

Festival in India This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (January 2017) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material ...

250 kW steam turbine generator set (1910) 500 MW Siemens multi stage steam turbine with generator set (rear, red) Parsons first 1 MW steam turbine driven Turbogenerator (made 1900 for a plant in Elberfeld, Germany) Ottó Bláthy in the armature of a Ganz turbo generator (1904) Small RP4 steam turbo generator set 500W/24V for a steam locomotive: alternator (left) + turbine (right) A turbo generator is an electric generator connected to the shaft of a steam turbine or gas turbine...

2018 mobile game This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may require copy editing for grammar, style, cohesion, tone, or spelling. You can assist by editing it. (October 2023) (Learn how and when to remove this template message) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced...

Palatial compound in Addis Ababa, Ethiopia; residence of Prime Minister of Ethiopia Menelik II Palaceየምኒልክ ግቢThe Imperial Palace around 1934Former namesMenelik II PalaceAlternative namesImperial Palace or Great GhebbiGeneral informationLocationAddis Ababa, EthiopiaCoordinates9°01′29″N 38°45′48″E / 9.0248°N 38.7633°E / 9.0248; 38.7633Construction started1890Technical detailsSize36 hectaresWebsitewww.unitypark.et The Menelik Palace, also known a...

Building in Old City , AzerbaijanBaku Khans' PalaceBakı xanları sarayıOne of the buildings, Boyuk Gala Street, 46.General informationArchitectural styleTypical Absheron houseLocationOld City (Baku)CountryAzerbaijanCoordinates40°22′05″N 49°50′12″E / 40.3681°N 49.8367°E / 40.3681; 49.8367Construction started17th or 18th century Baku Khans' Palace (Azerbaijani: Bakı xanları sarayı) is a complex of several houses that belonged to the members of the ruling...

北門神社北門神社/ほくもんじんじゃ Hokumon jinjya北門神社第一鳥居、石燈籠、第二鳥居、拜殿基本信息位置 日治臺灣臺南州北門郡佳里街佳里宗教神道主祭神天照大神、大國魂命、大己貴命、少彥名命、北白川宮能久親王例祭10月28日社格鄉社建筑详情建立昭和六年(1936年)拆毁时间不明 北門神社是台灣日治時期位於北門郡佳里街的神社,1936年鎮座,1944年升格為鄉社...

