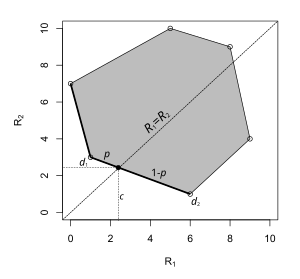
Minimax estimator
|
Read other articles:
Den här artikeln har skapats av Lsjbot, ett program (en robot) för automatisk redigering. (2014-07)Artikeln kan innehålla fakta- eller språkfel, eller ett märkligt urval av fakta, källor eller bilder. Mallen kan avlägsnas efter en kontroll av innehållet (vidare information) Rhododendron brevipetiolatumSystematikDomänEukaryoterEukaryotaRikeVäxterPlantaeDivisionKärlväxterTracheophytaKlassTvåhjärtbladiga blomväxterMagnoliopsidaOrdningLjungordningenEricalesFamiljLjungväxterEricace...

Game Boy Color (GBC) Разработчик Nintendo Research & Engineering Department[d] Производитель Nintendo Тип Портативная игровая система Поколение Пятое поколение Дата выхода 21 октября 1998 года 18 ноября 1998 года 23 ноября 1998 года 27 ноября 1998 года сентябрь 2000 года 2001 год Поддержка прекращена 23 марта 2003 года П�...

Wappen Deutschlandkarte 50.50916666666711.138333333333830Koordinaten: 50° 31′ N, 11° 8′ O Basisdaten Bundesland: Thüringen Landkreis: Sonneberg Erfüllende Gemeinde: für Goldisthal Höhe: 830 m ü. NHN Fläche: 108,22 km2 Einwohner: 8927 (31. Dez. 2022)[1] Bevölkerungsdichte: 82 Einwohner je km2 Postleitzahl: 98724 Vorwahlen: 03679, 036701 Kfz-Kennzeichen: SON, NH Gemeindeschlüssel: 16 0 72 013 LOCODE: DE N...

Voor het Belgische marionettentheater, zie Koninklijk Poppentheater Toone. Toone Plaats in de Verenigde Staten Vlag van Verenigde Staten Locatie van Toone in Tennessee Locatie van Tennessee in de VS Situering County Hardeman County Type plaats Town Staat Tennessee Coördinaten 35° 21′ NB, 88° 57′ WL Algemeen Oppervlakte 2,1 km² - land 2,1 km² - water 0,0 km² Inwoners (2006) 357 Hoogte 125 m Overig ZIP-code(s) 38381 FIPS-code 74640 Portaal Verenigde Staten Toone i...

Text placed alongside its translation or translations Not to be confused with Parallel novel. The Rosetta Stone, a stele engraved with the same decree in both of the Ancient Egyptian scripts as well as Ancient Greek. Its discovery was key to deciphering the Ancient Egyptian language. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Parallel tex...

University in Can Tho, Vietnam This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Can Tho University – news · newspapers · books · scholar · JSTOR (April 2020) (Learn how and when to remove this template message) Can Tho UniversityTrường Đại học Cần ThơEstablished1966PresidentHà Thanh ToànVice-pres...

Ukrainian far-right politician and military commander In this name that follows Eastern Slavic naming conventions, the patronymic is Yevheniyovych and the family name is Biletsky. Andriy BiletskyАндрій БілецькийBiletsky in 2017Leader of National CorpsIncumbentAssumed office 14 October 2016People's Deputy of UkraineIn office27 November 2014 – 24 July 2019Preceded byOleksandr Bryhynets [uk]Succeeded byMaryana BezuhlaConstituencyKyiv, No. 217Command...

French nationalist movement L'Œuvre Française PrésideurPierre Sidos (1968–2012)Yvan Benedetti (2012–2013)Founded1968; 55 years ago (1968)DissolvedJuly 23, 2013 (2013-07-23)NewspaperLe Soleil (1968–1993)Jeune Nation (1994–2013)Youth wingJeunesses NationalistesMembership (2013)400IdeologyFrench nationalismNeo-PétainismAntisemitismPolitical positionFar-rightReligionCatholic ChurchColoursBlue, White, RedPolitics of FrancePolitical partiesElections...

Arnaques, Crimes et Botanique Données clés Titre québécois Arnaques, Combines et Botanique Titre original Lock, Stock and Two Smoking Barrels Réalisation Guy Ritchie Scénario Guy Ritchie Musique David A. HughesJohn Murphy Acteurs principaux Nick MoranJason StathamJason FlemyngDexter Fletcher Sociétés de production Summit EntertainmentSteve Tisch CompanySKA FilmsHandMade FilmsPolygram Filmed Entertainment Pays de production Royaume-Uni Genre Comédie noire, film de gangsters Durée 107...

Australian soccer player Katarina Jukic Jukic playing for East Fremantle in 2010Personal informationDate of birth (1989-11-23) 23 November 1989 (age 34)Place of birth Perth, Western Australia, AustraliaHeight 1.63 m (5 ft 4 in)Position(s) Midfielder / StrikerYouth career FW NTCSenior career*Years Team Apps (Gls)2008–2010 Perth Glory 9 (0)2011–2012 Perth Glory 10 (2)2013–2015 Perth Glory 0 (0)2018 Queen's Park FC 2019–2021 Perth Glory 19 (1) *Club domestic league ap...

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (beispielsweise Einzelnachweisen) ausgestattet. Angaben ohne ausreichenden Beleg könnten demnächst entfernt werden. Bitte hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Siehe Diskussionsseite. Die Korpuslinguistik ist ein Bereich der Sprachwissenschaft. Darin werden neue Erkenntnisse über Sprache generell oder über bestimmte einzelne Sprachen erlangt oder bestehende Hypothesen über...

2011 novel by Julie Otsuka The Buddha in the Attic First editionAuthorJulie OtsukaCountryUnited StatesLanguageEnglishPublishedAlfred A. KnopfAwardsPEN/Faulkner Award for FictionPreceded byWhen the Emperor was Divine The Buddha in the Attic is a 2011 novel written by American author Julie Otsuka about Japanese picture brides immigrating to America in the early 1900s.[1] It is Otsuka's second novel. The novel was published in the United States in August 2011 by the publishing...

H.Dani AnwarWakil Ketua Dewan Perwakilan Rakyat Daerah Provinsi DKI JakartaMasa jabatan19 Juni 2008 – 25 Agustus 2009Menjabat bersama Ilal Ferhard dan Maringan PangaribuanPresidenSusilo Bambang YudhoyonoGubernurFauzi BowoKetuaAdi SurapriatnaPendahuluAhmad HeryawanPengganti Periode 2009–14 Triwisaksana Sayogo Hendrosubroto Inggard Joshua Abraham Lunggana Anggota Dewan Perwakilan Rakyat Daerah Provinsi DKI JakartaMasa jabatan26 Agustus 2019 – 3 Agustus 2020Pengga...

العلاقات الإستونية الليبيرية إستونيا ليبيريا إستونيا ليبيريا تعديل مصدري - تعديل العلاقات الإستونية الليبيرية هي العلاقات الثنائية التي تجمع بين إستونيا وليبيريا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ال�...

American actor This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Eric Christian Olsen – news · newspapers · books · scholar · JSTOR (November 2015) (Learn how and when to remove this template mess...

High school in Monmouth County, New Jersey, United States For the school in Allentown, Pennsylvania known as Allentown High School 1858–1960, see William Allen High School. Allentown High SchoolAddress27 High StreetAllentown, Monmouth County, New Jersey 08501United StatesCoordinates40°10′28″N 74°35′16″W / 40.174416°N 74.587791°W / 40.174416; -74.587791InformationTypePublic high schoolEstablished1924School districtUpper Freehold Regional School DistrictNCE...

خدمة المارشالات الأمريكية خدمة المارشالات الأمريكية خدمة المارشالات الأمريكية الاختصار (بالإنجليزية: USMS) البلد الولايات المتحدة المقر الرئيسي مقاطعة أرلنغتون، فيرجينيا تاريخ التأسيس 1789 المنظمة الأم وزارة العدل الأمريكية عدد الموظفين 5116 الم...

Treaty of Bangkok redirects here. For other uses, see Treaty of Bangkok (disambiguation). Treaty of Southeast Asia Nuclear Weapon-Free ZoneParticipation in the Southeast Asian Nuclear-Weapon-Free Zone Treaty includes all of ASEANTypenuclear disarmamentSigned15 December 1995LocationBangkokEffectiveMarch 28, 1997Parties10 The Southeast Asian Nuclear-Weapon-Free Zone Treaty (SEANWFZ), or the Bangkok Treaty of 1995, is a nuclear weapons moratorium treaty between 10 Southeast Asian member-states u...

Anti Gas SkinSutradara Kim Gok and Kim Seon Produser Choi Doo-young Ditulis olehKim Seon[1]SkenarioKim Seon[1]PemeranPark Ji-hwan, Jang Liu, Cho Young-jin, Patrick SmithTanggal rilis 22 Agustus 2013 (2013-08-22) Durasi123 menitNegara Korea Selatan Bahasa Korea Anti Gas Skin (bahasa Korea: 방독피 RR: Bang Dok Pi) adalah film Korea Selatan tahun yang disutradara oleh saudara kembar Kim Gok and Kim Seon. Para sutradara menggambarkan Anti Gas Skin sebagai sindiran poli...

Plateau de Beille Top 2001 m Coördinaten 42° 44′ NB, 1° 41′ OL Locatie Pyreneeën, Frankrijk Startplaats Les Cabannes Hoogteverschil 1255 m Lengte 15.900 m Stijgings-% 7,9% Steilste km 10,8% Portaal Wielersport Plateau de Beille is een wintersportoord in de Franse Pyreneeën. De plaats ligt in de regio Occitanie in het departement Ariège. Het wintersportstation ligt op een hoogte van 1780 meter. Ronde van Frankrijk Beklimming in 2007 Plateau de Beille is zes maal...



























![{\displaystyle \pi _{n}\sim U[-n,n]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29793e7c3001cca259454e530c2b23a626264fcc)