Jet (particle physics)
|
Read other articles:

Chinese sovereign wealth fund China Investment CorporationHeadquarters at New Beijing Poly PlazaTypeSovereign wealth fundIndustryInvestment serviceFounded2007HeadquartersBeijing, ChinaKey peoplePeng Chun (Chairman and CEO) Ju Weimin (Vice Chairman, President and CIO)Operating income US$ 118.012 billion (2019)[1]Net income US$ 110.313 billion (2019)[1]AUM CNY5.58 trillion (2021) US$0.87 trillion[2]Total assets US$ 1,350 billon (2023)Total equity US$ 94...

Eduardo Oscar Camaño Eduardo CamañoEduardo Oscar Camaño Presidente da Argentina (interino) Período 30 de dezembro de 2001a 1 de janeiro de 2002 Vice-presidente Nenhum Antecessor(a) Adolfo Rodríguez Saá Sucessor(a) Eduardo Alberto Duhalde Dados pessoais Nascimento 17 de junho de 1946 (77 anos) Buenos Aires, Argentina Nacionalidade argentino Partido Partido Justicialista Profissão advogado Eduardo Oscar Camaño (Buenos Aires, 17 de junho de 1946) é um político argentino do Pa...

Ця стаття про книгу. Про екранізацію див. Сало, або 120 днів Содому. 120 днів Содому, або Школа розпустифр. Les 120 Journées de Sodome ou l'école du libertinage Титульна сторінка першого видання 1904 рокуЖанр еротика, порнографія, романФорма романТема садомазохізмАвтор Маркіз де СадМова французькаНа

En mathématiques, le plan complexe (aussi appelé plan d'Argand, plan d'Argand-Cauchy ou plan d'Argand-Gauss[1]) désigne un plan, muni d'un repère orthonormé, dont chaque point est la représentation graphique d'un nombre complexe unique. Le nombre complexe associé à un point est appelé l'affixe de ce point. Une affixe est constituée d'une partie réelle et d'une partie imaginaire correspondant respectivement à l'abscisse et l'ordonnée du point. Définition Représentation graphique...

Handley Page Type G Vista trasera del Type G. Tipo Biplano biplazaFabricante Handley Page Aircraft CompanyDiseñado por Frederick Handley PagePrimer vuelo 6 de noviembre de 1913[1]Retirado 1915N.º construidos 1[editar datos en Wikidata] El Handley Page Type G fue un biplano biplaza británico, diseñado por Handley Page, que voló por primera vez en 1913. Sólo se construyó un ejemplar. Diseño y desarrollo Vista lateral del Type G. El Type G fue el primer biplano diseñado...

Jepang Artikel ini adalah bagian dari seri Politik dan KetatanegaraanJepang Konstitusi Konstitusi Jepang Sejarah Hukum Monarki Kaisar (daftar) Akihito Putra Mahkota Naruhito Istana Kaisar Badan Rumah Tangga Kekaisaran Badan legislatif Parlemen Jepang Dewan Perwakilan Rakyat Ketua Tadamori Ōshima Wakil Ketua Hirotaka Akamatsu Majelis Tinggi Presiden Chuichi Date Wakil Presiden Akira Gunji Pemimpin Oposisi Yukio Edano Eksekutif Perdana Menteri (daftar) Shinzō Abe Wakil Perdana Menteri Tarō A...

Salah satu motif Batik Pringgondani Batik Pringgondani (aksara Jawa: ꦥꦿꦶꦁꦒꦺꦴꦤ꧀ꦢꦤꦶ) adalah salah satu motif batik Jawa, Indonesia. Pringgondani atau pringgodani adalah nama sasana kesatriyan tempat tinggal Gatotkaca putra Werkudara. Corak ini umumnya dirancang dalam warna-warna gelap seperti biru nila dan soga-coklat. Ragam hias yang ditampilkan adalah tatanan rumit penuh sulur-suluran kecil yang diselingi dengan naga.[1] Asal kata Pringgondani dalam bahasa Jawa...

Joshua A. Lomberger Josh Mathews 2010 Personalia Geburtstag 25. November 1980 Geburtsort Sea Isle City, New Jersey Karriereinformationen Ringname(n) Josh Mathews Körpergröße 175 Kampfgewicht 65 Angekündigt aus Sea Isle City, New Jersey Promotion WWE Tough Enough Staffel 1World Wrestling Entertainment (2002–2015)Global Force Wrestling (seit 2015) Trainiert von Al SnowJacqueline MooreTazzTori Debüt 2001 (als Wrestler) Josh Mathews (* 25. November 1980 in Sea Isle City, New Jersey als Jos...

Live at the MarqueeAlbum live karya Dream TheaterDirilis3 September 1993DirekamThe Marquee Club di London, 23 April 1993GenreProgressive metal, progressive rockDurasi51:33LabelAtco RecordsKronologi Dream Theater Images and Words(1992)Images and Words1992 Live at the Marquee (1993) Awake(1994)Awake1994 Penilaian profesional Skor ulasan Sumber Nilai Allmusic [1] Live at Marquee adalah album live yang direkam di London Marquee Club oleh band progressive metal / rock Dream Theater. Da...

Quantified characteristic in role-playing games Part of a series onRole-playing games Types Tabletop Live action Video game Forum Topics Campaign setting Character creation History System Theory GNS theory Threefold model Terminology Terms Actual play Adventure Gamemaster Player character Non-player character Statistic Lists Campaign settings LARP groups Production Artists Designers Publishers Games Tabletop WikiProjectvte This article needs additional citations for verification. Please help ...

Stephen Payn was Dean of Exeter between 1415 and 1419.[1] He was preceded by Ralph Tregrision and followed by John Cobethorn. Notes ^ Ursula Radford (1955). An Introduction to the Deans of Exeter. Report & Transactions of the Devonshire Association 87: 1–24. Catholic Church titles Preceded byRalph Tregrision Dean of Exeter 1415–1419 Succeeded byJohn Cobethorn vteDeans of ExeterHigh Medieval Serlo Roger de Wynkleigh William de Stanwey Roger de Toriz John Noble Joh...

Gagak hutan Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Passeriformes Famili: Corvidae Genus: Corvus Spesies: C. enca Nama binomial Corvus enca(Horsfield, 1822) Sinonim Corvus violaceus Gagak hutan (bahasa Latin: Corvus enca) adalah spesies burung dari keluarga Corvidae, dari genus Corvus. Burung ini merupakan jenis burung pemakan buah lembut, mengkudu, Ficus, pepaya, kumbang, serangga, kada yang m...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chudadhuj Dharadilok – news · newspapers · books · scholar · JSTOR (February 2009) (Learn how and when to remove this template message) Prince of Phetchabun Chudadhuj DharadilokจุฑาธุชธราดิลกPrince of PhetchabunBorn(1892-07-04)4 July 1892Sichang Islan...
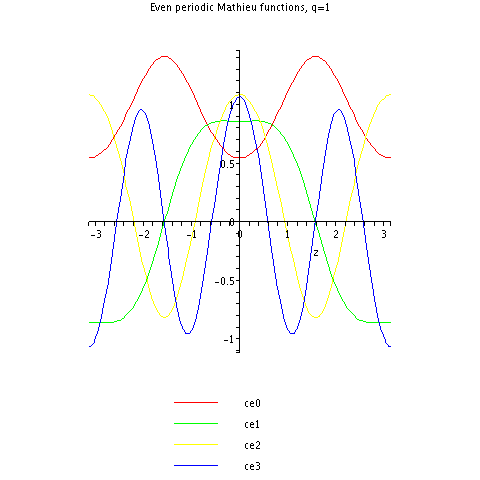
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (August 2018) (Learn how and when to remove this template message) The quantum pendulum is fundamental in understanding hindered internal rotations in chemistry, quantum features of scattering atoms, as well as numerous other quantum phenomena. Though a pendulum not subject t...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ghostwriter book series – news · newspapers · books · scholar · JSTOR (September 2018) (Learn how and when to remove this template message) One of the Ghostwriter books As with many television shows, Ghostwriter[1][circular reference] (4 Oc...

Spiced dried beef Pastirma Pastirma or basturma,[1] also called pastarma,[2] pastourma,[3] basdirma,[4] or basterma,[5] is a highly seasoned, air-dried cured beef that is found in the cuisines of Turkey, Armenia, Lebanon, the Levant, Azerbaijan, Bulgaria, Egypt, and Greece,[6][7][8][9] Iraq, and North Macedonia. Etymology and history Pastırma is mentioned in Mahmud of Kashgar's Diwan Lughat al-Turk and Evliya Çelebi...

Miranda del Castañar municipio de EspañaBanderaEscudo Vista general de la localidad Miranda del CastañarUbicación de Miranda del Castañar en España. Miranda del CastañarUbicación de Miranda del Castañar en la provincia de Salamanca. Mapa interactivo — Miranda del CastañarPaís España• Com. autónoma Castilla y León• Provincia Salamanca• Comarca Sierra de Francia• Partido judicial Béjar• Mancomuni...

Bilateral relationsIsrael–Lebanon relations Israel Lebanon Israel–Lebanon relations have experienced ups and downs since their establishment in the 1940s. Lebanon did take part in the 1948 Arab–Israeli War against Israel, but Lebanon was the first Arab League nation to signal a desire for an armistice treaty with Israel in 1949. Lebanon did not participate in the Six-Day War in 1967, nor the Yom Kippur War in 1973 in any significant way, and until the early 1970s, Lebanon's border with ...

Book by Katherine Addison The Angel of the Crows First editionAuthorKatherine AddisonCountryUnited StatesLanguageEnglishGenreFantasyPublishedJune 23, 2020PublisherTor BooksPages448ISBN978-0765387394 (hardcover 1st ed)OCLC1159883677 The Angel of the Crows is a 2020 fantasy novel written by the American author Sarah Monette under the pseudonym Katherine Addison. It is set in an alternate 19th century London, with supernatural creatures such as angels and is based on the Sherlock Holmes stories....

Academic journalFeminist TheologyDisciplineTheologyLanguageEnglishEdited byLisa Isherwood, Lillalou Hughes, Beverley ClackPublication detailsHistory1992 -presentPublisherSAGE PublicationsFrequencyTri-annuallyImpact factor(2010)Standard abbreviationsISO 4 (alt) · Bluebook (alt1 · alt2)NLM (alt) · MathSciNet (alt )ISO 4Fem. Theol.IndexingCODEN (alt · alt2) · JSTOR (alt) · LCCN (alt)MIAR · NLM ...







