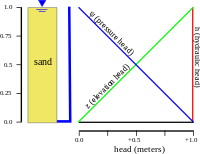
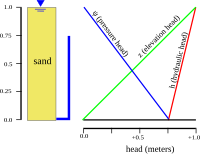
Hydraulic head
|
Read other articles:

Gładki Wierch Hladký štít Blick von dem Gipfel Świstowa Czuba, Bergseen Przedni Staw Polski und Wielki Staw Polski im Vordergrund Höhe 2065 m n.p.m. Lage Polen/Slowakei Gebirge Hohe Tatra, Karpaten Koordinaten 49° 12′ 26″ N, 20° 0′ 47″ O49.20722222222220.0130555555562065Koordinaten: 49° 12′ 26″ N, 20° 0′ 47″ O Gładki Wierch (Kleinpolen) Typ Felsgipfel Erstbesteigung 5. August 1902 durch Teodor Eic...

تفجير ملهى ليلي في برلين الغربية 1986 المعلومات البلد ألمانيا الإحداثيات 52°28′23″N 13°20′12″E / 52.473055555556°N 13.336666666667°E / 52.473055555556; 13.336666666667 التاريخ 5 أبريل 1986 الأسلحة عبوة ناسفة الخسائر الوفيات 3 الإصابات 231 تعديل مصدري - تعديل تفجير ملهى ليلي في ب

この項目では、全日本鉄道労働組合総連合会(JR総連)に所属し略称をJR北海道労組とする組合について説明しています。日本鉄道労働組合連合会(JR連合)に加盟し略称をJR北労組とする組合については「JR北海道労働組合」をご覧ください。 北海道旅客鉄道労働組合(JR北海道労組)設立年月日 1987年(昭和62年)2月前身組織 鉄道労働組合・国鉄動力車労働組合など組織

Power of the pope to depose monarchs Papal primacy, supremacy and infallibility Overview Primacy of Peter & Papal primacy Papal supremacy Papal infallibility First Vatican Council § Papal infallibility Patriarchscompared to popes Papal primacy Episcopal see § Catholic Church Apiarius of Sicca § Appeal to the bishop of Rome Pentarchy § After the East–West Schism Pope John XIX § Life Gregory II Youssef § First Vatican Council Ravenna Document Eastern Orthodox oppositionto papal supr...

Public university in Taipei, Taiwan Not to be confused with National Taiwan University of Science and Technology. National Taipei University of Technology國立臺北科技大學Former namesNational Taipei Institute of Technology (1994 - 1997)Motto誠、樸、精、勤[1]sêng, phok, cheng, khînMotto in EnglishIntegrity, Humbleness, Proficient, DiligenceTypePublicEstablished1912PresidentSea-Fue Wang[2]Academic staff451Students10,700Location1, Sec. 3, Zhongxiao E. Rd., Da...

Katedral IpialesKatedral Santo Petrus MartirKatedral IpialesLokasiIpialesNegara KolombiaDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupanKeuskupan Ipiales Katedral Ipiales atau yang bernama resmi Katedral Santo Petrus Martir adalah sebuah gereja katedral Katolik yang terletak di Ipiales, Kolombia. Katedral ini merupakan pusat kedudukan dan takhta bagi Keuskupan Ipiales.[1] Lihat juga Keuskupan Ipiales Gereja Katolik Roma Gereja Katol...

نيكولاي ميخائيلوفتش كرامزين (بالروسية: Николай Михайлович Карамзин) لوحة لكرامزين من طرف فاسيلي طروبينين, رسمت عام 1818 معلومات شخصية الميلاد 1 ديسمبر 1766[1][2][3][4] الوفاة 22 مايو 1826 (59 سنة) [5][1][2][6] سانت بطرسبرغ[7][8] مكان الد�...

The 3rd Earl with his sons George and Alexander George Seton, 3rd Earl of Winton (December 1584 – 17 December 1650) was a notable Royalist and Cavalier, the second son of Robert Seton, 1st Earl of Winton and 6th Lord Seton, by his spouse Margaret, daughter of Hugh Montgomerie, 3rd Earl of Eglinton. Biography Seton was known, before his older brother's illness as George Seton of St Germans. His Catholic tutor Stephen Ballantyne was criticised by the Presbytery of Tranent and the elders of Ha...

Alejandro Sanz is the artist with more entries in the list, with Más, El Alma al Aire, Viviendo Deprisa, 3 and No Es lo Mismo. This is a list of the best-selling albums in Spain that have been certified by the Productores de Música de España (PROMUSICAE). PROMUSICAE is in charge of certifying records in Spain. Until October 2005, the certification levels for albums in Spain were 50,000 for Gold and 100,000 for Platinum. The current levels, however, are 20,000 for Gold and 40,000 for Platin...

Metal Gear Solid V: Ground Zeroes Разработчик Kojima Productions Издатель Konami Локализатор СофтКлаб Часть серии Metal Gear Дата выпуска PlayStation 3, Xbox 360, PlayStation 4, Xbox One 18 марта 2014 20 марта 2014Microsoft Windows 18 декабря 2014 Жанр стелс-экшен Создатели Руководитель Хидэо Кодзима[1] Продюсеры Хидэо КодзимаКэнъитир�...

Polish poet and Nobel laureate (1923–2012) Wisława SzymborskaSzymborska in Kraków, 2009BornMaria Wisława Anna Szymborska(1923-07-02)2 July 1923Prowent, Poznań Voivodeship, PolandDied1 February 2012(2012-02-01) (aged 88)Kraków, PolandOccupationPoetessayisttranslatorNotable awards Goethe Prize (1991) Herder Prize (1995) Nobel Prize in Literature (1996) Order of the White Eagle (2011) Signature Maria Wisława Anna Szymborska[1][2] (Polish: [viˈswava ʂɨmˈbɔrsk...

Capital intelectual é o conjunto de conhecimentos e informações, ou seja, a soma do capital humano e o capital estrutural.[1] Pode ser definido como seres humanos. Esses conhecimentos podem ser tácitos - advindos das experiências ao longo da vida, ou explícitos - são estruturados, criptografados e armazenados, sendo possível sua transmissão a outras pessoas.[2] Conceito Representação do cérebro principal órgão e centro do sistema nervoso em todos os animais vertebrados. Filosofi...

Memorial to Chisholm and Ferguson, near Struy Mo rùn geal òg (My fair young love), alternately known as Cumha do dh'Uilleam Siseal (Lament for William Chisholm) is a Scottish Gaelic lament written by Christina Fergusson for her husband, William Chisholm of Strathglass, who was killed at the Battle of Culloden in 1746. Fergusson was possibly born in Contin, Ross-shire.[1][2] She was married to William Chisholm, who was a smith, armourer and standard bearer for the Chief of Cl...

Season of television series JustifiedSeason 5Season 5 DVD coverCountry of originUnited StatesNo. of episodes13ReleaseOriginal networkFXOriginal releaseJanuary 7 (2014-01-07) –April 8, 2014 (2014-04-08)Season chronology← PreviousSeason 4 Next →Season 6 List of episodes The fifth season of the American neo-Western[1] television series Justified premiered on January 7, 2014, on FX, and concluded on April 8, 2014, consisting of 13 episodes.[2] The se...

1984 Indian filmDhavani KanavugalPosterDirected byK. BhagyarajWritten byK. BhagyarajProduced byK. BhagyarajStarringK. BhagyarajRadhikaSivaji GanesanCinematographyA. V. RamakrishnanEdited byA. SelvanathanMusic byIlaiyaraajaProductioncompanyPraveena Film CircuitRelease date 14 September 1984 (1984-09-14) Running time148 minutesCountryIndiaLanguageTamil Dhavani Kanavugal (transl. Sweet Dreams) is a 1984 Indian Tamil-language drama film written, directed and produced by K. Bh...

American actress Julia NicksonNickson on the set of Around the World in 80 Days (1989)BornSingaporeOther namesJulia Nickson-SoulOccupationActressYears active1982–presentSpouse David Soul (m. 1987; div. 1993)ChildrenChina Soul Julia Nickson is a Singaporean–American actress. She first came to the attention of audiences in the United States in the Sylvester Stallone film Rambo: First Blood Part II. She appeared in the 2004 film E...

Jayalalithaa Información personalNombre en tamil ஜெ. ஜெயலலிதா Nacimiento 24 de febrero de 1948 Melukote (India) Fallecimiento 5 de diciembre de 2016 (68 años)Chennai (India) Causa de muerte Paro cardiorrespiratorio Nacionalidad India (1950-2016)Religión Hinduismo FamiliaPadres Jayaram Rangachar Veda Jayaram EducaciónEducada en Bishop Cotton Girls' SchoolStella Maris College Información profesionalOcupación Actriz de cine y política Área Actuación y política ...

この記事の主題はウィキペディアにおける独立記事作成の目安を満たしていないおそれがあります。目安に適合することを証明するために、記事の主題についての信頼できる二次資料を求めています。なお、適合することが証明できない場合には、記事は統合されるか、リダイレクトに置き換えられるか、さもなくば削除される可能性があります。出典検索?: 森とい...

Modernist movement of aesthetic in Nepal Nyatapola Temple located in Bhaktapur, Nepal, built in 1701–1702 CE The Great Drigung Kagyud Lotus Stupa in Lumbini, Nepal Traditional architecture of Kathmandu Nepali architecture or Nepalese architecture is a unique blend of artistic and practical considerations. Situated between the trade routes of India, Tibet and China, Nepali architecture reflects influences from these cultural strongholds. The pagoda architectural tradition figures prominently...

American baseball player (1934-2004) Baseball player Chuck HillerHiller in 1961Second basemanBorn: (1934-10-01)October 1, 1934Johnsburg, Illinois, U.S.Died: October 20, 2004(2004-10-20) (aged 70)St. Pete Beach, Florida, U.S.Batted: LeftThrew: RightMLB debutApril 11, 1961, for the San Francisco GiantsLast MLB appearanceJune 2, 1968, for the Pittsburgh PiratesMLB statisticsBatting average.243Home runs20Runs batted in152 Teams San Francisco Giants (1961–1965)...