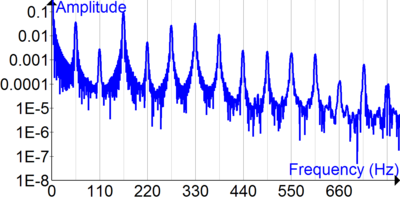
Harmonic analysis
|
Read other articles:

Harlan Page SanbornBiographical detailsBornNovember 11, 1889DiedSeptember 2, 1948Alma materDartmouth CollegeCoaching career (HC unless noted)1916–1917Virginia Tech1925–1926North Carolina Head coaching recordOverall37–7Accomplishments and honorsChampionships1 Southern Conference regular season (1926)1 Southern Conference Tournament (1926) Harlan P. Sanborn (1889-1948) was best known for being the head coach of the Virginia Tech Hokies men's basketball team and the North Carolina Tar...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Abril de 2020) Governadoria-geral de IrkutskGeografiaPaís Império RussoSede IrkutskFuncionamentoEstatuto entidade territorial administrativaGovernadoria-geral (Império Russo)HistóriaFundação 2 de junho de 1887Substitui Governad...

Удари по об'єктах критичної інфраструктури України під час російсько-української війниповітряна війна над Україною Відсутність світла вночі після масованих ударів проти об'єктів критичної інфраструктури України добре помітна з супутника NASA, 24 листопада 2022 рокуМісце

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2021) مالطا بيند الإحداثيات 39°11′39″N 93°21′43″W / 39.19417°N 93.36194°W / 39.19417; -93.36194 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى م

Vlaams Belang Jongeren Vlaams Belang Jongeren op een manifestatie tegen onverdoofd slachten Algemene gegevens Voorzitter Filip Brusselmans Actief in Vlaanderen België Hoofdkantoor Madouplein 8/6 1210 Brussel Ideologie · Geschiedenis Ideologie Vlaams-nationalismeConservatisme Oprichting 1987 Verwante organisaties Moederpartij Vlaams Belang Europese organisatie YEAH Media Ledenblad Rebel![1] Breuklijn[2] Website www.vbj.org Portaal Politiek Vlaams Belang Jongeren ...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Suku Dayak – berita · surat kabar · buku · cendekiawan · JSTOR Suku Dayak J.C.Oevaang Oeray Tjilik Riwut Stephen Kalong Ningkan Agustin Teras Narang Henry Ewan Golding Daud Yordan Cornelis Pandelela Rinong Zi...

هو توهم الإنسان لحقيقة نفسه وإمكانياته وظروفة علي نحو يخالف الواقع ولكن يتفق مع هواه ورغبته والفرد بطبيعة الحال لا يكون متعمدا ذلك بل إنه يقوم بخداع نفسه دون وعي بذلك كأن تكون إمكاناتة العقلية والعلمية ضعيفة ويري هو عكس ذلك يقول الفيلسوف الأميركي مايكل نوفاك لا حدود معروفة

NBC affiliate in Columbus, Ohio This article is about the television station which formerly used the WLWC callsign. For the television station in Providence, Rhode Island that currently uses that callsign, see WLWC. WCMH-TVColumbus, OhioUnited StatesChannelsDigital: 14 (UHF)Virtual: 4BrandingNBC 4ProgrammingAffiliations4.1: NBCfor others, see § SubchannelsOwnershipOwnerNexstar Media Group(Nexstar Media Inc.)HistoryFoundedNovember 1946[citation needed]First air dateApril 3, ...

Difficulty in learning or comprehending arithmetic Medical conditionDyscalculiaPronunciation/ˌdɪskælˈkjuːliə/ SpecialtyPsychiatryComplicationsdifficulty with daily tasksDurationLifetime Dyscalculia (/ˌdɪskælˈkjuːliə/)[1][2][3][4] is a disability resulting in difficulty learning or comprehending arithmetic, such as difficulty in understanding numbers, learning how to manipulate numbers, performing mathematical calculations, and learning facts in...

At the 1906 Summer Olympics in Athens, a tug of war event was contested.[1] Now called the Intercalated Games, the 1906 Games are no longer considered as an official Olympic Games by the International Olympic Committee. Medal summary Event Gold Silver Bronze Tug of war Germany (GER)Karl KaltenbachJosef KrämerHeinrich RondiWilhelm Dörr Wilhelm RitzenhoffJulius WagnerHeinrich SchneidereitWilhelm Born Greece (GRE)Spyros LazarosAntonios Tsitas Spyros VellasVassilio...

Angkatan BersenjataKekaisaran Romawi Timur Daftar artikel di bawah ini adalah bagian dari seri tentang angkatan bersenjata (militer dan paramiliter) Kekaisaran Romawi Timur, 330–1453 M Sejarah organisasi Angkatan Darat Klasik themata tagmata Hetaireia AD masa Komnenos pronoia) AD masa Palaiologos allagia Penjaga Varangia Jenderal Magister militum Domestikos ton skholon Megas Domestikos Stratopedarkhes Protostrator Angkatan Laut Romawi Timur: Api Yunani Dromon Laksamana (Droungarios Megas do...

Nok Airนกแอร์ IATA ICAO Kode panggil DD NOK NOK AIR Didirikan10 Februari 2004Mulai beroperasi23 Juli 2004PenghubungBangkok-Don MueangChiang MaiPhuketAliansiValue AllianceArmada33Tujuan36SloganSmiling Across AsiaPerusahaan indukNok Airlines Public Company LimitedKantor pusatBangkok, ThailandTokoh utamaDr Wutthiphum Jurangkool (CEO)Situs webhttp://www.nokair.com Nok Air (Bahasa Thai: นกแอร์) adalah maskapai penerbangan bertarif rendah yang berpusat di Bangkok, Thailand. ...

Serbian handball club RK JugovićFull nameRukometni Klub JugovićNickname(s)Kaćki tići (The Kać's Fledglings)Founded1956; 67 years ago (1956)ArenaHram Sport Hall, KaćCapacity2,000Head coachPredrag TopićLeagueArkus LigaClub colours Home Away Website Official site RK Jugović (Serbian Cyrillic: РК Југовић) is a Serbian handball club based in Kać, Novi Sad. They compete in the top tier Serbian handball league, the Arkus league. Kaćcla...

Hubungan Kuba-Israel Kuba Israel Hubungan Kuba–Israel merujuk kepada hubungan sejarah dan saat ini antara Kuba dan Israel. Kedua negara tersebut tak memiliki hubungan diplomatik resmi sejak 1973. Israel menempatkan Seksi Kepentingan di kedubes Kanada di Havana.[1] Sejarah Hubungan awal Duta Besar Kuba Ricardo Wolf dengan Presiden Israel Yitzhak Ben-Zvi adan Menteri Luar Negeri Golda Meir di Yerusalem, 1960 Sejak pendirian Israel, hubungan antara Kuba dan Israel merenggang. Pada 1919...

Pycnoporellus fulgens, an old spruce forest indicator polypore In Finland, Kotiranta and Niemelä (1993,[1] 1996[2]) introduced a widely used method for comparing the conservation values of different forest areas, based on the observation that certain wood-rotting fungi are very sensitive to the impact of human activities on forest ecosystems. Such species are slow to return to areas from where they have disappeared, so their presence is evidence of a long continuity in forest...

2014 film HeartbeatFilm posterDirected byAndrea DorfmanWritten byAndrea DorfmanStarringTanya DavisCinematographyStéphanie Weber BironEdited byThorben BiegerMusic byTanya Davis, Charles AustinDistributed byMongrel MediaRelease date 6 September 2014 (2014-09-06) (TIFF) Running time93 minutesCountryCanadaLanguageEnglish Heartbeat is a 2014 Canadian drama film written and directed by Andrea Dorfman. It was screened in the Contemporary World Cinema section at the 2014 Toronto I...

Former railway and docks company in South Wales Crest of the Barry Railway Company The Barry Railway Company was a railway and docks company in South Wales, first incorporated as the Barry Dock and Railway Company in 1884. It arose out of frustration among Rhondda coal owners at congestion and high charges at Cardiff Docks as well the monopoly held by the Taff Vale Railway in transporting coal from the Rhondda. In addition, the Taff Vale did not have the required capacity for the mineral traf...

Species of insect Naupactus xanthographus Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Coleoptera Infraorder: Cucujiformia Family: Curculionidae Genus: Naupactus Species: N. xanthographus Binomial name Naupactus xanthographus(Germar, 1824) Naupactus xanthographus is a species of beetle of the family Curculionidae native to South America, well known for its predation to more than 45 species of fruit trees of agricultural importance...

Eastern Catholic territorial jurisdiction in Rome, Italy Territorial Abbacy of Saint Mary of GrottaferrataAbbatia Territorialis Beatissimæ Mariæ Cryptæferratæ [1]Santa Maria di GrottaferrataCathedral of Exarchial Monastery of St. Mary of GrottaferrataLocationCountryItalyEcclesiastical provinceHoly See[1]StatisticsParishes1Churches1Schools1Members87[2]InformationDenominationItalo-Albanian Catholic ChurchRiteByzantine RiteEstablished1937[1]CathedralExarchial ...

National association football team This article is about the men's team. For the women's team, see Panama women's national football team. PanamaNickname(s) Los Canaleros (The Canal Men) La Marea Roja (The Red Tide)AssociationFederación Panameña de FútbolConfederationCONCACAF (North America)Sub-confederationUNCAF (Central America)Head coachThomas ChristiansenCaptainAníbal GodoyMost capsGabriel Gómez (148)Top scorerLuis Tejada (43)Home stadiumEstadio Nacional Rommel Fernández GutiérrezFI...