Free variables and bound variables
|
Read other articles:

Dutch politician You can help expand this article with text translated from the corresponding article in Dutch. (July 2009) Click [show] for important translation instructions. View a machine-translated version of the Dutch article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the En...
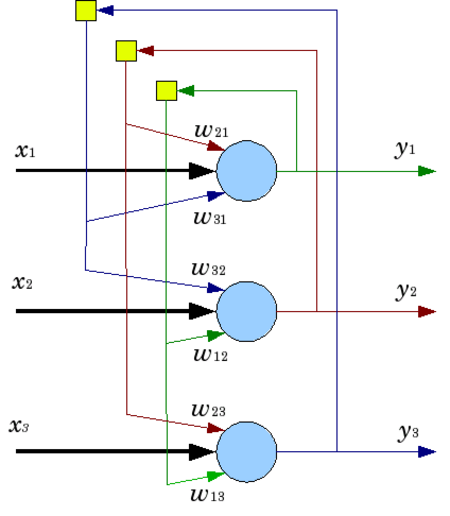
Нейро́нная сеть Хо́пфилда (англ. Hopfield network) — полносвязная нейронная сеть с симметричной матрицей связей. В процессе работы динамика таких сетей сходится (конвергирует) к одному из положений равновесия. Эти положения равновесия определяются заранее в процессе обуче

En este artículo se detectaron varios problemas. Por favor, edítalo y/o discute los problemas en la discusión para mejorarlo: Carece de fuentes o referencias que aparezcan en una fuente acreditada. Las referencias no son claras o tienen un formato incorrecto. Este aviso fue puesto el 16 de noviembre de 2023. Puedes avisar al redactor principal pegando lo siguiente en su página de discusión: {{sust:Aviso PA|Ley Lara|formato de referencias|referencias}} ~~~~ Ley Lara Pre...

Königswartha Castelo de Königswartha Brasão Mapa KönigswarthaMapa da Alemanha, posição de Königswartha acentuada Administração País Alemanha Estado Saxônia Região administrativa Dresden Distrito Bautzen Prefeito Swen Nowotny Partido no poder CDU Estatística Coordenadas geográficas 51° 18' 39 N 14° 18' 38 E Área 47,04 km² Altitude 141 m População 3.821[1] (31/12/2009) Densidade populacional 81,23 hab./km² Outras Informações Placa de veículo BZ Cód...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2021) دور السيداتمعلومات عامةالصنف الفني فيلم أكشن — فيلم وثائقي — فيلم رياضة تاريخ الصدور 2012 اللغة الأصلية الفرنسية — الولوفية البلد السنغالفرنسا الطاقمالمخ�...

У Вікіпедії є статті про інших людей із прізвищем Саенс Пенья. Роке Саенс Пенья ісп. Roque Sáenz Peña Del Sagrado Corazón de Jesús Роке Саенс ПеньяПрезидент Аргентини 12 жовтня 1910 — 9 серпня 1914Віцепрезидент Вікторіно де ла ПласаПопередник Хосе Фігероа АлькортаНаступник Вікторіно де л...

Resolusi 499Dewan Keamanan PBBMahkamah InternasionalTanggal21 Desember 1981Sidang no.2.321KodeS/RES/499 (Dokumen)TopikMahkamah InternasionalRingkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Britania Raya Amerika Serikat Uni SovietAnggota tidak tetap Spanyol Jerman Timur Irlandia Jepang Meksiko Niger Panama Filipina Tunisia Uganda...
Battle of the Anglo-Russian invasion of Holland Battle of KrabbendamPart of Anglo-Russian invasion of HollandDate10 September 1799LocationKrabbendam, The Netherlands52°49′00″N 4°46′12″E / 52.8167°N 4.7700°E / 52.8167; 4.7700Result British victoryBelligerents France Batavian Republic Great BritainCommanders and leaders Guillaume Marie Anne Brune Herman Willem Daendels Ralph AbercrombyStrength 25,000 23,000Casualties and losses 1,876 dead and wound...

Swiss handball player Lea Schüpbach Personal informationFull name Lea SchüpbachBorn (1997-09-10) 10 September 1997 (age 26)Winterthur, SwitzerlandNationality SwissHeight 1.78 m (5 ft 10 in)Playing position GoalkeeperClub informationCurrent club TuS MetzingenNumber 16Youth careerYears Team2010-2013 Yellow WinterthurSenior clubsYears Team2013-2017 Yellow Winterthur2017-2019 Spono Eagles2019-2020 Paris 922020-2022 HSG Bad Wildungen2022- TuS MetzingenNational teamYears Team ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. AcamarachiPiliTitik tertinggiKetinggian6.046 m (19.836 ft)Puncak1.608 m (5.276 ft)Masuk dalam daftarUltraKoordinat23°18′S 67°37′W / 23.300°S 67.617°W / -23.300; -67.617Koordinat: 23°18′S 67°37′W...

Gölpazarı Hilfe zu Wappen Gölpazarı (Türkei) Basisdaten Provinz (il): Bilecik Koordinaten: 40° 17′ N, 30° 19′ O40.28361111111130.315277777778540Koordinaten: 40° 17′ 1″ N, 30° 18′ 55″ O Höhe: 540 m Einwohner: 6.092[1] (2020) Telefonvorwahl: (+90) 228 Postleitzahl: 11 700 Kfz-Kennzeichen: 11 Struktur und Verwaltung (Stand: 2021) Bürgermeister: Hayri Suer (AKP) Postanschrift: Orta MahalleBakan Fatih Dönmez Cad...

Вибори Голови Європе́йського парла́менту 2017 року — це 15-те (з 1979 року) обрання Голови Європе́йського парла́менту депутатами Європейського парламенту, що проходило 17 січня 2017 року. Лише в четвертому турі таємним голосуванням було обрано представника групи Європейськ�...

Condiciones de iluminación en el polo sur de la luna. En color blanco, luz permanente; en color negro, sombra permanente (entre los 88° y los 90°) El término pico de luz eterna describe un punto en concreto de un cuerpo del Sistema Solar bañado constantemente por la luz del Sol. Esto es debido tanto a la rotación del cuerpo como a la altitud del punto en cuestión. La existencia de dichos puntos fue propuesta por primera vez por Camille Flammarion en 1879, quien especuló con la existen...

This article is about Ranks of the French Army. For more details about the naval ranks, see Ranks in the French Navy. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ranks in the French Army – news · newspapers · books · scholar · JSTOR (December 2017) (Learn how and when to remove this template message) Fre...

Promotion of fear of the rise of communism in Japan Part of a series onConservatism in Japan Ideologies Fiscal Nationalist Neo Populist Shōwa Statism State capitalism State Shinto Ultra Themes Anti-communism Asian values Authority Duty Elitism Familialism Filial piety Hierarchy Kokutai Law and order Loyalty Meritocracy Militarism Monarchism Patriotism Racism Social order Sovereignty Tradition Ultranationalism Intellectuals Etō Fukuda Hasuda Hirata Hyakuta Kanokogi Kobayashi Masaki May...

Telephone Wall telephone developed by Herrmann, part of the Communication Museum in Lisbon. The Herrmann wall telephone, also known as the privileged phone, was a type of telephone, created by the Portuguese inventor, Maximiliano Augusto Herrmann, in 1880. The pioneering use of buttons to activate the telephone played a fundamental role to the opening of public lines in the main cities of Portugal.[1] The telephone was composed by a double earpiece, made with long flexible tubes, and ...

2019 single by Lady AntebellumWhat If I Never Get Over YouSingle by Lady Antebellumfrom the album Ocean ReleasedMay 17, 2019 (2019-05-17)RecordedMarch 4, 2019 (2019-03-04)StudioStarstruck Recording Studios (Nashville, Tennessee)GenreCountryLength3:26LabelBMLG RecordsSongwriter(s)Ryan HurdSam EllisLaura VeltzJon GreenProducer(s)Dann HuffLady Antebellum singles chronology Heart Break (2017) What If I Never Get Over You (2019) Ocean (2019) Music videoWhat If I Never...

Ethnic group of the Philippines IfugaoYoung Ifugao women in traditional attireTotal population82,718[1] (2020 census)Regions with significant populations Philippines (Cordillera Administrative Region)LanguagesIfugao, Ilocano, TagalogReligionChristianity, indigenous folk religionRelated ethnic groupsIgorot peoples The Ifugao people are the ethnic group inhabiting Ifugao province in the Philippines. They reside in the municipalities of Lagawe (capital of Ifugao), Aguinaldo, Alfonso...

Shopping mall in the Philippines SM City BaguioLocationBaguio, PhilippinesCoordinates16°24′32″N 120°35′57″E / 16.40882°N 120.59918°E / 16.40882; 120.59918AddressLuneta Hill, Upper Session RoadOpening dateNovember 21, 2003; 20 years ago (2003-11-21)DeveloperSM Prime HoldingsManagementSM Prime HoldingsOwnerHenry SyArchitectJose Siao Ling and AssociatesNo. of stores and services400+ (as of 2021)No. of anchor tenants10Total retail floor area17...

United States historic placeLagonda Club BuildingU.S. National Register of Historic Places Southern and eastern sides of the buildingShow map of OhioShow map of the United StatesLocationNorthwestern corner of High (US 40) and Spring Sts., Springfield, OhioCoordinates39°55′23.8″N 83°48′25.456″W / 39.923278°N 83.80707111°W / 39.923278; -83.80707111Arealess than 1 acre (0.40 ha)Built1895ArchitectFrank M. AndrewsArchitectural styleLate 19th and 20th C...







![{\displaystyle \forall x\ \exists y\ {\Big [}\varphi (x,y,z){\Big ]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47da17bce01d9a1eaf29a4b325a8d9e1be3c0c10)










![{\displaystyle f=\left[(x_{1},\ldots ,x_{n})\mapsto t\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c78390d95fb9418ce489934e88b608112587ee70)




