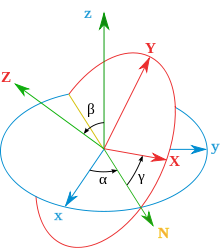
Angular velocity
| |||||||||||||||||||||||||||||||||||
Read other articles:

GyeongjuPoster teatrikalSutradaraZhang LuProduser Na Gyeong-chan Kim Dong-hyun Zhang Lu Ditulis oleh Zhang Lu PemeranPark Hae-il Shin Min-ahSinematograferCho Young-jikPenyuntingKim Hyeong-juDistributorInvent D (Korea Selatan)M-Line Distribution (seluruh dunia)Tanggal rilis 12 Juni 2014 (2014-06-12) Durasi149 menitNegara Korea Selatan Tiongkok Bahasa Korea Gyeongju (Hangul: 경주) adalah film komedi romantis Korea Selatan tahun 2014 yang ditulis dan disutradarai oleh Zhang Lu, d...

Species of snake Many-horned adder Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Reptilia Order: Squamata Suborder: Serpentes Family: Viperidae Genus: Bitis Species: B. cornuta Binomial name Bitis cornuta(Daudin, 1803) Synonyms[2] Vipera cornuta Daudin, 1803 Vip[era]. lophophris Cuvier, 1829 Vip[era]. lophophrys — Wagler, 1830 Vipera lophophris — Gray, 1831 Cerastes co...

De Grote Bosatlas, 50e editie 1988 De Dam Holwerd-Ameland in de Bosatlas van 1877 De Bosatlas is de overkoepelende naam voor een reeks Nederlandse atlassen. Deze atlassen behoren tot de meest gebruikte in het Nederlandse onderwijs. Vooral De Grote Bosatlas en De Kleine Bosatlas (ook wel De Basis Bosatlas geheten) zijn in Nederland bekend. Uitgaves ervan werden jarenlang verzorgd door Wolters Kluwer, die in 2007 de educatieve tak verkocht, waarbij werd bedongen dat dat de naam Wolters door de ...

Ne doit pas être confondu avec Music Hole (film). Cet article est une ébauche concernant un album. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Music Hole Album de Camille Sortie 7 avril 2008 Genre Chanson Label Virgin Music Albums de Camille Le Fil(2005) Ilo Veyou(2011)modifier Music Hole est le troisième album de Camille, sorti le 7 avril 2008. Il est écrit et produit en collaboration avec MaJi...

Ali Adil Shah ISultanBerkuasa1558–1579PendahuluIbrahim Adil Shah IPenerusIbrahim Adil Shah IIKematian1579[1]BijapurPemakamanAli Ka RouzaWangsaWangsa OsmanNama lengkapAbul Muzaffar Ali Adil ShahAyahIbrahim Adil Shah IIbuPutri dari Asad Khan Lari (Khusrow)AnakIbrahim Adil Shah II, putra angkat.AgamaSyiah Ali Adil Shah I (1558–1579) adalah Sultan kelima dari Kesultanan Bijapur. Pada hari pengangkatannya, Ali menyingkirkan praktik-praktik Sunni dan mengenalkan kembali Khutbah Syi’ah...

Johannes Diderik van der Waals Vật lý vật chất ngưng tụ Pha · Chuyển pha * QCP Trạng thái vật chấtChất rắn · Chất lỏng · Chất khí · Ngưng tụ Bose–Einstein · Khí Bose · Ngưng tụ Fermion · Khí Fermi · Chất lỏng Fermi · Siêu rắn · Siêu lỏng * Tinh thể thời gian Hiện ứng phaTham số thứ b�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2018) هوارد ماثيوز معلومات شخصية الميلاد 29 نوفمبر 1885(1885-11-29) الوفاة 9 فبراير 1963 (عن عمر ناهز 77 عاماً)أولدهام الطول 5 قدم 8 بوصة (1.73 م)[1][1] مركز الل

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Sumaryato KayatmoLahir23 November 1942SurakartaWarga negaraIndonesiaOrang tuaRaden Mas Soemaryato ayah Sumaryato Kayatmo lahir di Surakarta, Jawa Tengah pada tanggal 23 November 1942. Sumaryanto adalah anak kedua dari enam bersaudara. Riwayat pendidika...

この項目「メキシカーナ航空704便墜落事故」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。(原文:2022年10月20日時点の英語版記事) 修正、加筆に協力し、現在の表現をより自然な表現にして下さる方を求めています。ノートページや履歴も参照してください。(2023年2月) メキシ�...

American baseball player (born 1950) Baseball player Hank WebbPitcherBorn: (1950-05-21) May 21, 1950 (age 73)Copiague, New York, U.S.Batted: RightThrew: RightMLB debutSeptember 5, 1972, for the New York MetsLast MLB appearanceOctober 2, 1977, for the Los Angeles DodgersMLB statisticsWin–loss record7–9Earned run average4.31Strikeouts71 Teams New York Mets (1972–1976) Los Angeles Dodgers (1977) Henry Gaylon Matthew Webb (born May 21, 1950) is a former pi...

Ini adalah nama Batak Pakpak, marganya adalah Bancin. Makmur Syahputra BancinBupati Aceh Singkil ke-1Masa jabatan2007 – 15 Oktober 2011PresidenSusilo Bambang YudhoyonoGubernurIrwandi YusufWakilKhazaliPendahuluHasdaruddin (Pj.)PenggantiKhazaliMasa jabatan2000–2005PresidenAbdurrahman WahidMegawati SoekarnoputriSusilo Bambang YudhoyonoGubernurAbdullah PutehAzwar Abubakar (Pj.)WakilMuadz VohryPendahuluTidak ada, jabatan baruPenggantiHasdaruddin (Pj.) Informasi pribadiLahir(1956-1...

1989 video gameCasino KidNorth American cover artDeveloper(s)SofelPublisher(s)SofelArtist(s)Tadao NomuraComposer(s)Toshio MuraiPlatform(s)NESReleaseJP: January 6, 1989NA: October 1989Genre(s)CasinoMode(s)Single-player Casino Kid is a casino video game for the Nintendo Entertainment System released in 1989. It was developed and published by Sofel. In Japan, the game was released as $1,000,000 Kid: Maboroshi no Teiou Hen (100万$キッド 幻の帝王編) and is based on the manga series $1,0...

Historic site in Merseyside, EnglandHill BarkFrontage of Hill BarkLocationFrankby, Wirral, Merseyside, EnglandCoordinates53°21′50″N 3°08′05″W / 53.3639°N 3.1346°W / 53.3639; -3.1346OS grid referenceSJ 244 858Built1891Built forRobert William HudsonRebuilt1928–31Restored byRees & HoltArchitectGrayson & OuldArchitectural style(s)VernacularGoverning bodyHillbark Hotel Listed Building – Grade II*Designated5 June 1963Reference no.1242748 Location...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Dezembro de 2021) Este artigo ou seção pode conter informações desatualizadas. Se tem conhecimento sobre o tema abordado, edite a página e inclua as informações mais recentes, citando fontes fiáveis e independentes. —Encontre fon...

Fictional Marvel Comics superhero For the Golden Age version of the Blue Marvel, see Marvel Boy (Robert Grayson). Comics character Blue MarvelArtwork from Age of Heroes #3.Depicting from left: King Hyperion vs. Blue Marvel.Art by M. C. Wyman.Publication informationPublisherMarvel ComicsFirst appearanceAdam: Legend of the Blue Marvel #1(November 2008)Created byKevin Grevioux (writer)Mat Broome (artist)In-story informationAlter egoAdam Bernard BrashearSpeciesHuman mutatePlace of originEarthTeam...

1992 studio album by Vanessa Paradis Vanessa ParadisStudio album by Vanessa ParadisReleased21 September 1992Recorded1992StudioWaterfront (Hoboken, New Jersey)LabelRemarkProducerLenny KravitzVanessa Paradis chronology Variations sur le même t'aime(1990) Vanessa Paradis(1992) Live(1994) Singles from Vanessa Paradis Be My BabyReleased: September 1992 Sunday MondaysReleased: January 1993 Natural HighReleased: May 1993 Just as Long as You Are ThereReleased: July 1993 Vanessa Paradis is the th...

Public university in London, England This article needs to be updated. Please help update this article to reflect recent events or newly available information. (March 2019) University of East LondonUniversity of East London Coat of ArmsMottoLatin: Scientia et votorum impletioMotto in EnglishKnowledge and the fulfilment of vowsTypePublicEstablished1898 – West Ham Technical Institute1952 – West Ham College of Technology1970 – North East London Polytechnic1989 – Polytechnic of East ...

1813 battle during the War of the Sixth Coalition Battle of the KatzbachPart of the German campaign of the Sixth CoalitionBattle of the Katzbach by Eduard KaempfferDate26 August 1813[1]Locationnear Liegnitz, Prussia51°06′17″N 16°05′57″E / 51.10472°N 16.09917°E / 51.10472; 16.09917Result Russo-Prussian victoryBelligerents Kingdom of Prussia Russian Empire French EmpireCommanders and leaders Gebhard von Blücher Ludwig Yorck Osten-Sacken Jacques ...

British landowner and politician Sir Richard Mill, 5th Baronet (c. 1689–1760) of Woolbeding House, Sussex was a British landowner and politician who sat in the House of Commons between 1721 and 1747. Woolbeding House Mill was the second son of Sir John Mill, 3rd Baronet of Woolbeding and his wife Margaret Grey, daughter. of Thomas Grey of Woolbeding. He succeeded his brother John in the baronetcy in 1706 [1] He matriculated at St John's College, Oxford on 12 March 1708, aged 18.[...

Teesside trolleybus systemA Teesside trolleybus passing Dorman Long's Cleveland Iron Works, South Bank, Middlesbrough, July 1970OperationLocaleTeesside, North East EnglandOpen8 November 1919 (1919-11-08)Close18 April 1971 (1971-04-18)StatusClosedRoutes3Operator(s)Tees-side Railless Traction BoardInfrastructureElectrification550 V DCStock21 (maximum)StatisticsRoute length9.2 mi (14.8 km) The Teesside trolleybus system once served the conurbation of Teess...