Satz von Easton
|
Read other articles:

V6AsalJepangGenreJ-pop RockTahun aktif1995–2021LabelAvex EntertainmentSitus webSitus web V6 di Avex EntertainmentAnggotaMasayuki SakamotoHiroshi NaganoYoshihiko InoharaGo MoritaKen MiyakeJunichi Okada V6 adalah grup idola Jepang yang dibentuk oleh Johnny & Associates. Grup idola ini terdiri dari 6 orang pria. Singel pertama mereka, Music for the People dirilis pada 1 November 1995. V6 pernah memiliki acara televisi reguler yang diberi judul Gakkou e ikou (学校へ行こうcode: ja is d...

Владимир Сельков Личная информация Пол мужской Полное имя Владимир Владимирович Сельков Страна Россия Специализация плавание Клуб ЦСКА Волгоград Дата рождения 1 апреля 1971(1971-04-01) (52 года) Место рождения Березники, Пермская область, РСФСР, СССР Рост 188 см Вес 75 кг Наград...

1998 box set by Iron MaidenEddie's HeadBox set by Iron MaidenReleased1 December 1998LabelRaw Power RecordsIron Maiden box sets chronology The First Ten Years(1990) Eddie's Head(1998) Eddie's Archive(2002) Professional ratingsReview scoresSourceRatingAllMusic[1] Eddie's Head is a box set by Iron Maiden, in the shape of the head of their mascot, Eddie and containing their first 12 albums remastered, from Iron Maiden to Live at Donington, each with bonus multimedia material, plus...

Moos-Nabelmiere Moos-Nabelmiere (Moehringia muscosa) Systematik Kerneudikotyledonen Ordnung: Nelkenartige (Caryophyllales) Familie: Nelkengewächse (Caryophyllaceae) Unterfamilie: Alsinoidae Gattung: Nabelmieren (Moehringia) Art: Moos-Nabelmiere Wissenschaftlicher Name Moehringia muscosa L. Habitus am natürlichen Standort im Grazer Bergland Die Moos-Nabelmiere (Moehringia muscosa), auch Moosmiere genannt, ist eine der wenigen Pflanzen aus der Familie der Nelkengewächse (Caryophyllaceae) mit...

Bagian dari serial tentangBiologi evolusionerDiagram yang merepresentasikan divergensi kelompok taksonomi modern dari nenek moyang bersama mereka. Topik utama Pengenalan evolusi Nenek moyang bersama Bukti nenek moyang bersama Proses dan keluaran Genetika populasi Variasi Mutasi Seleksi alam Adaptasi Polimorfisme Hanyutan genetik Aliran gen Spesiasi Radiasi adaptif Kerjasama Koevolusi Divergen Konvergen Evolusi paralel Kepunahan Sejarah alam Asal mula Kehidupan Sejarah kehidupan Rentang waktu ...

توم برنس معلومات شخصية الميلاد 13 أغسطس 1964 (59 سنة) كانكاكي مواطنة الولايات المتحدة الحياة العملية المهنة لاعب كرة قاعدة الرياضة كرة القاعدة تعديل مصدري - تعديل توم برنس (بالإنجليزية: Tom Prince) هو لاعب كرة قاعدة أمريكي، ولد في 13 أغسطس 1964 في كانكاكي في الول

5th episode of the 34th season of The Simpsons Not ItThe Simpsons episodeEpisode no.Season 34Episode 5Directed bySteven Dean MooreWritten byCesar MazariegosProduction codeUABF17Original air dateOctober 23, 2022 (2022-10-23)Episode chronology ← PreviousThe King of Nice Next →Treehouse of Horror XXXIII The Simpsons (season 34)List of episodes Not It (titled onscreen as Treehouse of Horror Presents: Not It) is the fifth episode of the 34th season of the American...

American labor leader Harold A. Schaitberger9th General President of the International Association of Fire FightersIn office2000–2021Preceded byAlfred K. WhiteheadSucceeded byEdward Kelly This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find so...

Alan FreedLahirAlbert James Freed(1921-12-15)15 Desember 1921Windber, Pennsylvania, ASMeninggal20 Januari 1965(1965-01-20) (umur 43)Palm Springs, California, ASMakamLake View CemeteryPekerjaanDisjokiTahun aktif1945–65Suami/istriBetty Lou Bean (m. 1943; c. 1949) Marjorie J. Hess (m. 1950; c. 1958) Inga Lil Boling (m. 1959; his death 1965&#...

Japanese manga series Monster Hunter OrageMonster Hunter Orage art of mangaモンスターハンター オラージュ(Monsutā Hantā Orāju)GenreAdventure, fantasy[1] MangaWritten byHiro MashimaPublished byKodanshaEnglish publisherNA: Kodansha USAMagazineMonthly Shōnen RivalDemographicShōnenOriginal runApril 4, 2008 – May 2, 2009Volumes4 (List of volumes) Monster Hunter Orage (Japanese: モンスターハンター オラージュ, Hepburn: Monsutā Hantā Orāju) is a ...
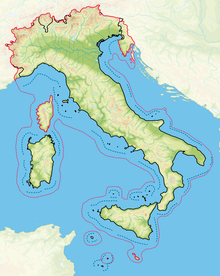
Las fronteras de la República Italiana en negro, las fronteras de la región geográfica italiana en rojo. Italia es una región geográfica de Europa del Sur con una superficie de 324 000 km²; delimitada al noroeste, al norte y al noreste por los Alpes y en sus restantes lados por el mar Mediterráneo.[1] Esta región se corresponde con los territorios de Italia, San Marino, Vaticano, Mónaco y Malta, a los cuales se pueden añadir porciones de Francia, Suiza, Eslovenia y ...

King of Scots from 1249 to 1286 Alexander IIICoronation of King Alexander on Moot Hill, Scone. He is being greeted by the ollamh rígh, the royal poet, who is addressing him with the proclamation Benach De Re Albanne (= Beannachd Dé Rígh Alban, God Bless the King of Scotland); the poet goes on to recite Alexander's genealogy. By Alexander's side is Maol Choluim II, Earl of Fife, holding the sword.King of ScotsReign6 July 1249 – 19 March 1286Coronation13 July 1249PredecessorAlexander IISuc...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Death Domination – news · newspapers · books · scholar · JSTOR (November 2018) (Learn how and when to remove this template me...

In this Chinese name, the family name is Yu. Yu Xiusong (Chinese: 俞秀松) (1899 – February 21, 1939) was an early member of the Chinese Communist Party. He was born in Zhuji, Zhejiang. He started attending the Zhejiang First Normal School (currently Hangzhou High School) in 1916. The May 4 movement of 1919 led him to be a student activist. In 1920, he founded the Communist Youth League of China and became its first leader. In 1922, he supported the Constitutional Protection Movement ...

Irish newspaper This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Wexford People – news · newspapers · books · scholar · JSTOR (February 2020) (Learn how and when to remove this template message) TypeWeekly newspaperFormatTabloidOwner(s)Independent News & MediaLanguageEnglishHeadquartersChanning House, Upp...

Material that imitates leather Pleather redirects here. For the Toadies album, see Pleather (album). An artificial leather bag strap, made from plastic Artificial leather, also called synthetic leather, is a material intended to substitute for leather in upholstery, clothing, footwear, and other uses where a leather-like finish is desired but the actual material is cost prohibitive or unsuitable, or for ethical concerns. Artificial leather is known under many names, including leatherette, imi...

Sala Grabado que aparece en Promptuarii Iconum Insigniorum (1533), obra de Guillaume Rouille (1518-1589)Información personalNombre en Biblical Hebrew שֶׁלַח Nacimiento 2290 A.C.Fallecimiento 1857 A.C.FamiliaPadres ArfaxadHijos EberFamiliares Anexo:Descendencia de Noé[editar datos en Wikidata] Sala, Salah o Shelah[1] es un personaje menor del Antiguo Testamento y la Torá, aunque también es mencionado en el Nuevo Testamento. Etimología En hebreo שֶׁלַח (She'laj...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Edapally royal family – news · newspapers · books · scholar · JSTOR (January 2011) (Learn how and when to remove this template message) Edappalli Rajas (Kings of Edappalli, known to the Portuguese as Repolim and to the Dutch as Repleim) were the rulers of the late medieval feuda...

Resolusi 571Dewan Keamanan PBBOperasi-operasi perbatasan Afrika SelatanTanggal20 September 1985Sidang no.2.607KodeS/RES/571 (Dokumen)TopikAngola-Afrika SelatanRingkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Britania Raya Amerika Serikat Uni SovietAnggota tidak tetap Australia Burkina Faso Denmark Mesir India Madagaskar Peru Thailand ...

Israeli singer-songwriter Ishay Riboישי ריבוBackground informationBornFebruary 3, 1989Marseille, FranceGenresContemporary Jewish religious music, piyyut, nigun, pizmonim, folk, rockInstrument(s) Vocals guitar Years active2007–presentWebsiteishayribo.comMusical artist Ishay Ribo (Hebrew: ישי ריבו, born February 3, 1989) is an Israeli singer-songwriter. A Sephardic Orthodox Jew, he has gained popularity in Israel among Haredi, national-religious, and secular Jewish audiences. He...



















