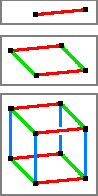
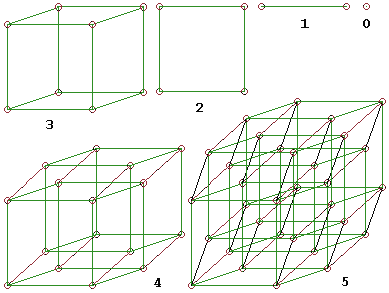
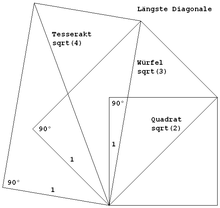
Hyperwürfel
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Taekwondo aux Jeux olympiques d'été de 2004 Généralités Sport Taekwondo Éditions 2e Lieu(x) Athènes Participants 124 Épreuves 8 Navigation Sydney 2000 Pékin 2008 modifier Aux Jeux olympiques de 2004, huit épreuves de taekwondo (quatre masculines et quatre féminines) voient 124 athlètes s'affronter. Elles se déroulent dans le Pavillon des sports du Complexe olympique de la zone côtière de Faliro. Tour préliminaire masculin au complexe olympique de Faliro. Tableau des médai...

List of wives of Joseph Smith See also: Origin of Latter Day Saint polygamy This article is part of a series onJoseph Smith 1805 to 1827 1827 to 1830 1831 to 1837 1838 to 1839 1839 to 1844 Death Legal Polygamy Wives Children Teachings Miracles Prophecies Bibliography Chronology Outline Category Latter Day Saints portalvte Joseph Smith (1805–1844), founder of the Latter Day Saint movement, taught and practiced polygamy during his ministry, and married multiple women during his life...

De Leeuwarderweg is een gedeelte van de Waterlandse Zeedijk ter hoogte van Tuindorp Buiksloot in Amsterdam-Noord. Het betreft een oude dijk, nu gelegen aan het huidige Volewijkspark en het toekomstige Noorderpark. Een aansluitende rijksstraatweg door de Buikslotermeer richting Broek in Waterland heette eerst ook Leeuwarderweg, maar na flinke aanpassingen in de jaren 60 kreeg deze weg de naam Nieuwe Leeuwarderweg. Leeuwarderweg gezien in noordelijke richtingIn 1935 werd de Leeuwarderweg aangel...

Das BoriS (eigentlich Berufswahl-SIEGEL Baden-Württemberg) ist eine Auszeichnung und Zertifizierung von Praxis-Projekten für Maßnahmen und Aktivitäten der Berufs- und Studienorientierung, die über die in den Bildungsplänen und den Verwaltungsvorschriften geforderten Standards weit hinausgehen. BoriS ist die Abkürzung für Berufsorientierung in Schulen.[1] Dabei muss es sich um bereits durchgeführte Maßnahmen im Sinne der Berufs- und Studienorientierung handeln. Logo mit Partn...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2022) الأجهزة الطبية ذات الاستخدام الواحد هي أي معدات أو أداوات أو أجهزة طبية يتحدد استخدامه لمرة واحدة فقط في المستشفى أو العيادة ويجب التخلص منه، تُعرِّف إدارة ا�...

?Чорна котяча акула носата Охоронний статус Даних недостатньо (МСОП 3.1) Біологічна класифікація Домен: Ядерні (Eukaryota) Царство: Тварини (Animalia) Підцарство: Справжні багатоклітинні (Eumetazoa) Тип: Хордові (Chordata) Підтип: Черепні (Craniata) Надклас: Щелепні (Gnathostomata) Клас: Хрящ

Львівське комунальне підприємство «Лев»ЛКП «Лев» ЛоготипСпеціалізація стерилізація безпритульних тваринГасло «Безпека львів'янам, захист тваринам»Засновник(и) Львівська міська радаШтаб-квартира Львів, вулиця Промислова, 56Територія діяльності ЛьвівПослуги стериліза

Borutta BorùtaKomuneComune di BoruttaLokasi Borutta di Provinsi SassariNegara ItaliaWilayah SardiniaProvinsiSassari (SS)Pemerintahan • Wali kotaSilvano Quirico Salvatore ArruLuas • Total4,76 km2 (1,84 sq mi)Ketinggian471 m (1,545 ft)Populasi (2016) • Total287[1]Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos07040Kode area telepon079Situs webhttp://www.comune.borutta.ss.it Borutta (bahasa ...

American businessman (1833–1892) This article is about the financier. For the lawyer and politician, see Robert Charles Winthrop. For the RN Admiral, see Robert Winthrop (1764–1832). Robert WinthropPainting of Winthrop by Chartran, c. 1880Born(1833-04-18)April 18, 1833DiedNovember 18, 1892(1892-11-18) (aged 59)New York CityResting placeGreen-Wood CemeteryBrooklyn, NYNationalityAmericanOccupationBankerSpouse Katherine Wilson Taylor (m. 1859)Child...

Film Titel We Refuse to DieLangtitel: Paramount Victory Short No. T2–2: We Refuseto Die Produktionsland USA Originalsprache Englisch Erscheinungsjahr 1942 Länge 14 Minuten Stab Regie William H. Pine Drehbuch Maxwell Shane Produktion William C. Thomas We Refuse to Die (Langtitel: Paramount Victory Short No. T2–2: We Refuse to Die) ist ein US-amerikanischer Dokumentarfilm aus dem Jahr 1942 unter der Regie von William H. Pine. Lidice nach der Zerstörung 1942 Bekanntmachung der deutsch...

1991 studio album by Kronos Quartet & Astor PiazzollaFive Tango SensationsStudio album by Kronos Quartet & Astor PiazzollaReleased25 January 1991 (1991-01-25)GenreContemporary classicalLength26:46LabelNonesuch (#79254)ProducerJudith ShermanKronos Quartet chronology Kevin Volans: Hunting:Gathering(1991) Five Tango Sensations(1991) Henryk Mikolaj Górecki: Already It Is Dusk/Lerchenmusik(1991) Five Tango Sensations is a suite of works (Asleep—Loving—Anxiety—Despertar�...

2015 Iranian docufiction film directed by Jafar Panahi TaxiOfficial poster for TaxiDirected byJafar PanahiWritten byJafar PanahiStory byJafar PanahiProduced byJafar PanahiStarringJafar Panahi Hana SaeidiCinematographyJafar PanahiEdited byJafar PanahiMusic byMossoumeh LahidjiProductioncompanyJafar Panahi Film ProductionsRelease date 6 February 2015 (2015-02-06) (Berlin) Running time82 minutesCountryIranLanguagePersianBox office$11.234.947[1] Taxi (full title Jafar Pa...

American singer-songwriter (1935–1980) For other people named Larry Williams, see Larry Williams (disambiguation). Larry WilliamsBackground informationBirth nameLawrence Eugene WilliamsBorn(1935-05-10)May 10, 1935New Orleans, Louisiana, United States[1]OriginNew OrleansDiedJanuary 7, 1980(1980-01-07) (aged 44)Los Angeles, California[1]Genres Rock and roll R&B funk soul Occupation(s)Singersongwritermusicianrecord producerInstrument(s)Vocals, pianoYears active1954–1...

1980 Canadian filmPhobiaTheatrical posterDirected byJohn HustonWritten byPeter BellwoodLew LehmanJimmy SangsterStory byRonald ShusettGary ShermanProduced byZale MagderStarringPaul Michael GlaserSusan HoganJohn ColicosCinematographyReginald H. MorrisEdited byStan ColeMusic byAndré GagnonDistributed byParamount PicturesRelease date September 9, 1980 (1980-09-09) Running time94 min. (approx.)CountryCanadaLanguageEnglishBudget$5,100,000Box office$59,167 Phobia is a 1980 Canadian h...

Grande Prêmio da Itáliade Fórmula 1 de 1985 50º GP da Itália realizado em Monza Detalhes da corrida Categoria Fórmula 1 Data 8 de setembro de 1985 Nome oficial LVI Gran Premio d'Italia[1][nota 1] Local Autódromo Nacional de Monza, Monza, Monza e Brianza, Lombardia, Itália Percurso 5.800 km Total 51 voltas / 295.800 km Condições do tempo Seco Pole Piloto Ayrton Senna Lotus-Renault Tempo 1:25.084 Volta mais rápida Piloto Nigel Mansell Williams-Honda Tempo 1:28.283 (na volta 38) Pódi...

Calendar year Millennium: 1st millennium BC Centuries: 3rd century BC 2nd century BC 1st century BC Decades: 130s BC 120s BC 110s BC 100s BC 90s BC Years: 116 BC 115 BC 114 BC 113 BC 112 BC 111 BC 110 BC 113 BC by topic Politics State leaders Political entities Categories Deaths vte 113 BC in various calendarsGregorian calendar113 BCCXII BCAb urbe condita641Ancient Egypt eraXXXIII dynasty, 211-...

NBC/CW affiliate in Dothan, Alabama WRGX-LD Dothan, AlabamaUnited StatesChannelsDigital: 23 (UHF)Virtual: 23BrandingWRGXDothan's CW (on LD2)Telemundo Dothan (on LD3)ProgrammingAffiliations23.1: NBC23.2: CW+23.3: TelemundoOwnershipOwnerGray Television(Gray Television Licensee, LLC)Sister stationsWTVY (TV)HistoryFirst air dateMay 2, 1990 (33 years ago) (1990-05-02)(original incarnation)June 1, 2013 (10 years ago) (2013-06-01)(current incarnation)Last air dateJanuary&...

Women's basketball team of the University of South Carolina South Carolina Gamecocks 2023–24 South Carolina Gamecocks women's basketball team UniversityUniversity of South CarolinaAll-time record982–535 (.647)Athletic directorRay TannerHead coachDawn Staley (16th season)ConferenceSECLocationColumbia, South CarolinaArenaColonial Life Arena (Capacity: 18,000)NicknameGamecocksColorsGarnet and black[1] Uniforms Home Away Alternate NCAA tournament champions20...

Chalki redirects here. For other places with the same name, see Chalki (disambiguation). Place in GreeceHalki ΧάλκηSatellite image of the islandHalkiLocation within the region Coordinates: 36°14′N 27°34′E / 36.233°N 27.567°E / 36.233; 27.567CountryGreeceAdministrative regionSouth AegeanRegional unitRhodesArea • Municipality37.04 km2 (14.30 sq mi)Highest elevation601 m (1,972 ft)Lowest elevation0 m (0 ...

Southwood Open Space is a 12.9 hectare Local Nature Reserve (LNR) in Old Malden in the Royal Borough of Kingston upon Thames in London. It is a linear park along the Hogsmill River between the Kingston Bypass opposite Elmbridge Avenue and the junction between the Hogsmill and a footpath to Manor Drive North.[1][2] The name Southwood Open Space is only used on the Natural England database of LNRs, and it is more commonly regarded as part of the Hogsmill River Park[3] or...