Grundlagen der Mathematik
|
Read other articles:

محمد رفيق طرار (بالأردوية: مُحمَّد رفیق تارڑ) مناصب رئيس المحكمة العليا في لاهور في المنصب6 مارس 1989 – 31 أكتوبر 1991 كبير قضاة المحكمة العليا الباكستانية في المنصب17 يناير 1991 – 1 نوفمبر 1994 عضو مجلس الشيوخ الباكستاني في المنصب1997 – 1998 رئيس باكست

Komorlar devlet başkanı, Afrika ada ülkesi Komorlar'ın bağımsızlığını kazandığı 1975 yılından bu yana ülkenin en üst makamında yer alan kişiye verilen unvandır. Ülke 1975 ile 1978 yılları arasında Komorlar Devleti, 1978 ile 2001 yılları arasında Federal Komorlar İslam Cumhuriyeti ve 2001 yılından itibaren de Komorlar Birliği olarak adlandırılmıştır. Ülkede devlet başkanı olarak görevde bulunan kişilerin listesi şu şekildedir: № Resim İsim(Doğum–

Stasiun Kai-Sumiyoshi甲斐住吉駅Stasiun JR Kai-Sumiyoshi, Januari 2006LokasiSumiyoshi 2-chome, Kōfu-shi, Yamanashi-kenJepangKoordinat35°38′11″N 138°34′11″E / 35.6363°N 138.5698°E / 35.6363; 138.5698Pengelola JR CentralJalur Jalur MinobuLetak dari pangkal83.1 kilometer dari FujiJumlah peron1 peron sampingInformasi lainStatusTanpa stafSejarahDibuka30 Maret 1928Penumpang2016498 per hari Lokasi pada petaStasiun Kai-SumiyoshiLokasi di Prefekfur YamanashiTam...

Mass Effect 2 Разработчик BioWare Издатель Electronic Arts Локализатор СофтКлаб Часть серии Mass Effect Дата анонса Xbox 360 и Windows 19 марта 2009[1] PlayStation 3 17 августа 2010[2] Даты выпуска 26 января 2010 Xbox 360 и Windows 26 января 2010 28 января 2010[3](ПК) 8 февраля 2010[4](Xbox 360) 29 января 2010[5] 13 января 2011[6...

此條目可参照德語維基百科相應條目来扩充。 (2020年3月15日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 此條目没有列出任何参考或来源。 (2020年3月15日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以

Поліна Да́шковаПолина Да́шкова Ім'я при народженні Тетяна Вікторівна ПоляченкоПсевдонім Поліна ДашковаНародилася 14 липня 1960(1960-07-14) (63 роки)м. Москва, РРФСР, СРСРГромадянство СРСР→ РосіяНаціональність росіянкаДіяльність Письменниця, поеткаAlma mater Літературний ін�...

Award ceremony for Spanish films of 1997 12th Goya AwardsDate31 January 1998SitePalacio Municipal de Congresos de MadridHosted byEl Gran WyomingHighlightsBest FilmLucky StarBest ActorAntonio ResinesLucky StarBest ActressCecilia RothMartín (Hache)Most awardsLucky Star (5)Most nominationsSecrets of the Heart (9)Television coverageNetworkTVE ← 11th Goya Awards 13th → The 12th Goya Awards were presented in Madrid, Spain on 31 January 1998.[1] The gala was hosted by ...

König Karl VIII. (Skulptur von Bernt Notke, heute in Schloss Gripsholm) Wappen Karls VIII. Grabstätte König Karls VIII. in der Riddarholmskyrkan Karl VIII. (Karl Knutsson Bonde, * 1408 oder 1409; † 15. Mai 1470) war Reichsverweser von Schweden von 1438 bis 1440 und dreimal König von Schweden und als Karl I. König von Norwegen von 1449 bis 1450. Er entstammte dem Geschlecht der Bonde und war der Sohn von Knut Tordsson Bonde und Margareta Karlsdotter (Sparre av Tofta). Nach dem frühen T...

Bolbitis lianhuachihensis Біологічна класифікація Царство: Рослини (Plantae) Клада: Судинні рослини (Tracheophyta) Відділ: Папоротеподібні (Polypodiophyta) Клас: Папоротевидні (Polypodiopsida) Порядок: Багатоніжкові (Polypodiales) Підпорядок: Polypodiineae Родина: Щитникові (Dryopteridaceae) Рід: Bolbitis Вид: B. lianhuachihensis Біноміаль

Wang FuzhiWang Fuzhi.Nama asal王夫之Lahir(1619-10-07)7 Oktober 1619Hengyang, Hunan, TiongkokMeninggal18 Februari 1692(1692-02-18) (umur 72)Hengyang, Hunan, TiongkokPekerjaanIlmuwan, filsufKarya terkenalChuanshan yishu quanjiGerakan politikSentimen anti-QingAnakWang Ban (putra)Wang Yu (putra)Orang tuaWang ZhaopingTan Ruren Wang Fuzhi Hanzi: 王夫之 Alih aksara Mandarin - Hanyu Pinyin: Wáng Fūzhī - Wade-Giles: Wang Fu-chih Zizhan Hanzi tradisional: 而農 Hanzi sederhana: 而�...

Albanian philologist and educator Aleksandër XhuvaniBorn(1880-03-14)14 March 1880Elbasan, Ottoman EmpireDied22 November 1961(1961-11-22) (aged 81)Tirana AlbaniaOccupationwriter, scholarNotable awards People's TeacherSignature Aleksandër Xhuvani (14 March 1880 – 22 November 1961) was an Albanian philologist and educator.[1] Xhuvani spent much of his career working for the improvement of Albanian schools; he also advocated the standardization of the Albanian language in the yea...

Indian singer/songwriter This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Afsana Khan – news · newspapers · books · scholar · JSTOR (March 2022) (Learn how and when to remove this template messag...

Manuel José Barrenechea Diputado de la República de Chilepor Taltal y Tocopilla 1915-1921 Información personalNombre completo Manuel José Barrenechea NaranjoNacimiento 23 de septiembre de 1857 Fallecimiento 19 de noviembre de 1929 (72 años)Nacionalidad ChilenaEducaciónEducado en Universidad de ChileInstituto NacionalColegio de los Sagrados Corazones de Santiago Información profesionalOcupación Médico, cirujano y político Partido político Radical[editar datos en Wikidata] ...

This article contains overly lengthy quotations. Please help summarize the quotations. Consider transferring direct quotations to Wikiquote or excerpts to Wikisource. (May 2022) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2022) (Learn how and when to remove this template message) Abel PolletBorn9 October 1873Vieux-Berquin, FranceDied11 January 1909Bé...

Australian pornographic film actress For other people named Angela White, see Angela White (disambiguation). Angela WhiteWhite in 2019BornSydney, New South Wales, Australia[1]Alma materUniversity of MelbourneOccupationPornographic actressAwardsFull list Angela Gabrielle White is an Australian pornographic film actress and director.[2] She has been inducted into the AVN Hall of Fame and the XRCO Hall of Fame, and in 2020 became AVN's first three-time Female Performer of th...
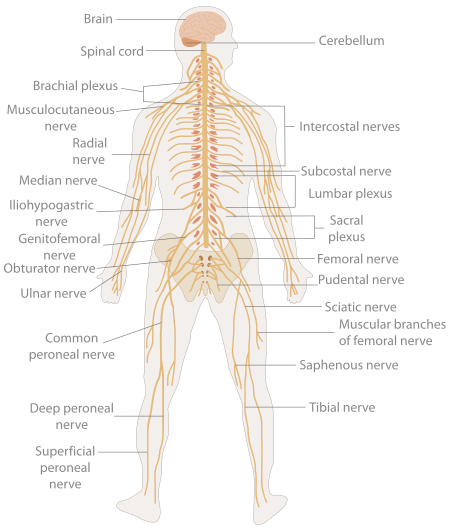
Group of organs assembled in a structural unit to serve a common function This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Organ system – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this template message) This article is part of a series on theDevelopment of organ sys...

1923 film This article is about the film. For the 2020 album by Kate Ceberano, Steve Kilbey and Sean Sennett, see The Dangerous Age (album). The Dangerous AgeCleo Madison and Lewis Stone in The Dangerous AgeDirected byJohn M. StahlScreenplay byJ.G. HawksBess MeredythLenore CoffeeStory byFrances Irene ReelsProduced byLouis B. MayerStarringLewis StoneCleo MadisonEdith RobertsRuth CliffordMyrtle StedmanJames MorrisonCinematographyJackson RoseAllen G. SieglerProductioncompanyLouis B. Mayer Produc...

Untuk film berjudul serupa tahun 1980, lihat Dilwale Dulhaniya Le Jayenge (film 1980). Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Dilwale Dulhania Le Jayenge di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemah...

Ancient Celtic tribe Castro de Castromao, Castro-capital of the Coelerni The Coelerni were an ancient Celtic tribe of Gallaecia in Hispania (the Iberian Peninsula), part of Calaician or Gallaeci people, living in what was to become the Roman Province of Hispania Tarraconensis, in what is now the southern part of the province of Ourense (in Galicia). Some sources, like Alarcão,[1] also state that the Coelerni lived in the north of modern Portugal, in the province of Trás-os-Montes, i...

منتخب منغوليا تحت 23 سنة لكرة القدم للرجال بلد الرياضة منغوليا الفئة كرة قدم تحت 23 سنة للرجال [لغات أخرى] مشاركات تعديل مصدري - تعديل منتخب منغوليا تحت 23 سنة للرجال لكرة القدم هو ممثل منغوليا الرسمي في المنافسات الدولية في كرة القدم في فئة كرة قدم تحت 23 سن�...
