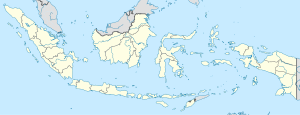
Gunung Gilap
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Chi-Chiチチ(Chichi)Fecha de nacimiento5 de noviembre, 737[1]Edad11-19 (Dragon Ball) 23-47 (Dragon Ball Z) 42-43 (Dragon Ball Super) 52 (Dragon Ball GT)Origen enMangaPrimera apariciónVolumen 1, capítulo 11 ChichiOtros nombresMilk (Hispanoamérica)Luchadora Anónima (23° Tenkaichi Budōkai)OcupacionPrincesa, ama de casa, artista marcial, cultivadora de rábanos, maestra de artes marcialesRelevanciaPersonaje secundarioProcedenciaTierraFamilia Gyūmaō (padre)Son Gokū (esposo)Son Goh...

Kevin Matthew Fertig Nacimiento Memphis, Tennessee, U.S.17 de enero de 1977 (46 años)[1]Nombres artísticos Kevin ThornKevin FertigVengeanceMordecaiSeven7evenSeven ThornPeso 122.5 kg (270 lb)Estatura 1,91 m (6′ 3″)[2]Nacionalidad Estados UnidosEntrenador Al Snow, Bill DeMott, Ivory, Nick DinsmoreEstadísticasDebut 2000[editar datos en Wikidata] Kevin Matthew Fertig (17 de enero de 1977) es un luchador profesional estadounidense, más conocido como K...

Grosir atau perkulakan (bahasa Inggris: wholesaling, distributing) diartikan sebagai penjualan barang atau barang niaga kepada pengecer, pengguna bisnis industri, komersial, institusi atau profesional, atau kepada pedagang besar/penggrosir lainnya dan jasa terkait.[1] Secara umum, artinya penjualan barang kepada siapa saja selain konsumen biasa. Grosir juga dapat didefinisikan sebagai penjualan barang dalam partai besar[2]. Biasanya, harga grosir diperuntukkan bagi transak...

Romanisches Medaillon im Mindener Domschatz Christliche Kunst, in der Kunstwissenschaft auch als Ars sacra (lat. für „heilige Kunst“) bezeichnet, umfasst im allgemeinen Sinn alle Bereiche künstlerischen Schaffens, die christliche Inhalte zum Thema haben, welche in verschiedenen Medien zum Ausdruck kommen – von der Musik über alle Bereiche der bildenden Kunst (insbesondere Malerei, Skulptur und Architektur) bis hin zur Kleinkunst (kirchliche Preziosen, Gerätschaften und Gewänder). I...

Unione di comuni Terre del Mare e del Soleunione di comuniLocalizzazioneStato Italia Regione Puglia Provincia Taranto AmministrazioneCapoluogoMaruggio PresidenteGiuseppe Fischetti Data di istituzione2001 TerritorioCoordinatedel capoluogo40°19′22″N 17°34′25″E / 40.322778°N 17.573611°E40.322778; 17.573611 (Unione di comuni Terre del Mare e del Sole)Coordinate: 40°19′22″N 17°34′25″E / 40.322778°N 17.573611°E40.322778; 17.573...

Sebuah pekan raya dagang untuk industri perjalanan Pekan raya adalah sebuah tempat pertemuan orang-orang untuk berbagai kegiatan hiburan atau komersial. Tempat tersebut biasanya berjangka waktu temporer yang berlangsung dari satu siang sampai beberapa pekan. Riwayat Pekan raya desa karya seniman Flemish Gillis Mostaert 1590 Pekan Raya Kuda, lukisan karya Rosa Bonheur (1852-1855) Pekan-pekan raya dijadikan hari libur pada zaman Romawi. Di provinsi-provinsi Yudea dan Syria Palaestina, para rabb...

Sifat ekstensif', seperti volume dan massa adalah sifat adiftif, dalam arti bahwa nilai sifat itu bagi keseluruhan benda adalah jumlah nilai-nilai dari semua bagian yang menjadikannya. Sifat ekstensif adalah sifat makroskopis yang bergantung pada massa atau kuantitas zat, contohnya massa, volume, mol, dan energi kinetik. dapat dikatakan bahwa sifat ekstensif merupakan sifat yang bergantung pada jumlah zat.[1] Dalam sifat ekstensif, nilai dari keseluruhan sistem merupakan penjumlahan n...

German mathematician (1885–1955) Weyl redirects here. For other persons, see Weyl (surname). Hermann WeylBornHermann Klaus Hugo Weyl(1885-11-09)9 November 1885Elmshorn, German EmpireDied8 December 1955(1955-12-08) (aged 70)Zürich, SwitzerlandAlma materUniversity of MunichUniversity of GöttingenKnown forList of topics named after Hermann WeylOntic structural realism[3]WormholeSpousesFriederike Bertha Helene Joseph (nickname Hella) (1893–1948)Ellen Bär (née Lohnst...

Indian State Government Government of OdishaSeat of GovernmentBhubaneswarWebsitewww.odisha.gov.inLegislative branchAssemblyOdisha Legislative AssemblySpeakerPramila Mallik (BJD)Deputy SpeakerSaluga Pradhan (BJD)Members in Assembly147Executive branchGovernorRaghubar DasChief MinisterNaveen Patnaik (BJD)Chief SecretaryShri Pradeep Kumar Jena, IASJudiciaryHigh CourtOrissa High CourtChief JusticeSubhasis Talapatra Secretariat of Odisha, Bhubaneswar. The government of the Indian state of Odisha an...

This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: phrasing, sentence structure, and WP:NOSOCIAL. Please help improve this article if you can. (October 2023) (Learn how and when to remove this template message)This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Music of Jordan – news �...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2017) (Learn how and when to remove this template message) This article needs additional citations for verification. Please help improve this article...

The Te of Piglet AuthorBenjamin HoffLanguageEnglishSubjectTaoism, PhilosophyPublisherDutton BooksPublication date1992Pages257ISBN0-525-93496-0OCLC25413491Dewey Decimal299/.514 20LC ClassPR6025.I65 Z69 1992Preceded byThe Tao of Pooh The Te of Piglet is a 1992 philosophical book written by Benjamin Hoff as a companion to his 1982 work The Tao of Pooh.[1] The book was published by Dutton Books and spent 21 weeks on the Publishers Weekly Bestseller List and 37 weeks on the...

2014 live-action animated comedy film by Paul King PaddingtonUK theatrical release posterDirected byPaul KingScreenplay byPaul KingStory by Hamish McColl Paul King Based onPaddington Bearby Michael BondProduced byDavid HeymanStarring Hugh Bonneville Sally Hawkins Julie Walters Jim Broadbent Peter Capaldi Nicole Kidman Ben Whishaw CinematographyErik WilsonEdited byMark EversonMusic byNick UrataProductioncompanies Heyday Films[1][2] StudioCanal[1] TF1 Films Production ...

1962 studio album by Art Farmer and Benny GolsonAnother Git TogetherStudio album by Art Farmer and Benny GolsonReleased1962RecordedMay 28 and June 21, 1962Nola's Penthouse Sound Studios, New York CityGenreJazzLength34:28LabelMercurySR 60737ProducerKay NortonArt Farmer chronology Here and Now(1962) Another Git Together(1962) Listen to Art Farmer and the Orchestra(1962) Benny Golson chronology Pop + Jazz = Swing(1962) Another Git Together(1962) Turning Point(1962) Another Git Together i...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Shinichi TeradaInformasi pribadiNama lengkap Shinichi TeradaTanggal lahir 10 Juni 1985 (umur 38)Tempat lahir Prefektur Osaka, JepangPosisi bermain GelandangKarier senior*Tahun Tim Tampil (Gol)2004-2012 Gamba Osaka 2010-2011 →Yokohama FC 2012- Yoko...

For the 2014 movie, see Tammy (film). For the Tammy movies of the 1950s and 1960s, see Tammy (film series). American TV series or program TammyStar of Tammy, Debbie WatsonGenreSitcomWritten byRobert V. BarronCid Ricketts SumnerDirected byLeslie GoodwinsSidney MillerStarringDebbie WatsonDenver PyleDonald WoodsDorothy GreenTheme music composerJay LivingstonRay EvansOpening themeTammyCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes26ProductionProducerDick...

Book by Leonard Eugene Dickson History of the Theory of Numbers Cover of the first editionAuthorL. E. DicksonCountryUnited StatesLanguageEnglishPublisherCarnegie Institution of WashingtonPublication date1919Media typePrint (hardback)PagesVol I: 486, Vol II: 803, Vol III: 313ISBN978-0-486-44232-7 (vol.1)ISBN 978-0-486-44233-4(vol.2)ISBN 978-0-486-44234-1(vol.3) By Chelsa publishing History of the Theory of Numbers is a three-volume work by Leonard Eugene Dickson summarizing work...

Era in the history of Calvinism For the Eastern Christian reformation movement, see Protestant Eastern Christianity. Reformed orthodoxy or Calvinist orthodoxy was an era in the history of Calvinism in the 16th to 18th centuries. Calvinist orthodoxy was paralleled by similar eras in Lutheranism and tridentine Roman Catholicism after the Counter-Reformation. Calvinist scholasticism or Reformed scholasticism was a theological method that gradually developed during the era of Calvinist Orthodoxy....

Government agency in Washington (state), United States This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (December 2022) Washington State Department of TransportationDepartment overviewFormedSeptember 21, 1977 (1977-09-21)[1]Preceding agenciesWashington State Department of HighwaysWashington State Aeronautics CommissionWashington State Toll Bridge AuthorityWashington State Canal Commi...

Pengamatan cincin serpihan Teleskop Angkasa Hubble di sekitar Fomalhaut. Tepi dalam piringan mungkin telah dibentuk oleh orbit Fomalhaut b, di kanan bawah. Piringan serpihan adalah sebuah piringan lingkar bintang berisi debu dan puing-puing yang mengorbit di sekitar bintang. Terkadang cakram tersebut berisi cincin menonjol, seperti yang terlihat pada gambar Fomalhaut di sebelah kanan. Piringan serpihan telah ditemukan di sekitar bintang dewasa dan bintang muda, serta setidaknya satu piringan ...