Прынцып нявызначанасці Гейзенберга
|
Read other articles:

Irene DunneLahirIrene Marie DunnPekerjaanAktrisTahun aktif1922–1962Suami/istriFrancis Dennis Griffin (1928–1965) Irene Dunne (20 Desember 1898 – 4 September 1990) merupakan seorang penyanyi dan aktris berkebangsaan Amerika Serikat yang memenangkan lima nominasi Academy Award. Dia dilahirkan di Louisville, Kentucky. Dia berkarier di dunia film sejak tahun 1930. Filmografi Leathernecking (1930) Cimarron (1931) The Slippery Pearls (1931) (short subject) Bachelor Apartmen...

Kanada Tim Horton Hockey Hall of Fame, 1977 Geburtsdatum 12. Januar 1930 Geburtsort Cochrane, Ontario, Kanada Todesdatum 21. Februar 1974 Sterbeort St. Catharines, Ontario, Kanada Größe 178 cm Gewicht 82 kg Position Verteidiger Schusshand Rechts Karrierestationen 1946–1947 Copper Cliff Junior Redmen 1947–1949 Toronto St. Michael’s Majors 1949–1952 Pittsburgh Hornets 1952–1970 Toronto Maple Leafs 1970–1971 New York Rangers 1971–1972 Pittsburgh Penguins 1972–1974 Bu...

American long jumper Albert GuttersonAlbert Gutterson at the 1912 OlympicsPersonal informationBornAugust 23, 1887Andover, Vermont, United StatesDiedApril 7, 1965 (aged 77)Burlington, Vermont, United StatesAlma materUniversity of VermontHeight1.85 m (6 ft 1 in)Weight82 kg (181 lb)SportSportAthleticsEventLong jumpClubBoston Athletic AssociationAchievements and titlesPersonal best7.60 m (1912)[1] Medal record Representing the United States Olympic Game...

Michal Šanda Michal Šanda (lahir 10 Desember 1965) ialah penulis Republik Ceko. Bibliografi stoa, (1994) Ošklivé příběhy z krásných slov, ISBN 80-85940-20-5, (1996) Metro, ISBN 80-85940-48-5, (1998, 2005) Dvacet deka ovaru, ISBN 80-86240-05-3, (1998) Blues 1890-1940, ISBN 80-7227-067-2, (2000) Obecní radní Stoklasné Lhoty vydraživší za 37 Kč vycpaného jezevce pro potřeby školního kabinetu, ISBN 80-7227-110-5, (2001) Sudamerická romance, ISBN 80-7227-164-4, (2003) Španělsk

2011 single by MisiaKiokuSingle by Misiafrom the album Soul Quest ReleasedMay 25, 2011 (2011-05-25)StudioRMT StudioBeethoven StudioEastcote StudiosAir StudiosGenreOrchestral popLength5:11LabelAriola JapanSongwriter(s)MisiaGorō MatsuiBZ4UProducer(s)Shirō SagisuMisia singles chronology Edge of This World (2010) Kioku (2011) Koi wa Owaranai Zutto (2012) Music videoKioku on YouTubeAudio sampleKiokufilehelp Kioku (記憶(きおく), lit. Memory, stylized as La Mémoire) is a s...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ștefăniță Lupu – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Ștefăniță LupuPrince of Moldavia(1st reign)Reign1 December 1659 – January 1661PredecessorConstantin ȘerbanSuccessorConstantin ȘerbanPrinc...

هذه المقالة عن وثيقة بيان السيرة المهنية. لجنس أدبي يصف فيه الكاتب حياته، طالع ترجمة ذاتية.سيرة ذاتيةمعلومات عامةصنف فرعي من مستند الاستعمال تطبيق[1] تلخيص[1] وصف في وصلة http://www.risorsedisumane.com/curriculum-vitae-in-formato-europeo/https://wirtschaftslexikon.gabler.de/definition/lebenslauf-41015 لديه جزء أو أجزا�...

English politician, diplomat and landowner His GraceThe Duke of SutherlandKG, PCAmbassador to FranceIn office1790–1792MonarchGeorge IIIPreceded byThe Duke of DorsetSucceeded byVacant Personal detailsBorn(1758-01-09)9 January 1758London, EnglandDied19 July 1833(1833-07-19) (aged 75)Dunrobin Castle, SutherlandSpouseElizabeth Sutherland, 19th Countess of SutherlandChildren George Sutherland-Leveson-Gower, 2nd Duke of Sutherland Charlotte Fitzalan-Howard, Duchess of Norfolk Elizabeth Grosv...

Deutsche Schule La Paz (Spanish: Colegio Alemán Mariscal Braun) is a German international school in La Paz, Bolivia.[1] The school serves Kindergarten through grade 12 (Sekundarstufe/Secundaria 12). The school was founded on 10 May 1923.[2] See also Ethnic Germans in Bolivia References ^ Kontakt. Deutsche Schule La Paz. Retrieved on 23 March 2015. Avenida Alexander # 100 Achumani Casilla 605 – 4442 La Paz, Bolivien ^ Geschichte (Archive) / Historia (Archive). Deutsche Schul...

Ypres Tower oder Rye Castle Rye Castle, auch Ypres Tower (von französisch Ypres), von den Einheimischen The Wipers[1] genannt, ist eine Burg in Rye in der englischen Verwaltungseinheit East Sussex. Sie wurde 1249 auf Geheiß von König Heinrich III. als Bollwerk gegen die häufigen Überfälle der Franzosen gebaut. Damals war die englische Südküste unter permanenter Bedrohung durch die Franzosen, die mit England Krieg führten. Rye war eine der Cinque Ports und bekam so königliche...

У этого термина существуют и другие значения, см. Долгоруково. СелоДолгоруково Герб 52°18′32″ с. ш. 38°20′18″ в. д.HGЯO Страна Россия Субъект Федерации Липецкая область Муниципальный район Долгоруковский Сельское поселение Долгоруковское История и география Пе�...

Pakistani journalist and cricket administrator (born 1948) Najam Aziz Sethi نجم عزیز سیٹھیNajam Sethi at the launch of PSL in 2015Chairman of the Pakistan Cricket BoardIn office23 December 2022 – 22 June 2023Appointed byShehbaz SharifPresidentArif AlviPrime MinisterShehbaz SharifPreceded byRamiz RajaSucceeded byZaka AshrafIn office10 August 2017 – 20 August 2018Appointed byNawaz SharifPresidentMamnoon HussainPrime MinisterNawaz SharifImran KhanPreceded byShah...

Hospital de Niños Dr. Ricardo Gutiérrez LocalizaciónPaís ArgentinaLocalidad Gallo 1330 Buenos Aires ArgentinaCoordenadas 34°35′39″S 58°24′43″O / -34.594191944444, -58.41207Datos generalesFundación 30 de abril de 1875Sistema asistencia PúblicoEspecialidad PediatríaSitio web oficial[editar datos en Wikidata] El hospital de Niños Ricardo Gutiérrez es un hospital pediátrico creado el 30 de abril de 1875 cuya creación impulsó R...
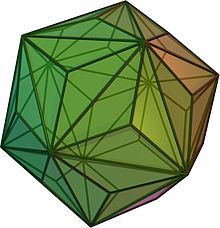
The triakis icosahedron, a polyhedron in which every edge has endpoints with total degree at least 13 In graph theory and polyhedral combinatorics, areas of mathematics, Kotzig's theorem is the statement that every polyhedral graph has an edge whose two endpoints have total degree at most 13. An extreme case is the triakis icosahedron, where no edge has smaller total degree. The result is named after Anton Kotzig, who published it in 1955 in the dual form that every convex polyhedron has two ...

Harvest festival in East India SohraiCelebration of Sohrai Khunta by Santal peopleTypeCultural, seasonalCelebrationslighting Diya, home decoration, performing rituals and feastDateKartik AmavasyaFrequencyannualRelated toBandna Sohrai is a harvest festival of the Indian states of Jharkhand, West Bengal, Chhattisgarh, Odisha, and Bihar. It also called cattle festival. It is celebrated after harvest and coincide with Govardhan Puja of Diwali festival.[1][2] It is celebrated ...

2013 computer animated film produced by Walt Disney Animation Studios FrozenTheatrical release posterDirected by Chris Buck Jennifer Lee Screenplay byJennifer LeeStory by Chris Buck Jennifer Lee Shane Morris Produced byPeter Del VechoStarring Kristen Bell Idina Menzel Jonathan Groff Josh Gad Santino Fontana CinematographyScott Beattie (layout)Mohit Kallianpur (lighting)Edited byJeff DraheimMusic by Christophe Beck (score) Robert Lopez (songs) Kristen Anderson-Lopez (songs) Productioncompanies...

Church in London Borough of Tower Hamlets, United KingdomTrinity Independent ChapelThe New Trinity Congregational Church 1951–presentLocationLondon Borough of Tower HamletsCountryUnited KingdomDenominationCharismatic Baptist, earlier Methodist and CongregationalistArchitectureArchitect(s)William Hosking and John Jay The Trinity Independent Chapel (also known as the Congregational or Methodist chapel) was an early Victorian church in Poplar. It was destroyed by a V-2 rocket hit during the Se...

Mumbo IslandSouth-Eastern shore of the island as seen from the southernmost peninsulaMumbo IslandGeographyLocationLake MalawiCoordinates13°59′21″S 34°45′20″E / 13.98921°S 34.75543°E / -13.98921; 34.75543Total islands1Area514 m2 (5,530 sq ft)AdministrationMalawiRegionCentral RegionDistrictSalima Mumbo Island is an island within Lake Malawi National Park, located in the Salima District of the Central Region, some 100 kilometers (62 miles) east ...

The Quintessential QuintupletsMusim 1Gambar visual kunciNegara asalJepangJumlah episode12RilisSaluran asliTBSTanggal tayang10 Januari (2019-01-10) –28 Maret 2019 (2019-3-28)Kronologi MusimSelanjutnya →Musim 2 Daftar episode The Quintessential Quintuplets Go-Tōbun no Hanayome (Jepang: 五等分の花嫁code: ja is deprecated , terj. har. Pengantin Kembar Lima), yang dirilis dalam bahasa Inggris dengan judul The Quintessential Quintuplets, adalah sebuah seri anime yang ...

American politician This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2021) (Learn how and when to remove this template message) Joel JonesBorn(1795-10-26)October 26, 1795Coventry, ConnecticutDiedFebruary 3, 1860(1860-02-03) (aged 64)Philadelphia, PennsylvaniaNationalityAmericanEducation Yale University Law School in Litchfield, Connecticut Occupation...




















![{\displaystyle [A,B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1993067bb075f2ebfa02e78959b7c5bed68e06f4)


![{\displaystyle \Delta _{\psi }A\,\Delta _{\psi }B\geqslant {\frac {1}{2}}\left|\left\langle \left[A,{B}\right]\right\rangle _{\psi }\right|,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7461fc2ea153b0cf97a258e9f5af97e9a5142d6c)






















