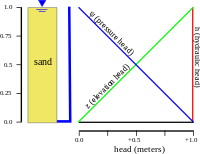
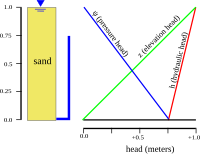
Hydraulic head
|
Read other articles:

Indian music director This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: T. G. Lingappa – news · newspapers · books · scholar · JSTOR (December 2010) (Learn how and when to remove this template message) T. G. LingappaBornThiruchirappalli Govindarajulu Lingappa(1927-08-22)22 August 1927Tiruchirappalli, Madras Pr...

Kentang ulirTempat asalKoreaBahan utamaKentang, minyak goreng Media: Kentang ulir Nama KoreaHangul회오리감자 Alih Aksarahoeori-gamjaMcCune–Reischauerhoeori-kamjaIPA[hwe̞.o.ɾi.ɡam.dʑa] Kentang ulir (Korea: 회오리 감자; hoeori gamja, bahasa Inggris: twist potatoes, tornado fries)[1][2] adalah sebuah makanan jalanan populer di Korea Selatan,[3] yang aslinya dikembangkan oleh Jeong Eun Suk dari Agricultural Hoeori Inc.[1][4]...

Gabriella Cilmi Gabriella Cilmi le 18 octobre 2008 au Royal Armouries Museum à Leeds au Royaume-Uni.Informations générales Nom de naissance Gabriella Lucia Cilmi Naissance 10 octobre 1991 (32 ans)Melbourne Nationalité Australienne Italienne Activité principale Chanteuse Genre musical Pop, funk rock, soul Années actives depuis 2005 Labels Warner MusicIsland Records modifier Gabriella Cilmi (/tʃilmi/) est une chanteuse australo-italienne, née le 10 octobre 1991 à Melbourne[1]. Ell...

1970s–1980s political movement in Taiwan You can help expand this article with text translated from the corresponding article in Chinese. (January 2016) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not t...

Spread of the German language, people and culture Germanisation, or Germanization, is the spread of the German language, people, and culture. It was a central idea of German conservative thought in the 19th and the 20th centuries, when conservatism and ethnic nationalism went hand in hand. In linguistics, Germanisation of non-German languages also occurs when they adopt many German words. Under the policies of states such as the Teutonic Order, Austria, the Kingdom of Prussia, and the German ...

Sugiono beralih ke halaman ini. Untuk orang lain dengan nama yang sama, lihat Sugiono (disambiguasi). Sugiyono MangunwiyotoInformasi pribadiLahir12 Agustus 1926Gedaren, Sumbergiri, Ponjong, Gunung KidulMeninggal1 Oktober 1965 (umur 39)Kentungan, YogyakartaMakamTMP Semaki, YogyakartaSuami/istriNy. SupriyatiAnak1. R. Erry Guthomo (l. 1954)2. R. Agung Pramuji (l. 1956)3. R. Haryo Guritno (l. 1958)4. R. Danny Nugroho (l. 1960)5. R. Budi Winoto (l. 1962)6. R. Ganis Priyono (l. 1963)7. Rr. Sugiarti...

Die Zisterzienserinnenabtei St. Marienthal in der Oberlausitz Zisterzienserinnen sind Nonnen, die dem Zisterzienserorden (OCist) angehören. Der weibliche und männliche Zweig bilden zusammen eine Ordensgemeinschaft. Inhaltsverzeichnis 1 Geschichte 2 Bestehende Nonnenklöster der Zisterzienser 2.1 Bestehende Nonnenklöster in Deutschland 2.2 Bestehende Nonnenklöster in Österreich 2.3 Bestehende Nonnenklöster in der Schweiz 3 Literatur 4 Weblinks 5 Einzelnachweise Geschichte Ein erstes...

Final Piala Dunia Antarklub FIFA 2013TurnamenPiala Dunia Antarklub FIFA 2013 Bayern München Raja Casablanca 2 0 Tanggal21 Desember 2013 (2013-12-21)StadionStade de Marrakech, MarrakeshPemain Terbaik Franck Ribéry (Bayern München)WasitSandro Ricci (Brasil)Penonton37.774CuacaMalam cerah13 °C (55 °F)Kelembapan 65%← 2012 2014 → Final Piala Dunia Antarklub FIFA 2013 adalah pertandingan babak final dari Piala Dunia Antarklub FIFA 2013, suatu turnamen sepak bola yang ...

American political organization This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Stonewall Young Democrats – news · newspapers · books · scholar · JSTOR (Ma...

Public school in Cary, North Carolina US Cary High SchoolAddress638 Walnut StCary, Wake, North Carolina 27511U.S.InformationFormer namesCary Senior High School Cary Public High School and Farm Life SchoolTypePublicMottoCognitio Vincit(Knowledge Conquers)Established1896 (127 years ago) (1896)School districtWake County Public School SystemNCES District ID3704720CEEB code340600NCES School ID370472001844PrincipalNolan BryantTeaching staff120Grades9–12Number of students2,071Stu...

This article is part of a series onPolitics of Japan Constitution and Laws Constitution of Japan (1947-present) Meiji Constitution (1890-1947) Laws The Monarchy The Emperor (List) Naruhito Crown Prince Fumihito Imperial House Chrysanthemum Throne Imperial Succession Imperial Household Agency Executive Government Prime Minister (List) Fumio Kishida (LDP) Cabinet (List) Second Kishida Cabinet (Second Reshuffle)(LDP-Komeito coalition) Ministries Administrative Agencies Legislature National Diet ...

Landak jawa Hystrix javanica Status konservasiRisiko rendahIUCN10752 TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoRodentiaFamiliHystricidaeGenusHystrixSpesiesHystrix javanica F.Cuvier, 1823 Sinonim taksonAcanthion sumbawae (en) Distribusi lbs Landak jawa (Hystrix javanica) adalah jenis hewan pengerat dari suku Hystricidae yang merupakan hewan endemik dari Indonesia. Meskipun tidak terdaftar sebagai hewan yang terancam eksistensinya di alam oleh IUCN, landak jawa diburu orang karena ...

2015 studio album by ThighpaulsandraThe Golden CommunionStudio album by ThighpaulsandraReleased4 September 2015RecordedAerial Studios; Golliwog Farm, Wales; North Tower; Rockfield Studios, 2005-2015GenreIndustrial, experimental music, psychedelic rock, progressive rockLength116:54LabelEditions MegoEMEGO 207ProducerThighpaulsandraThighpaulsandra chronology The Clisto E.P.(2007) The Golden Communion(2015) The Golden Communion is the sixth album by Thighpaulsandra, released on 4 Septembe...

American actor For other people named Francis McDonald, see Francis McDonald (disambiguation). Francis McDonaldMcDonald and Shirley Mason inThe Final Close-Up (1919)Born(1891-08-22)August 22, 1891Bowling Green, Kentucky, U.S.DiedSeptember 18, 1968(1968-09-18) (aged 77)Hollywood, California, U.S.Resting placeValhalla Memorial Park Cemetery in North Hollywood, CaliforniaOccupationActorYears active1913–1965Spouses Mae Busch (m. 1915; div. ...

Political party in Egypt Egyptian Patriotic Movement الحركة الوطنية المصريةLeaderIbrahim Darwish[1]FounderAhmed Shafiq[1] and Mohamed Abu Hamed[2]Founded2 December 2012[1]HeadquartersCairoIdeologySecularism[3]ReformismNational affiliationEgyptian Front[4]House of Representatives4 / 568Websitehttp://elharakaelwatanyaelmasrya.com/Politics of EgyptPolitical partiesElections The Egyptian Patriotic Movement, or Egyptian National M...

American rapper This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (April 2017) (Learn how and when to remove this tem...

The West Kowloon Bamboo Theatre, emblazoned with flower plaques, in 2012 West Kowloon Bamboo Theatre is one of the flagship programmes of the West Kowloon Cultural District Authority (WKCDA). The West Kowloon Bamboo Theatre has been held since 2012 by the WKCDA which aims to promote Cantonese opera and the West Kowloon Cultural District (WKCD). Due to its popularity, the WKCDA continues to organise the West Kowloon Bamboo Theatre annually after 2012. Starting from 2013, apart from Cantonese o...

Dieser Artikel beschreibt den Begriff der wirtschaftlichen Kosten. Für weitere Bedeutungen siehe Kosten (Begriffsklärung). Gewinnschwelle (Break-even-Point) aus Erlös und Kosten Kosten (englisch cost) sind die monetären Belastungen, die einer Wirtschaftseinheit gemäß einer geeigneten Kalkulation durch die Nutzung von Produktionsfaktoren entstehen. Der Kostenbegriff wird sowohl in der Betriebswirtschaftslehre als auch in der Volkswirtschaftslehre verwendet und hat dort – wegen des unt...

National Wildlife Refuge in North Carolina, United States Cedar Island National Wildlife RefugeIUCN category IV (habitat/species management area)Map of the United StatesShow map of the United StatesCedar Island National Wildlife Refuge (North Carolina)Show map of North CarolinaLocationCarteret County, North Carolina, United StatesNearest cityBeaufort, North CarolinaCoordinates34°57′N 76°20′W / 34.950°N 76.333°W / 34.950; -76.333Area14,480 acres (58.6 ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ranganathaswamy Temple, Bangalore – news · newspapers · books · scholar · JSTOR (February 2022) (Learn how and when to remove this template message) Hindu temple in Karnataka, India Ranganathaswamy TempleReligionAffiliationHinduismDistrictBangaloreDeityLord Ra...