Free module
|
Read other articles:

Salah satu tokoh dalam Konsili Efesus Latrosinium sering disebut sebagai Konsili Penyamun.[1] Paus Leo I (440-461) menyebut Konsili Efesus sebagai Konsili Penyamun karena Konsili itu dilakukan dengan menggunakan kekerasan dan tidak menggunakan prosedur yang jelas, sehingga hak Paus untuk mengadili dirampas.[2] Nama ini diberikan kepada Konsili yang diadakan di Efesus pada tahun 449.[1] Kaisar Theodosius II adalah orang yang memerintahkan diadakannya Konsili ini.[1&...

PostasoftwareLogoSchermata dell'applicazione su Windows 10Schermata dell'applicazione su Windows 10 GenereClient di posta SviluppatoreMicrosoft Corporation Sistema operativoMicrosoft Windows LicenzaProprietario(licenza non libera) Sito webwww.microsoft.com/ Modifica dati su Wikidata · Manuale Posta (già Windows Mail) è un client di posta elettronica e newsgroup creato da Microsoft ed incluso nel sistema operativo Windows Vista, Windows 8, Windows 8.1 e Windows 10.[1][2]...

Swedia baru tahun 1650. Swedia Baru, atau Nya Sverige, adalah pemukiman Swedia kecil di sepanjang sungai Delaware di pantai Atlantik Amerika Utara. Swedia Baru berpusat di Benteng Christina, kini di Wilmington, Delaware, dan termasuk negara bagian Delaware, New Jersey, dan Pennsylvania di Amerika Serikat sekarang ini. Pemukiman ini didirikan pada tanggal 29 Maret 1638, dan tergabung kepada Belanda Baru pada tanggal 15 September 1655. Bersama dengan bangsa Swedia, sejumlah besar penetap adalah...

Berikut daftar Kepala Daerah dan Wakil Kepala Daerah di 9 kabupaten/kota di Bali adalah: Kabupaten/Kota Foto Bupati/Wali Kota Bupati/Wali Kota Foto Wakil Bupati/Wali Kota Wakil Bupati/Wali Kota Mulai Menjabat Selesai Menjabat(Direncanakan) Ref KabupatenBadungDaftar Bupati/Wakil Bupati I Nyoman Giri Prasta I Ketut Suiasa 26 Februari 2021 26 Februari 2024 [1] KabupatenBangliDaftar Bupati/Wakil Bupati Sang Nyoman Sedana Arta I Wayan Diar 26 Februari 2021 26 Februari 2024 [1] Kabu...

Носенко Іван СидоровичНародився 19 квітня 1902(1902-04-19)Берлевець, Q4062175?, Дубровський район, РосіяПомер 2 серпня 1956(1956-08-02) (54 роки)Москва, СРСРПоховання Некрополь біля Кремлівської стіниКраїна СРСРДіяльність політикAlma mater Національний університет кораблебудування імені а�...
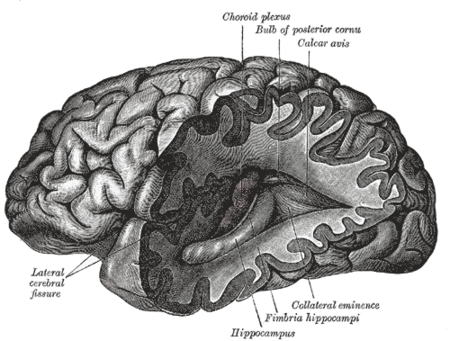
اضطراب النمو العصبي تعديل مصدري - تعديل اضطرابات النمو العصبي هو ضعف النمو وتطور الدماغ أو الجهاز العصبي المركزي.[1][2] يشير هذا المصطلح باختصار إلى اضطراب في وظيفة الدماغ التي تؤثر على العاطفة، القدرة على التعلم، وضبط النفس والذاكرة والتي تكشف عن نمو الفرد. الأن...

Petrus KasihiwBupati Teluk Bintuni ke-3PetahanaMulai menjabat 18 Juni 2021PresidenJoko WidodoGubernurDominggus MandacanWakilMatret KokopMasa jabatan17 Juni 2016 – 17 Juni 2021PresidenJoko WidodoGubernurAbraham Octavianus AtururiEko Subowo (Pj.)Dominggus MandacanWakilMatret KokopPendahuluAlfons ManibuiIshak Laurens Hallatu (Pj.) Informasi pribadiLahir8 November 1964 (umur 59)Bintuni, Papua BaratKebangsaanIndonesiaPartai politik NasDemSunting kotak info �...
Cet article dresse la liste des aéroports les plus fréquentés sur l'île. Évolution en graphique de Keflavik Pour des raisons techniques, il est temporairement impossible d'afficher le graphique qui aurait dû être présenté ici. Voir la requête brute et les sources sur Wikidata. Évolution en graphique en dehors de Keflavík Pour des raisons techniques, il est temporairement impossible d'afficher le graphique qui aurait dû être présenté ici. Voir la requête brute et les sources s...

Caste in India This article is about the Bairagi caste. For Hindustani classical raga, see Bairagi (raga). Not to be confused with the Celibate Ascetics (Vairagi). BairagiSwami • Vaishnav • MahantA Portrait of Bairagi Mahant(Tilak of Ramanandi Sampradaya on his body)ClassificationRamanandi Sampradaya • Nimbarka Sampradaya • Vishnuswami Sampradaya • Madhvacharya Sampradaya[1]Kuladevta (male)Rama • Krishna • (Avatars of Vishnu) • HanumanKuladevi (female)Sita • Radha•...

Lebanese and British barrister (born 1978) Amal ClooneyClooney in 2014BornAmal Alamuddin (1978-02-03) 3 February 1978 (age 45)Beirut, LebanonCitizenshipLebanonUnited KingdomEducationSt Hugh's College, Oxford (BA)New York University (LLM)OccupationBarristerYears active2000–presentSpouse George Clooney (m. 2014)Children2 Amal Clooney (née Alamuddin; Arabic: أمل كلوني; born 3 February 1978)[1] is a Lebanese and British barrister.&#...

Fictional character from the television series Holby City Fictional character Nicky McKendrickHolby City characterBelinda Owusu as Nicky McKendrickFirst appearanceWe Need to Talk About Fredrik12 December 2017Last appearanceEpisode 110229 March 2022Portrayed byBelinda OwusuIn-universe informationOccupation CT3 doctor (prev. F1 doctor, F2 doctor, CT1 doctor) FamilyTracey McKendrick (mother)Significant otherCameron DunnLouis McGerry Nicky McKendrick is a fictional character from the BBC medical ...

Blade ManPoster promosi untuk Blade ManGenreRomansa Fantasi Drama KomediDitulis olehKim Kyu-wanSutradaraKim Yong-soo Kim Jong-yeonPemeranLee Dong-wook Shin Se-kyungNegara asalKorea SelatanBahasa asliKoreaJmlh. episode18ProduksiProduser eksekutifBae Kyung-sooProduserIm Se-joonLokasi produksiKoreaRumah produksiiHQ Gazi ContentsRilis asliRilis10 September (2014-09-10) –13 November 2014 (2014-11-13) Blade Man (Hangul: 아이언맨; RR: Aieonmaen; lit. Iron M...

A neutralidade deste artigo foi questionada. Discussão relevante pode ser encontrada na página de discussão. Governo Anastasia de Minas Gerais Gestão Antônio Anastasia no governo de Minas Gerais Gestão Antonio Anastasia no governo de Minas GeraisAnastasia em 2015. Governador de MinasGerais Período 31 de março de 2010a 4 de abril de 2014 Vice-governador Nenhum (2010–2011) Alberto Pinto Coelho Júnior (2011–2014) Antecessor(a) Aécio Neves Sucessor(a) Alberto Pinto Coelho Júnior Pa...

У этого термина существуют и другие значения, см. Алгебра (значения). Трёхмерный правильный коноид, описанный тригонометрическими уравнениями x = v × cos ( u ) {\displaystyle x=v\times \cos(u)} , y = v × sin ( u ) {\displaystyle y=v\times \sin(u)} , z = 2 × sin ( u ) {\displaystyle z=2\times \sin(u)} А́лгебра (от ар...

See also: List of songs written by Natasha Bedingfield Natasha Bedingfield discographyStudio albums4Video albums1Music videos24EPs1Singles20 The English singer Natasha Bedingfield has released 4 studio albums, 20 singles, 24 music videos, and 1 video album. Bedingfield's debut album, Unwritten, was released in the United Kingdom in September 2004. It produced four singles: Single, These Words, which peaked at number one on the UK Singles Chart, Unwritten and I Bruise Easily. The album reached...

New Zealand demographer (1936–2022) Ian PoolCNZM FRSNZPool in 2013BornDavid Ian Pool(1936-11-22)22 November 1936Auckland, New ZealandDied28 April 2022(2022-04-28) (aged 85)Hamilton, New ZealandAlma materAustralian National UniversitySpouseJanet SceatsChildren2Scientific careerFieldsDemographyInstitutionsUniversity of WaikatoThesisThe Maori population of New Zealand (1964)Doctoral advisorW. D. Borrie David Ian Pool CNZM FRSNZ (22 November 1936 – 28 April 2022) was a ...

Former province of Japan Dewa Province出羽国Province of Japan712–1869Map of Japanese provinces (1868) with Dewa Province highlightedCapitalHiraka DistrictHistory • Established 712• Disestablished 1869 Preceded by Succeeded by Echigo Province Uzen Province Ugo Province Today part ofAkita PrefectureYamagata Prefecture Dewa Province (出羽国, Dewa no kuni) was a province of Japan comprising modern-day Yamagata Prefecture and Akita Prefecture,[1] except for the c...

World Series 1992 Competizione Major League Baseball 1992 Sport Baseball Edizione 89ª Organizzatore Major League Baseball Date dal 17 ottobreal 24 ottobre Sito web https://www.worldseries.com/ Risultati Vincitore Toronto Blue Jays(1º titolo) Finalista Atlanta Braves Statistiche Miglior giocatore Pat Borders Cronologia della competizione 1991 1993 Manuale Le World Series 1992 sono state la 89ª edizione della serie di finale della Major League Baseball al meglio del...

السيف الياباني (باليابانية: 日本刀، هيبورن: nihontō) هو واحد من الأسلحة التقليدية في اليابان.[1][2][3] هناك عدة أنواع من السيوف اليابانية، وفقا للحجم، مجال الاستخدام، طريقة التصنيع. التصنيف التصنيف حسب الفترة ينقسم إنتاج السيوف في اليابان إلى فترات زمنية محددة:[4] �...

只見川 只見川と蒲生岳。JR会津塩沢駅(寄岩橋)付近より水系 一級水系 阿賀野川種別 一級河川延長 145.2 km平均流量 -- m³/s流域面積 2,792.0 km²水源 尾瀬沼(福島県・群馬県)水源の標高 -- m河口・合流先 阿賀川(喜多方市)流域 日本群馬県・新潟県・福島県テンプレートを表示 第三只見川橋梁を渡るC11形蒸気機関車(1973年9月) 会津蒲生岳より見る只見川と寄岩�...










![{\displaystyle R[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afeccd52deabb878398a8485755c3ceea80caf9a)
![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f)
![{\displaystyle B=A[t]/(f)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/768151c0a8d11b44136db1811bee3ddd9ac55df5)






































