Four-velocity
|
Read other articles:
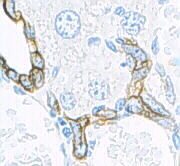
Microscopisch beeld van met een kleurstof bewerkt keratine Keratine is een eiwit dat als een structuurelement voorkomt bij dieren en is een klassiek voorbeeld van een vezeleiwit. Keratine is een taai, onoplosbaar eiwit dat voorkomt in onder andere de epidermis (buitenlaag) van de huid bij mens en vele dieren. De buitenste cellaag bevat keratine waardoor de huid taai en waterafstotend is. Bij eeltvorming op bijvoorbeeld handen en voeten neemt het aantal cellen met keratine sterk toe. Keratine ...

Dieser Artikel behandelt den Stadtteil und Stadtbezirk von Braunschweig. Zum ähnlich oder gleichnamigen Adelsgeschlecht siehe Broizem. Broitzem Stadt Braunschweig Wappen von Broitzem Koordinaten: 52° 14′ N, 10° 29′ O52.23444444444410.48083333333383Koordinaten: 52° 14′ 4″ N, 10° 28′ 51″ O Höhe: 83 m Einwohner: 5790 (31. Dez. 2020)[1] Eingemeindung: 1. März 1974 Postleitzahl: 38122 Vorwahl: 0531 Kar...

For the Opening Day starting pitchers prior to 1968, see List of Philadelphia and Kansas City Athletics Opening Day starting pitchers. The Oakland Athletics are a Major League Baseball (MLB) team based in Oakland, California. They play in the American League West division. The club was founded in Philadelphia in 1901, moved to Kansas City, Missouri in 1955 and relocated to Oakland in 1968.[1] The first game of the new baseball season for a team is played on Opening Day, and being name...

Адам Рапацький (24.12.1909, Львів -10.10.1970, Варшава) — польський політик, економіст і дипломат. Богдан Рапацький - український спортсмен, Універсальний кулачний бій Ю. А. Кострова. Рапацький — термін, який має кілька значень. Ця сторінка значень містить посилання на статті про ко�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أغسطس 2021) لمعانٍ أخرى، طالع الكوم الأخضر (توضيح). الكوم الأخضر - قرية مصرية - جانب من قرية الكوم الأخضر تقسيم إداري البلد مصر المحافظة المنوفية ال�...

British thriller series This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (August 2023) (Learn how and when to remove this template message) This article needs additional citations for verification. P...

The Annie Larsen affair was a gun-running plot in the United States during World War I.[1] The plot, involving India's Ghadar Party, the Irish Republican Brotherhood and the German Foreign office, was a part of the larger so-called Hindu–German Conspiracy,[2] and it was the prime offence cited in the 1917 Hindu–German Conspiracy Trial, described at the time as the longest and most expensive trial in American legal history.[3] Background Main article: Hindu–German...

Village in Ganja, AzerbaijanKrasnoye SeloVillageKrasnoye SeloCoordinates: 40°38′36″N 46°23′35″E / 40.64333°N 46.39306°E / 40.64333; 46.39306Country AzerbaijanCityGanjaTime zoneUTC+4 (AZT) • Summer (DST)UTC+5 (AZT) Krasnoye Selo is a village in Ganja, Azerbaijan. It is suspected that this village has undergone a name change or no longer exists, as no Azerbaijani website mentions it under this name. References Krasnoye Selo, Azerbaijan at GEO...

جزء من سلسلة مقالات سياسة البحرينالبحرين الدستور الدستور حقوق الإنسان حقوق المرأة السياسية الملكية الملك حمد بن عيسى بن سلمان آل خليفة الحكومة رئيس الوزراء خليفة بن سلمان آل خليفة وزارة الخارجية وزارة الداخلية وزارة العدل والشؤون الإسلامية والأوقاف وزارة المالية والاقت...

1957 film by Herman Hoffman This article is about the 1957 film. For the 2014 film, see The Invisible Boy (2014 film). For other uses, see Invisible Boy. The Invisible BoyFilm poster by Reynold BrownDirected byHerman HoffmanWritten byEdmund Cooper (story)Cyril HumeProduced byNicholas NayfackStarringRichard EyerPhilip AbbottDiane BrewsterHarold J. StoneCinematographyHarold E. WellmanEdited byJohn FaureMusic byLes BaxterDistributed byMetro-Goldwyn MayerRelease date October 1957 (1957-...

Szwajcaria Ten artykuł jest częścią serii:Ustrój i politykaSzwajcarii Ustrój polityczny Ustrój polityczny Szwajcarii Konstytucja Konstytucja Szwajcarii Władza ustawodawcza Zgromadzenie Federalne Rada Narodu Rada Kantonów Władza wykonawcza Prezydent Rada Związkowa Kanclerz federalny Szwajcarii Władza sądownicza Wymiar sprawiedliwości Federalny Sąd Najwyższy Federalny Trybunał Karny Federalny Sąd Administracyjny Prokurator Generalny Kontrola państwowa Kontrola państwowa Fina...

2016 mobile strategy video game 2016 video gameGirls' FrontlineDeveloper(s)MICA TeamPublisher(s)CHN: Dark WinterTWN: Longcheng TianxiaKOR: X.D. GlobalEN: Darkwinter SoftwareJPN: Sunborn JapanProducer(s)Yuzhong (羽中)EngineUnityReleaseCHN: 20 May 2016TWN: 18 January 2017HKG: 30 June 2017KOR: 30 June 2017EN: 8 May 2018JPN: 1 August 2018Genre(s)Strategy role-playing gameMode(s)Single-player Girls' Frontlineドールズフロントライン(Dōruzu Furontorain) MangaGirls' Frontline: The Song o...

1953 film by Seymour Friedman Flame of CalcuttaTheatrical release posterDirected bySeymour FriedmanWritten bySol ShorRobert E. KentProduced bySam KatzmanStarringDenise DarcelPatric KnowlesPaul CavanaghLeonard PennNarrated byFred F. SearsCinematographyRay CoryHenry FreulichEdited byJerome ThomsMusic byClifford VaughanMischa BakaleinikoffProductioncompanyEsskay PicturesDistributed byColumbia PicturesRelease dateJuly 20, 1953Running time69 minutesCountryUnited StatesLanguageEnglish Flame of Calc...

2018 video gameBasingstokeDeveloper(s)Puppy GamesPublisher(s)Puppy GamesEngineUnityPlatform(s)Microsoft Windows, Linux, macOSRelease27 April 2018Genre(s)Roguelike, stealthMode(s)Single-player Basingstoke is a roguelike and stealth video game developed and published by Puppy Games. It was released on Microsoft Windows, Linux, and macOS on 27 April 2018.[1][2][3] Gameplay The player must escape an invasion of deadly aliens on foot, using their wits and cunning.[...

Serbian poet Vasko PopaВаско ПопаPortrait of Popa by photographer Stevan Kragujević, 1990Born(1922-06-29)29 June 1922Grebenac, Yugoslavia(now Serbia)Died5 June 1991(1991-06-05) (aged 68)Belgrade, SR Serbia, YugoslaviaOccupation(s)poet, writer, editor, translator Vasile Vasko Popa (Serbian Cyrillic: Васко Попа; 29 June 1922 – 5 January 1991) was a Serbian poet. Biography Васко Попа Popa was born in the village of Grebenac (Romanian: Grebenaț), Yugoslavia (pr...

Otot jantungOtot jantungOtot jantung pada anjing, perbesaran 400XRincianPengidentifikasiBahasa Latintextus muscularis striatus cardiacusMeSHD009206TA98A12.1.06.001TA23950FMA9462Daftar istilah anatomi[sunting di Wikidata] Gambar 3D yang menunjukkan miokardium (myocardium), yang disusun oleh otot jantung, sebagai salah satu lapisan dinding jantung. Otot jantung atau adalah otot tidak sadar yang membentuk miokardium, yaitu dinding jantung di antara perikardium dan endokardium. Otot jantung a...

Charron (Charron, Girardot et Voigt, CGV) Основание 1901 Упразднена 1930 Расположение Франция Отрасль Автомобилестроение Продукция Легковые автомобили, грузовые автомобили, бронеавтомобили Медиафайлы на Викискладе Шаррон, Жирардо э Вуа (фр. Charron, Girardot et Voigt; с 1907 года — Charron) — ф�...

BangkokกรุงเทพมหานครKrung Thep Mahanakhon Capital de Tailandia BanderaEscudo BangkokLocalización de Bangkok en TailandiaCoordenadas 13°45′00″N 100°31′00″E / 13.75, 100.51666666667Idioma oficial TailandésEntidad Capital de Tailandia • País Tailandia • Región Tailandia Central • Provincia Área administrativa especialAlcalde Chadchart SittipuntEventos históricos • Fundación 21 de abril de 1782Supe...

Динамика роста интуристов в Японии с 2003 по 2017 Туризм в Японии — отрасль экономики Японии. В 2019-ом году Япония привлекла 31,88 млн. международных туристов[1]. В Японии 21 объект Всемирного наследия, включая замок Химэдзи, исторические памятники Киото и Нары. В докладе о кон�...

18th century coffee house in Covent Garden, London This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (September 2016) (Learn how and when to remove this template message) Detail from Hogarth's Four Times of the Day, showing a fight breaking out in Tom King's coffee house Tom King's Coffee House (later known as Moll King's Co...
![{\displaystyle {\vec {x}}(t)={\begin{bmatrix}x^{1}(t)\\[0.7ex]x^{2}(t)\\[0.7ex]x^{3}(t)\end{bmatrix}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61179c0e926675effb8b5e70e63d297ecf2cba92)


































