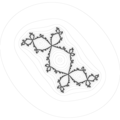
Douady rabbit
|
Read other articles:

This article is about recent and past political developments in Senegal. For the Senegal government, see Government of Senegal.Political system of Senegal Politics of Senegal Constitution Human rights Government President Macky Sall Prime Minister Amadou Ba Cabinet of Senegal Parliament National Assembly Speaker: Moustapha Niasse Judiciary Court of Cassation Administrative divisions Regions Departments Arrondissements Communes Rural communities Elections Recent elections Presidential: 2012201...

DC Comics character Comics character Granny GoodnessGranny GoodnessArt by Jack KirbyPublication informationPublisherDC ComicsFirst appearanceMister Miracle #2 (May 1971)Created byJack KirbyIn-story informationAlter egoGoodnessSpeciesNew GodPlace of originApokolipsTeam affiliationsFemale FuriesDarkseid's EliteNotable aliasesAthenaAbilities Superhuman strength, speed, stamina, and durability Immortality Expert strategist, tactician, and field commander Skilled warrior Wields mega-rod and advanc...

Gimnasia y Esgrima de Pergamino Datos generalesNombre Club de Gimnasia y EsgrimaApodo(s) Lobo - Mens SanaFundación 1 de enero de 1921 (102 años)Presidente Mariano BallestraseInstalacionesEstadio Atilio Saint Julien/Socios FundadoresUbicación Pergamino, Bs AsRegional Liga de Pergamino Actualidad Gimnasia y Esgrima de Pergamino (Facebook)[editar datos en Wikidata] El Club de Gimnasia y Esgrima es una institución dedicada al deporte en la localidad bonaerense de Pergamin...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2019) زولت فيهير معلومات شخصية الميلاد 15 يونيو 1975 (48 سنة) سغليد الطول 1.90 م (6 قدم 3 بوصة) مركز اللعب مدافع الجنسية المجر معلومات النادي النادي الحال�...

Pour un article plus général, voir Championnats du monde d'athlétisme. 100 m haies aux championnats du monde d'athlétisme Finale du 100 m haies lors des championnats du monde 2019.Généralités Sport Athlétisme100 m haies Organisateur(s) World Athletics Éditions 18e en 2022 Catégorie Championnats du monde Palmarès Tenant du titre Danielle Williams (2023) Plus titré(s) Gail Devers (3) Records Tobi Amusan (12 s 12, 2022) modifier Le 100 mètres haies fait partie des épreuves ins...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Pakandei atau pakaddei adalah upacara adat menyambut besan yang dilaksanakan oleh Suku Mentawai, terutama di Kecamatan Siberut Utara. Upacara adat ini merupakan rangkaian upacara perkawinan berupa pesta makan daging babi bersama. Upacara pakandei dapa...

Stasiun Wanaraja C31 Stasiun Wanaraja yang sudah selesai direnovasi, 2020LokasiWanasari, Wanaraja, Garut, Jawa BaratIndonesiaKetinggian+692 mOperatorKAI CommuterLetak dari pangkalkm 9+100 lintas Cibatu-Cikajang[1]Jumlah peronDua peron sisi yang tinggiJumlah jalur2 (jalur 1: sepur lurus)KonstruksiAkses difabelAdaInformasi lainKode stasiunWNR1824[2]KlasifikasiIII/kecil[butuh rujukan]SejarahDibuka14 Agustus 1889; 134 tahun lalu (1889-08-14)Ditutup1983; 40 tahun lalu&...

لمعانٍ أخرى، طالع محمد جمال (توضيح). محمد جمال معلومات شخصية الاسم الكامل محمد جمال باظفاري الميلاد 11 مايو 1994 (العمر 29 سنة)أبوظبي، الإمارات الطول 1.73 م (5 قدم 8 بوصة) مركز اللعب لاعب وسط الجنسية الإمارات العربية المتحدة معلومات النادي النادي الحالي الجزيرة الر

Друга лігаСезон 2015—2016Підвищилися «Колос»«Верес»«Інгулець»«Буковина»«Скала»«Арсенал-Київ»Вибули «Барса»Зіграно матчів 182Забито голів 487 (2.68 за гру)Найкращий бомбардир Олександр Бондаренко («Колос») − 20Найбільша перемога вдома 8:0 («Кремінь» — «Арсенал-Київщина»)

Kurt KüttnerKurt KüttnerNickname(s)Kiwe (Yiddish)Died1964Allegiance Nazi GermanyService/branch SchutzstaffelRank SS-Oberscharführer (Staff Sergeant)Commands heldLower camp of Treblinka Kurt Küttner (1907 – 1964) was an SS-Oberscharführer (Staff Sergeant) who served at Treblinka extermination camp, arrested and charged with war crimes at the Treblinka trials twenty years after the war ended. Career Before World War II, Kurt (Fritz)[1] Küttner worked for many years as a war...

Ingrid Hack (2017) Ingrid Hack (* 28. Juli 1964 in Köln) ist eine deutsche Politikerin (SPD). Sie war Abgeordnete des Landtags von Nordrhein-Westfalen. Leben & Politik Hack machte 1983 ihr Abitur in Dormagen und studierte Germanistik, Geschichte und Politologie an der Universität zu Köln. 1992 beendete sie ihr Studium mit dem Magisterabschluss. Ab 1986 arbeitete sie als Verlagsangestellte und nach einer berufsbegleitenden Ausbildung zur Marketing-Fachwirtin im Bereich Öffentlichkeitsa...

For the data downloading process, see sideloading. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Transloading – news · newspapers · books · scholar · JSTOR (May 2009) (Learn how and when to remove this template message) A transloading facility in Texas, between rail and road transport Transloading, also kn...

Núi SugarloafCon đường dẫn lên đỉnh núi SugarloafĐộ cao312 ft (95 m)[1]Phần lồi245 ft (75 m)[1]Vị tríNúi SugarloafVị trí tại FloridaVị tríQuậnLake, Florida,Hoa KỳDãy núiLake Wales RidgeTọa độ28°38′58″B 81°43′59″T / 28,6494413°B 81,7331317°T / 28.6494413; -81.7331317[2]Địa chấtTuổi đá~2.000.000 nămLeo núiHành trình dễ nhấtĐi bộ, đường lộ Núi Sugar...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Evil Ladytron song – news · newspapers · books · scholar · JSTOR (August 2016) (Learn how and when to remove this template message) 2003 single by LadytronEvilSingle by Ladytronfrom the album Light & Magic Released30 June 2003Recorded2003Genre Electrop...

Ini adalah nama Minahasa, marganya adalah Gerung. Rocky GerungLahir20 Januari 1959 (umur 64)Manado, Sulawesi Utara, IndonesiaKebangsaanIndonesiaAlmamaterUniversitas IndonesiaPekerjaanAkademikus, konten kreatorDikenal atasFilsafat kontemporer dan aktivis masyarakatInformasi YouTubeKanal Rocky Gerung Official Tahun aktif2019–sekarangGenreBeritaPelanggan1,84 juta[1](Hingga 2 Desember 2023[update])Total tayang322,757,350[1](Hingga 2 Desember...

Television channel Times Now NavbharatCountryIndiaBroadcast areaWorldwideHeadquartersNoida, Uttar Pradesh, IndiaProgrammingLanguage(s)HindiPicture format4:3 (576i, SDTV) 16:9 (1080i, HDTV)OwnershipOwnerThe Times GroupSister channelsTimes NowZoomET NowMovies NowRomedy NowMN+MNXMirror NowHistoryLaunched1 August 2021; 2 years ago (2021-08-01)LinksWebsitewww.timesnowhindi.comAvailabilityStreaming mediaLive StreamWatch Live Times Now Navbharat is a Hindi News TV Channel.[1 ...

American fictional character For the hotel chain founder, see Intown Suites. Soap opera character David VickersOne Life to Live characterPortrayed byTuc WatkinsDuration 1994–1996 2001–2013 First appearanceMay 6, 1994 (May 6, 1994)Last appearanceAugust 2013ClassificationFinal; regularCreated byMichael Malone and Josh GriffithIntroduced byLinda Gottlieb (1994)Gary Tomlin (2001)Jennifer Pepperman (2013)CrossoverappearancesAll My ChildrenIn-universe informationOt...

2008 compilation album by Various ArtistsWOW Gospel 2008Compilation album by Various ArtistsReleasedFebruary 12, 2008GenreCCM, GospelLabelVerity RecordsVarious Artists chronology WOW Gospel 2007(2007) WOW Gospel 2008(2008) WOW Gospel 2009(2009) Professional ratingsReview scoresSourceRatingAllmusic[1]The Phantom Tollbooth[2] WOW Gospel 2008 is a gospel music compilation album in the WOW series. Released on February 12, 2008, it comprises thirty-three songs on a double C...

Lena Hentschel Medallista olímpica Datos personalesNacimiento Berlín, Alemania17 de junio de 2001 (22 años)Carrera deportivaRepresentante de Alemania AlemaniaDeporte Salto Medallero Salto femenino Evento O P B Juegos Olímpicos 0 0 1 Campeonato Mundial 0 0 1 Juegos Europeos 0 1 0 Campeonato Europeo 2 2 0 [editar datos en Wikidata] Lena Hentschel (Berlín, 17 de junio de 2001) es una depo...

I Prevail Основная информация Жанр пост-хардкорметалкорню-металкор Годы 2014 — настоящее время Страна США Место создания СаутфилдМичиган Язык английский Лейбл Fearless Records Состав Брайан Буркейзер Эрик Ванлерберг Стив Меноян Дилан Боумен Бывшиеучастники Джордан Бергер Ли Р�...