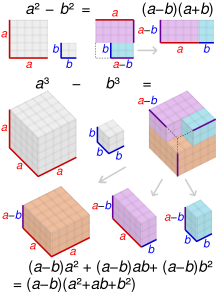
Difference of two squares
|
Read other articles:

Cờ Thống đốc các khu định cư Eo biển (1867–1946) Thống đốc Các khu định cư Eo biển cai trị các khu định cư eo biển. Những người đàn ông giữ vị trí này cai quản Định cư Eo biển từ năm 1826 đến năm 1946, thay mặt cho Công ty Đông Ấn Anh (cho đến năm 1858), Văn phòng Ấn Độ (cho đến năm 1867) và Văn phòng Thuộc địa (cho đến năm 1946).[1] Khi không có thống đốc, thư ký trưởng nga...
4625 ЩедрінВідкриттяВідкривач Карачкіна Людмила ГеоргіївнаМісце відкриття КрАОДата відкриття 20 жовтня 1982ПозначенняНазвана на честь Щедрін Родіон КостянтиновичТимчасові позначення 1982 UG6 1975 BO 1982 XR4 1986 RC17Категорія малої планети Астероїд головного поясуОрбітальні характ�...

Ла Крещенте порт. La Creciente Континент Південна АмерикаКраїна КолумбіяРегіон Lower Magdalena ProvincedВідкрито листопад 2006[1]Розробка 28 грудня 2007[1]Дотично petroleum industry in Colombiad Література Oil & Gas Journal Корисні копалини Південної Америки Геологія Південної Америки Гірнича промис

American aerospace engineer and executive (1887–1956) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Frederick Rentschler – news · newspapers · books · scholar · JSTOR (August 2010) (Learn how and when to remove this template message) Frederick RentschlerRentschler in 1929Born(1887-11-08)November 8, 1887H...

شجيرة حناء وقمرمعلومات عامةالمؤلف أحمد التوفيقاللغة عربيةالبلد المغربالنوع الأدبي روايةالناشر القبة الزرقاء للنشرتاريخ الإصدار 1998التقديمعدد الأجزاء واحدتعديل - تعديل مصدري - تعديل ويكي بيانات شجيرة، حناء وقمر هي رواية للكاتب والمؤرخ المغربي أحمد التوفيق.[1][2&#...

Lighthouse in South Carolina, US LighthouseMorris Island Light Morris Island LighthouseLocationMorris Island, South Carolina (Charleston harbor entrance)Coordinates32°41′43″N 79°53′1″W / 32.69528°N 79.88361°W / 32.69528; -79.88361TowerConstructed1767 FoundationTimber piling, concrete baseConstructionDressed stoneAutomated1938Height161 feet (49 m)ShapeConicalHeritageNational Register of Historic Places listed place LightFirst lit1876Deacti...

6th episode of the 3rd season of Game of Thrones The ClimbGame of Thrones episodeEpisode no.Season 3Episode 6Directed byAlik SakharovWritten byDavid BenioffD. B. WeissFeatured musicRamin DjawadiCinematography byDavid KatznelsonEditing byOral Norrie OtteyOriginal air dateMay 5, 2013 (2013-05-05)Running time53 minutesGuest appearances Diana Rigg as Olenna Tyrell Gwendoline Christie as Brienne of Tarth Michael McElhatton as Roose Bolton Paul Kaye as Thoros of Myr Richard Dorm...

Motor vehicle Volkswagen ConstellationOverviewManufacturerVolkswagen Truck & BusProduction2005–presentAssemblyResende, Brazil[1]Quezon City, Philippines (MACC)Body and chassisClassCommercial vehicle - truckBody styleTractor unit, Chassis cab, Flatbed - all cab-over-engine Volkswagen Constellation 19.320 Titan tractor unit, at the 2006 IAA Nutzfahrzeuge (Commercial Vehicles show) in Hannover Right-hand drive Volkswagen Constellation 19.320 Titan in South Africa, January 2016...

Otomegē Sekai wa Mobu ni Kibishii Sekai DesuGambar sampul volume pertama menampilkan Olivia (kiri) dan Leon Fou Bartfort (kanan).乙女ゲー世界はモブに厳しい世界です(Otomegē Sekai wa Mobu ni Kibishii Sekai Desu)GenreKomedi, Isekai, Fiksi Ilmiah[1] Seri novelPengarangYomu MishimaPenerbitShōsetsuka ni NarōTerbit1 Oktober 2017 (2017-10-01) – 15 Oktober 2019 (2019-10-15) Novel ringanPengarangYomu MishimaIlustratorMondaPenerbitMicro MagazinePenerbit bahasa In...

American whiskey liqueur beverage For other uses, see Southern Comfort (disambiguation). Southern ComfortSouthern ComfortTypeLiqueurManufacturerSazerac CompanyCountry of origin United StatesIntroduced1874Proof (US)100, 80, 70, 60, 42Websitesoutherncomfort.com Southern Comfort (often abbreviated SoCo) is an American, naturally fruit-flavored, whiskey liqueur[1] with fruit and spice accents.[2][3][4][5] The brand was created by bartender Martin Wilke...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: American Girl video game series – news · newspapers · books · scholar · JSTOR (October 2017) (Learn how and when to remove this template message) Video game seriesAmerican GirlGenre(s)Edutainment, AdventureDeveloper(s) Various, including The Learning Compa...

Naval forces of the Kingdom of Sardinia, from 1720 to 1861 Royal Sardinian NavyEnsign of the Royal Sardinian Navy from 1816 to 1848Founded1720Disbanded1861Country Kingdom of SardiniaTypeNavyRoleNaval warfareEngagements Battle of Tripoli First Italian War of Independence Second Italian War of Independence Military unit The Royal Sardinian Navy was the naval force of the Kingdom of Sardinia. The fleet was created in 1720 when the Duke of Savoy, Victor Amadeus II, became the King of Sardini...

Katedral SilayPro-Katedral San Diego, SilaySpanyol: Procatedral de San DiegoKatedral Silay10°48′01″N 122°58′33″E / 10.800153°N 122.975839°E / 10.800153; 122.975839Koordinat: 10°48′01″N 122°58′33″E / 10.800153°N 122.975839°E / 10.800153; 122.975839LokasiSilay, Negros OccidentalNegara FilipinaDenominasiGereja Katolik RomaSejarahTanggal konsekrasi1776ArsitekturStatusProkatedralStatus fungsionalaktifArsitekLucio Bern...

Enfermedad de Carrión Hombre con la enfermedad de Carrión, 1898.Especialidad infectología[editar datos en Wikidata] La enfermedad de Carrión, fiebre de La Oroya o verruga peruana es una enfermedad infecciosa endémica de América del Sur, encuadrada dentro de las bartonelosis, cuyo agente etiológico es la bacteria Bartonella bacilliformis. Se debe su nombre al mártir de la medicina peruana, Daniel Alcides Carrión.[1] Historia Verruga peruana Huaco de Áncash, que repre...

Prison centre in Delhi, India For other uses, see Tihar (disambiguation). Tihar JailLocation in DelhiShow map of DelhiLocation in IndiaShow map of IndiaLocationTihar Village, New Delhi, IndiaCoordinates28°37′03″N 77°06′02″E / 28.61750°N 77.10056°E / 28.61750; 77.10056StatusOperatingSecurity classMaximumCapacity10,026Population19,500 [1] (as of 31 December 2022)Opened1957Managed byDepartment of Delhi Prisons, Government of DelhiWebsitetiharprison...

Bell X-22 adalah V/STOL X-plane Amerika Serikat dengan empat kipas miring. X-22 adalah untuk memberikan wawasan yang lebih dalam aplikasi taktis vertikal take-off transporter pasukan seperti pengganti sebelumnya Hiller X-18 dan X-22, Bell XV-15. Persyaratan Program lain adalah kecepatan udara benar di tingkat penerbangan minimal 525 km / h (326 mph, 283 knot). Referensi Apostolo, Giorgio. The Illustrated Encyclopedia of Helicopters. New York: Bonanza Books, 1984. ISBN 0-517-43935-2. Bell-X22A...

Chinese film Soul SnatcherTheatrical release posterTraditional Chinese赤狐書生Simplified Chinese赤狐书生Hanyu PinyinChì hú shūshēng Directed bySong HaolinYi LiqiScreenplay byRan JiananLi HuiyanYang WeiweiBased onChun Jiang Hua Yue Yeby Duo DuoProduced byJiang ZhiqiangJayce ShiFan Kim HungSammi ChanRaman Hui[1]StarringChen LinongLi XianHanikeziJiang ChaoPei KuishanChang Chen-kuangLi XiaochuanCinematographyChan Chi YingEdited byZhang QiMusic byJoe Hisaishi[2]Pro...

1997-2001 Government the United Kingdom This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2017) (Learn how and when to remove this template message) First Blair ministryCabinet of the United Kingdom1997–2001Blair in 1997Date formed2 May 1997 (1997-05-02)Date dissolved8 June 2001 (2001-06-08)People and organisationsMonarchEli...

2014 studio album by LordiScare Force OneStudio album by LordiReleased31 October 2014 (2014-10-31)Genre Hard rock heavy metal shock rock Length48:08LabelAFM RecordsProducerMikko KarmilaLordi chronology To Beast or Not to Beast(2013) Scare Force One(2014) Monstereophonic (Theaterror vs. Demonarchy)(2016) Singles from Scare Force One Nailed by the Hammer of FrankensteinReleased: 19 September 2014 Scare Force One is the seventh studio album by Finnish rock band Lordi. It w...

Come leggere il tassoboxCorydoras imitator Stato di conservazione Specie non valutata Classificazione scientifica Dominio Eukaryota Regno Animalia Sottoregno Eumetazoa Superphylum Deuterostomia Phylum Chordata Subphylum Vertebrata Classe Actinopterygii Sottoclasse Neopterygii Infraclasse Teleostei Superordine Ostariophysi Famiglia Callichthyidae Genere Corydoras Specie C. imitator Nomenclatura binomiale Corydoras imitatorNijssen & Isbrücker, 1983 Corydoras imitator Nijssen & Isbrück...