Cube-connected cycles
|
Read other articles:

Swiss politician Arnold KollerMember of the Swiss Federal CouncilIn office1986–1999Preceded byKurt FurglerSucceeded byRuth MetzlerPresident of SwitzerlandIn office1 January 1997 – 31 December 1997Preceded byJean-Pascal DelamurazSucceeded byFlavio CottiIn office1 January 1990 – 31 December 1990Preceded byJean-Pascal DelamurazSucceeded byFlavio Cotti Personal detailsBornArnold Koller (1933-08-29) 29 August 1933 (age 90)St. Gallen, Switzerland[1]Political par...

International conference in New Hampshire, US in 1944 Mount Washington Hotel The Bretton Woods Conference, formally known as the United Nations Monetary and Financial Conference, was the gathering of 730 delegates from all 44 allied nations at the Mount Washington Hotel, in Bretton Woods, New Hampshire, United States, to regulate the international monetary and financial order after the conclusion of World War II.[1] The conference was held from July 1 to 22, 1944. Agreements were sign...
جزء من سلسلة مقالات حولفيزياء نوويةنشاط إشعاعي • انشطار نووي • اندماج نووي اضمحلال تقليدي تحلل ألفا تحلل بيتا أشعة غاما اضمحلال متطور اضمحلال بيتا المضاعف Double electron capture تحول داخلي متماكب نووي اضمحلال عنقودي انشطار تلقائي عمليات الانبعاث انبعاث النيترونات تفكك بوزيتروني...

李芷晴攝於2020年4月女艺人罗马拼音Lee Tsz Ching英文名Stephanie Lee昵称Step、六合彩女神、幸運女神丶Elaine国籍 中华人民共和国(香港)民族漢族籍贯廣東省出生 (1993-02-06) 1993年2月6日(30歲) 英屬香港职业節目主持、演員、設計師、視覺藝術導師语言粵語、英語、國語教育程度設計學副學士(視覺傳達設計)藝術系學士母校天主教善導小學聖母玫瑰書院玫瑰崗學校香港專上學

Музейно-меморіальний комплекс «Рідна хата» Патріярха Йосифа Сліпого Музей-садиба Йосипа Сліпого Відреставрована хата 49°20′49″ пн. ш. 25°31′19″ сх. д. / 49.34694° пн. ш. 25.52194° сх. д. / 49.34694; 25.52194Координати: 49°20′49″ пн. ш. 25°31′19″ сх. д....

Artikel atau bagian mungkin perlu ditulis ulang agar sesuai dengan standar kualitas Wikipedia. Anda dapat membantu memperbaikinya. Halaman pembicaraan dari artikel ini mungkin berisi beberapa saran.Kontributor utama artikel ini tampaknya memiliki hubungan dekat dengan subjek. Artikel ini mungkin memerlukan perapian untuk mematuhi kebijakan konten Wikipedia, terutama dalam hal sudut pandang netral. Silakan dibahas lebih lanjut di halaman pembicaraan artikel ini. Qoala PT Archor Teknologi Digit...

1998 video gameChina: The Forbidden CityDeveloper(s)Cryo Interactive EntertainmentPublisher(s)Cryo Interactive Entertainment Canal+ Multimedia Réunion des Musées NationauxProducer(s)Alain Le Diberder Platform(s)Windows, PlayStationRelease1998Genre(s)AdventureMode(s)Single-player China: The Forbidden City (French: Chine: Intrigue dans la Cité interdite) is a 1998 adventure video game developed by Cryo Interactive Entertainment and jointly-published by Cryo, Canal+ Multimedia and the R�...

Разом або ніякNous trois ou rien Жанр КомедіяДрамаРежисер Керон ТабібПродюсер Саймон ІстолененСценарист Керон ТабібУ головних ролях Керон ТабібЛейла БехтіОператор Жан-Франсуа ГенсгенсМонтаж Анні ДаншКінокомпанія Adama PicturesGaumontM6 FilmsТривалість 102 хвилиниМова французькаКраїна &#...

Mendelssohn en 1830. La Sinfonía n.º 4 en la mayor, Op. 90 (MWV N 16), también conocida como Italienische Sinfonie o Sinfonía italiana, fue compuesta por Felix Mendelssohn en 1833.[1][2][3] Historia Composición La trayectoria de Mendelssohn en el género sinfónico había comenzado en su adolescencia con la Sinfonía n.º 1 Op. 11 finalizada en 1824 con 15 años. A partir de esta obra la cronología de composición no se corresponde con la numeración de las sinfoní...

Pakistani organization for women's rights This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Aurat Foundation – news · newspapers · books · scholar · JSTOR (September 2017) (Learn how and when to remove this template message) Logo of Aurat Foundation Aurat Foundation, founded in 1986, is a women's rights organi...

Greek Greco-Roman wrestler Stelios MygiakisPersonal informationBorn (1952-05-05) 5 May 1952 (age 71)Rethymno, GreeceHeight1.67 m (5 ft 5+1⁄2 in)Weight62 kg (137 lb)SportSportWrestlingEventGreco-Roman Medal record Men's Greco-Roman Wrestling Representing Greece Olympic Games 1980 Moscow 62 kg European Championships 1979 Bucharest 62 kg Mediterranean Games 1975 Algiers 62 kg 1979 Split 62 kg 1983 Casablanca 62 kg Stelios Mygiaki...

5th episode of the 1st season of The Mandalorian Chapter 5: The GunslingerThe Mandalorian episodePromotional posterEpisode no.Season 1Episode 5Directed byDave FiloniWritten byDave FiloniProduced byJon FavreauCinematography byBarry Baz IdoineEditing by Andrew S. Eisen Dana E. Glauberman Original release dateDecember 6, 2019 (2019-12-06)Running time32 minutesCo-starring Amy Sedaris as Peli Motto Ming-Na Wen as Fennec Shand Jake Cannavale as Toro Calican Episode chronology �...

布蘭登·艾克出生 (1961-07-04) 1961年7月4日(62歲) 美國匹茲堡賓夕法尼亞州母校伊利諾伊大學厄巴納-香檳分校知名于JavaScript网站brendaneich.com 布蘭登·艾克(英語:Brendan Eich,1961年7月4日—)[1],美國程式技术专家與企業家,JavaScript主要創造者與架構師,曾任Mozilla公司的技術長,並曾短暫擔任執行長[2]。 生平 布蘭登·艾克生於美國加州的森尼維爾市,在聖塔�...

2013 YouTube Music AwardsSponsored byKiaDateSunday, November 3, 2013LocationPier 36, New York CityHosted byJason Schwartzman and Reggie WattsTelevision/radio coverageNetworkYouTube YouTube Music Awards · 2015 → The 2013 YouTube Music Awards, abbreviated as the YTMA, was the inaugural music award show presented by YouTube. The inaugural award show was held on November 3, 2013, streamed live from Pier 36 in New York City, with additional shows in Seoul, Moscow, Rio de Janeiro, ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cheech Wizard – news · newspapers · books · scholar · JSTOR (July 2010) (Learn how and when to remove this template message) Comics character Cheech WizardCheech Wizard, in a characteristic discussion of the search for God; art by Vaughn Bodé.Publication infor...

2009 Japanese filmCrayon Shin-chan the Movie: Roar! Kasukabe Animal KingdomTheatrical release posterKanjiクレヨンしんちゃん オタケベ!カスカベ野生王国Revised HepburnKureyon Shinchan: Otakebe! Kasukabe Yasei Ōkoku Directed byAkira ShiginoWritten byYoshito UsuiScreenplay byIsao ShizuyaProduced byYuki YoshidaAtsushi KajiRika TsuruzakiKensuke SuzukiStarringAkiko YajimaMiki NarahashiKeiji FujiwaraSatomi KōrogiCinematographyToshiyuki UmedaEdited byToshihiko KojimaMusic byKei W...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari List of accolades received by Coco (2017 film) di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda mengu...
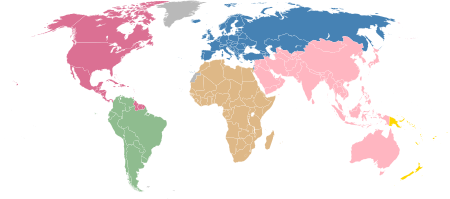
2020 AFC Futsal Championship qualificationTournament detailsHost countriesVietnam (ASEAN)Iran (Central & South)China (East)Bahrain (West)Dates16–27 October 2019[1]Teams31 (from 1 confederation)Tournament statisticsMatches played52Goals scored371 (7.13 per match)Attendance28,992 (558 per match)Top scorer(s) Muhammad Osamanmusa (7 goals)← 2018 2022 → International football competition The 2020 AFC Futsal Championship qualification was the qualificat...

The Mortal Instruments :La Cité des ténèbres Logo français du film. Données clés Titre québécois La Cité des ténèbres : La Coupe Mortelle Titre original The Mortal Instruments: City of Bones Réalisation Harald Zwart Scénario Jessica Postigod'après La Cité des ténèbres : La Coupe Mortelle de Cassandra Clare Acteurs principaux Lily CollinsJamie Campbell BowerRobert SheehanJemima WestKevin ZegersJonathan Rhys MeyersLena Headey Sociétés de production Constantin F...

You can help expand this article with text translated from the corresponding article in Japanese. (December 2009) Click [show] for important translation instructions. View a machine-translated version of the Japanese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English W...

