CourantвҖ“FriedrichsвҖ“Lewy condition
|
Read other articles:
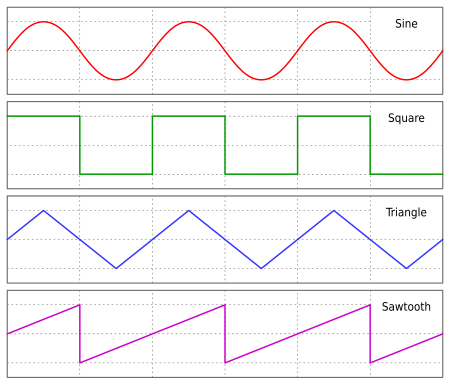
Untuk kegunaan lain, lihat Bentuk gelombang (disambiguasi). Bentuk gelombang sinus, persegi, segitiga, dan gigi gergaji Gelombang sinus, persegi, dan gelombang gigi gergaji pada frekuensi 440 Hz Bentuk gelombang komposit seperti tetesan air Bentuk gelombang yang dihasilkan oleh penyintesis Dalam elektronika, akustika, dan sebagainya, bentuk gelombang dari sebuah sinyal berbentuk grafik sebagai fungsi terhadap waktu.[1][2] Dalam elektronika, istilah bentuk gelombang biasanya di...

ШЈЩ„ШЁШұШӘЩҲ ШҘЩҶШӘШұЩҠШұЩҠЩҲШі Щ…Ш№Щ„ЩҲЩ…Ш§ШӘ ШҙШ®ШөЩҠШ© Ш§ШіЩ… Ш§Щ„ЩҲЩ„Ш§ШҜШ© (ШЁШ§Щ„ШҘШіШЁШ§ЩҶЩҠШ©: Alberto EntrerrГӯos RodrГӯguez)вҖҸ Ш§Щ„Щ…ЩҠЩ„Ш§ШҜ 7 ЩҶЩҲЩҒЩ…ШЁШұ 1976 (Ш§Щ„Ш№Щ…Шұ 47 ШіЩҶШ©)ШҘШіШЁШ§ЩҶЩҠШ§ Ш§Щ„Ш·ЩҲЩ„ 1.92 Щ… (6 ЩӮШҜЩ… 4 ШЁЩҲШөШ©) Щ…ШұЩғШІ Ш§Щ„Щ„Ш№ШЁ ШёЩҮЩҠШұ [Щ„ШәШ§ШӘ ШЈШ®ШұЩү] Ш§Щ„Ш¬ЩҶШіЩҠШ© ШҘШіШЁШ§ЩҶЩҠ Ш§Щ„ЩҲШІЩҶ 102 ЩғЩҠЩ„ЩҲШәШұШ§Щ… (225 ШұШ·Щ„) ШЈШ®ЩҲШ© ЩҲШЈШ®ЩҲШ§ШӘ ШұШ§ШӨЩҲЩ„ ШҘЩҶШӘШұЩҠШұЩҠЩҲШі Ш§Щ„ШӯЩҠШ§Ш© Ш§Щ...

РҹР»СҸР¶ РҹСҖРөРІРөліΠПҒОӯОІОөО»О· ЗагалСҢРҪР° С–РҪС„РҫСҖРјР°СҶС–СҸ 35В°09вҖІ07вҖі РҝРҪ. СҲ. 24В°28вҖІ26вҖі СҒС…. Рҙ. / 35.152222220027773858В° РҝРҪ. СҲ. 24.47388889002778001В° СҒС…. Рҙ. / 35.152222220027773858; 24.47388889002778001РҡРҫРҫСҖРҙРёРҪР°СӮРё: 35В°09вҖІ07вҖі РҝРҪ. СҲ. 24В°28вҖІ26вҖі СҒС…. Рҙ. / 35.152222220027773858В° РҝРҪ. СҲ. 24.47388889002778001В° СҒС…. ...

El texto que sigue es una traducciГіn defectuosa. Si quieres colaborar con Wikipedia, busca el artГӯculo original y mejora esta traducciГіn.Copia y pega el siguiente cГіdigo en la pГЎgina de discusiГіn del autor de este artГӯculo: {{subst:Aviso mal traducido|CrГӯmenes de guerra alemanes}} ~~~~ El gueto de Varsovia вҖ“ Foto del informe de JГјrgen Stroop a Heinrich Himmler a partir de mayo de 1943. El tГӯtulo original en alemГЎn dice: Por la fuerza se retiraron de refugios subterrГЎneos. La Гәn...

JB12Stasiun SendagayaеҚғ駄гӮұи°·й§…Pintu masuk Stasiun Sendagaya pada bulan Juni 2020Lokasi1 Sendagaya, Shibuya, TokyoпјҲжқұдә¬йғҪжёӢи°·еҢәеҚғ駄гғ¶и°·1дёҒзӣ®пјүJepangPengelolaJR EastJalurJB Jalur ChЕ«ЕҚ-SЕҚbuSejarahDibuka1904PenumpangFY201120,008 per hari Operasi layanan Stasiun sebelumnya JR East Stasiun berikutnya YoyogiJB11kearah Mitaka Jalur ChЕ«ЕҚвҖ“SЕҚbu ShinanomachiJB13kearah Chiba Sunting kotak info вҖў L вҖў BBantuan penggunaan templat ini Stasiun Sendagaya (еҚғ駄гӮұи°·й...

VГ©anse tambiГ©n: Eurovision y Eurozona. Una bolsa con las primeras monedas de euro de Eslovaquia en ser fabricadas. El euro (EUR o вӮ¬) es la moneda oficial de las instituciones de la UniГіn Europea desde 1999 (cuando sustituyГі al ECU), de los Estados que pertenecen a la eurozona[1][2] y de los micro-Estados europeos con los que la UniГіn tiene acuerdos al respecto. TambiГ©n es utilizado de facto en Montenegro y Kosovo.[3] Las monedas de euro estГЎn diseГұadas ...

Ш§Щ„ШЁШұЩҲШӘШіШӘШ§ЩҶШӘЩҠШ© Ш§Щ„Ш®Ш· Ш§Щ„ШұШҰЩҠШіЩҠ ШЈЩҲ Ш§Щ„ШЁШұЩҲШӘШіШӘШ§ЩҶШӘЩҠШ© Ш§Щ„ШӘЩӮЩ„ЩҠШҜЩҠШ© ЩҮЩҲ Щ…ШөШ·Щ„Шӯ ШҙШ§ШҰШ№ ЩҒЩҠ Ш§Щ„ЩҲЩ„Ш§ЩҠШ§ШӘ Ш§Щ„Щ…ШӘШӯШҜШ© Щ„ЩҲШөЩҒ Ш§Щ„ЩғЩҶШ§ШҰШі Ш§Щ„ШЁШұЩҲШӘШіШӘШ§ЩҶШӘЩҠШ© Ш§Щ„ШӘЩӮЩ„ЩҠШҜЩҠШ© ЩҲШ§Щ„ШӘЩҠ ШӘШҙЩ…Щ„ ШіШЁШ№ Щ…Ш°Ш§ЩҮШЁ ЩҲЩҮЩҠ Ш§Щ„Щ…ШҙЩҠШ®ЩҠШ©ШҢ ЩҲШ§Щ„ШЈШЁШұШҙШ§ЩҶЩҠШ©ШҢ ЩҲШ§Щ„ШЈШіЩӮЩҒЩҠШ©ШҢ ЩҲШ§Щ„Щ…ЩҠШ«ЩҲШҜЩҠШ©ШҢ ЩҲШ§Щ„Щ„ЩҲШ«ШұЩҠШ©ШҢ ЩҲШ§Щ„Щ…Ш№Щ…ШҜШ§ЩҶЩҠШ© ЩҲЩ„ЩҮШ°ЩҮ Ш§Щ„Щ…Ш°Ш§ЩҮШЁ ЩӮШ§Ш№ШҜШ© Ш§Ш¬ШӘЩ…Ш§Ш№ЩҠШ© Ш№ШұЩҠШ¶Ш© ШұШ§ШіШ®Ш© ЩҒЩҠ Ш§Щ„Ш...

гғ•гӮёгғ»гғЎгғҮгӮЈгӮўгғ»гғӣгғјгғ«гғҮгӮЈгғігӮ°гӮ№ > гғқгғӢгғјгӮӯгғЈгғӢгӮӘгғі гҒ“гҒ®й …зӣ®гҒҜз”»еғҸж”№иЁӮдҫқй јгҒ«еҮәгҒ•гӮҢгҒҰгҒҠгӮҠгҖҒ2004е№ҙгҒӢгӮү2016е№ҙгҒҫгҒ§гҒ®гғӯгӮҙгғһгғјгӮҜгӮ’й«ҳи§ЈеғҸеәҰзүҲгҒЁгҒҷгӮӢгӮҲгҒҶз”»еғҸж”№иЁӮгҒҢжұӮгӮҒгӮүгӮҢгҒҰгҒ„гҒҫгҒҷгҖӮпјҲ2023е№ҙ5жңҲпјү ж ӘејҸдјҡзӨҫгғқгғӢгғјгӮӯгғЈгғӢгӮӘгғіPONY CANYON INC. жң¬зӨҫгҒҢе…Ҙеұ…гҒҷгӮӢжіүгӮ¬гғјгғҮгғіANNEXзЁ®йЎһ ж ӘејҸдјҡзӨҫз•Ҙз§° PCгҖҒгғқгғӢгӮӯгғЈгғіпјҲгҒҪгҒ«гҒҚгӮғгӮ“пјүжң¬зӨҫжүҖеңЁең° ж—Ҙжң¬гҖ’106-8487жқұдә¬йғҪжёҜеҢәе…ӯжң¬жңЁд...

Official flags of the U.S. city of New York City City of New YorkAdoptedApril 6, 1915(modified December 30, 1977)DesignA vertical tricolor of blue, white, and orange with a modified blue version of the Seal of New York City in the center. The flag unfurled and fluttering, mounted on a city park yardarm The flags of New York City include the flag of New York City, the respective flags of the boroughs of The Bronx, Brooklyn, Manhattan, Queens, and Staten Island, and flags of certain city depart...

Covaxin Covaxin (tГӘn mГЈ lГ BBV152) lГ mб»ҷt loбәЎi vбәҜc xin COVID-19 dб»ұa trГӘn virus bбәҘt hoбәЎt Д‘Ж°б»Јc Bharat Biotech phб»‘i hб»Јp vб»ӣi Hб»ҷi Д‘б»“ng NghiГӘn cб»©u Y khoa бәӨn Дҗб»ҷ phГЎt triб»ғn. Hiб»Үu quбәЈ VГ o thГЎng 7 nДғm 2021, Bharat Biotech bГЎo cГЎo vбәҜc xin cГі hiб»Үu quбәЈ 64% Д‘б»‘i vб»ӣi cГЎc trЖ°б»қng hб»Јp khГҙng cГі triб»Үu chб»©ng, 78% hiб»Үu quбәЈ Д‘б»‘i vб»ӣi cГЎc trЖ°б»қng hб»Јp cГі triб»Үu chб»©ng, 93% hiб»Үu quбәЈ chб»‘ng lбәЎi nhiб»…m COVID-19 nghiГӘm trб»...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sega Heroes вҖ“ news В· newspapers В· books В· scholar В· JSTOR (November 2023) (Learn how and when to remove this template message) 2018 video gameSega HeroesCover artwork of Sega Heroes, featuring (from left to right) Gum, Werebear, and ChuPeaDeveloper(s)Demiurge S...

Railway station in Minamiashigara, Kanagawa Prefecture, Japan Fujifilm-Mae StationеҜҢеЈ«гғ•гӮӨгғ«гғ еүҚй§…Fujifilm-Mae Station, March 2014General informationLocation60-1 Kano, Minamiashigara-shi, Kanagawa-ken 250-0126JapanCoordinates35В°19вҖІ3.6вҖіN 139В°6вҖІ32.0вҖіE / 35.317667В°N 139.108889В°E / 35.317667; 139.108889Operated by Izuhakone RailwayLine(s) DaiyЕ«zan LineDistance9.1 km from Odawara.Platforms1 side platformConnections Bus stop Other informationStation...

LighthouseGros Cap Reefs Light LocationSault Ste. Marie Ontario CanadaCoordinates46В°30вҖІ42вҖіN 84В°36вҖІ53вҖіW / 46.51167В°N 84.61472В°W / 46.51167; -84.61472TowerConstructionskeletal towerHeight18 metres (59 ft)Shapeskeletal mast on a three-story keeper's quartersMarkingswhite tower with red trimOperatorCanadian Coast Guard[1]LightFirst lit1953Focal height18 metres (59 ft)Range12 nautical miles (22 km; 14 mi)CharacteristicFl R 5s. The...

3rd-century Roman Christian saint For the holiday, see Valentine's Day. For the Canadian city, see Saint-Valentin, Quebec. For the song, see Saint Valentine (song). For other uses of San Valentino, see San Valentino (disambiguation). Not to be confused with Valentinus (Gnostic) or Valentine of Passau. SaintValentineSaint Valentine is healing an epilepsy illustrated by Dr. FrantiЕЎek Ehrmann, circa 1899.Bishop of Terni and MartyrBornc. 226Terni, Italia, Roman EmpireDiedc. 269 (aged...

Autobiography by Doan Van Toai Le Goulag Vietnamien(First edition) First editionAuthorDoan Van Toai, as told to Michel VoirolCountryFranceLanguageFrenchGenreAutobiographyPublished1979PublisherParis : R. LaffontMedia typePrintPages341 p.ISBN2-221-00385-3OCLC476545048 The Vietnamese Gulag(First English translation) AuthorDoan Van Toai, David ChanoffOriginal titleLe Goulag VietnamienTranslatorSylvie Romanowski and Françoise Simon-Miller.Countrytr. from FranceLanguagetr. from Fren...

Railway between Port Augusta, South Australia and Kalgoorlie, Western Australia For the former passenger train between Western Australia and South Australia, see Trans-Australian. Trans-Australian Railway Route map Legend km Adelaide-Port Augusta line 0 Port Augusta branch line to Whyalla 28 Tent Hill 55 Hesso 85 Bookaloo 118 McLeay 150 Wirrappa 181 Pimba branch line to Woomera 219 Burando 250 Wirraminna 283 Coondambo 302 Kultanaby 335 Kingoonya 377 Ferguson 413 Tarcoola TarcoolaвҖ“Darw...

Stax RecordsLogo Stato Stati Uniti Fondazione1957 Fondata daStewart / Axton Sede principaleMemphis GruppoConcord Bicycle Music SettoreMusicale ProdottiSoul Sito webwww.staxrecords.com/ Modifica dati su Wikidata В· Manuale La Stax Records ГЁ una etichetta discografica statunitense, fondata a Memphis nel 1957 con il nome di Satellite Records. CambiГІ nome in Stax Records nel 1961, e fu in attivitГ fino al 1976, anno nel quale chiuse per bancarotta. Il nome Stax ГЁ la crasi dei cognom...

Untuk kegunaan lain, lihat Maza. Maza Maza Revolusibumilangit.fandom.com Penerbit Bumilangit Komik Munculperdana 2017 Pencipta Harya Suraminata (Hasmi) Karakteristik Nama KarakterImajiSpesiesManusiaAfiliasikelompokJagabumiRekan perjuanganGodam Revolusi Aquanus Revolusi Sri Asih Revolusi Gundala Revolusi MandalaKemampuan Kekuatan super Memiliki Gelang yang dapat muncul jin (Jin Kartubi) yang tunduk atas perintahnya Dan merasuk kedalam mimpi Maza adalah tokoh superhero komik ciptaan Hasmi. Munc...

Questa voce o sezione sull'argomento musicisti britannici non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Jimmy Bain NazionalitГ Regno Unito GenereHeavy metalHard rock Periodo di attivitГ musicale1974 вҖ“ 2016 GruppiRainbow, Dio, WWIII, 3 Legged Dogg, Last in Line Album pubblicati...

16 RhagfyrEnghraifft o'r canlynolpwynt mewn amser mewn perthynas ag amserlen gylchol Math16th Rhan oRhagfyr Ffeiliau perthnasol ar Gomin Wicimedia << Rhagfyr >> Ll Ma Me Ia Gw Sa Su 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 2020 Rhestr holl ddyddiau'r flwyddyn 16 Rhagfyr yw'r hanner canfed dydd wedi'r trichant (350fed) o'...
















