Collinearity
|
Read other articles:

Leo VI Påve 928–928NamnLeoFöddokäntDöddecember 928FöreträdareJohannes XEfterträdareStefan VIIPåve i 0 år, 6 månader och 0 dagar Leo VI, född i Rom, död i december 928, var påve från maj eller juni 928 till sin död. Biografi Leo var romare och son till den romerske primicerius Christophorus, som hade varit Johannes VIII:s premiärminister. Innan Leo blev påve var han kardinalpräst med Santa Susanna som titelkyrka. Det råder viss osäkerhet om den exakta dateringen av Leos p...

2003 studio album by Don McLeanThe Western AlbumStudio album by Don McLeanReleased2003GenreRockLength40:03LabelDon McLean RecordsDon McLean chronology You've Got to Share: Songs for Children(2003) The Western Album(2003) Christmastime!(2004) Professional ratingsReview scoresSourceRatingAllmusic [1] The Western Album is an album by American singer-songwriter Don McLean, released in 2003. Track listing Timber Trail (Tim Spencer) – 3:01 Ridin' Down the Canyon (Gene Autry, S. Bu...

Ця стаття не містить посилань на джерела. Ви можете допомогти поліпшити цю статтю, додавши посилання на надійні (авторитетні) джерела. Матеріал без джерел може бути піддано сумніву та вилучено. (серпень 2021) Збройні сили Афганістану Засновані 1709Поточна форма 2002Види зброй

Usuario en silla de ruedas entrando a una parada de autobús elevada en Curitiba, Brasil.Los productos de apoyo para la movilidad son dispositivos diseñados con el propósito de asistir al caminar o de mejorar la movilidad de las personas con discapacidad motora. Existen diferentes productos que pueden ayudar a las personas con deterioro de la habilidad para caminar, como sillas de ruedas o scooters eléctricos para discapacidades más graves o viajes más largos que de otro modo se realizar...

Pemilihan umum Bupati Pasaman Barat 20242020202927 November 2024Kandidat Peta persebaran suara Peta Sumatera Barat yang menyoroti Kabupaten Pasaman Barat Bupati petahanaHamsuardi Partai Amanat Nasional Bupati terpilih belum diketahui Sunting kotak info • L • BBantuan penggunaan templat ini Pemilihan umum Kabupaten Pasaman Barat 2024 (selanjutnya disebut Pilkada Pasaman Barat 2024 atau Pilbup Pasaman Barat 2024) dilaksanakan pada 27 November 2024 untuk memilih Bupati Pasaman Bara...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Benteng Pulau Penyengat adalah benteng yang berada di Pulau Penyengat, Kota Tanjungpinang, Kepulauan Riau, Indonesia. Nilai sejarah dari kompleks bendeng ini adalah peperangan antara Kesultanan Lingga dengan Belanda. Kegunaan seluruh benteng ini sebaga...

Bambang SukarnoBupati Temanggung 22Masa jabatan2013 – 2018PresidenSusilo Bambang YudhoyonoJoko WidodoGubernurBibit WaluyoGanjar PranowoBupati Temanggung|WakilIrawan PrasetyadiPendahuluHasyim AfandiPenggantiMuhammad Al Khadziq Informasi pribadiLahir18 Februari 1954Magelang, Jawa TengahKebangsaanIndonesiaPartai politikPDI PerjuanganSunting kotak info • L • B Drs. HM. Bambang Sukarno (lahir 18 Februari 1954) adalah bupati Temanggung yang menjabat pada periode 2013-20...

Reet SharmaReet Sharma pada 2014Lahir12 Februari 2005 (umur 18)New Delhi, IndiaKebangsaanIndiaPekerjaanArtis cilikTahun aktif2009–sekarangTinggi5 ft 0 in (1,52 m) Reet Sharma adalah seorang aktris cilik India yang biasanya berkarya dalam sinema Hindi dan sinetron. Ia telah tampil dalam film-film yakni Dabangg 2 dan Maximum Movie. Ia tampil dalam acara-acara Televisi seperti Gumrah: End of Innocence (musim 4).[1] Ia sekarang tampil dalam sinetron Star Plus Is...

Franchise of book, film, and TV series This article is about the media franchise. For other uses, see Mash (disambiguation). M*A*S*HThe fingerpost from the M*A*S*H set, as seen in the Smithsonian Institution[1]Created byRichard HookerOriginal workMASH: A Novel About Three Army Doctors (1968)Owner20th Century StudiosYears1968–1986Print publicationsNovel(s)List of novels (1968–1977)Films and televisionFilm(s)M*A*S*H (1970)Television series M*A*S*H (1972–1983) Trapper John, M.D. (1...

Genus of corals Schizocyathus D = calyx from aboveE = lateral view Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Cnidaria Class: Hexacorallia Order: Scleractinia Family: Schizocyathidae Genus: SchizocyathusPourtalès, 1874 [2] Species: S. fissilis Binomial name Schizocyathus fissilisPourtalès, 1874 [1] Schizocyathus is a monotypic genus of stony corals in the family Schizocyathidae, the only species being Schizocyathus fissilis. It is a deep water...

Unique identifier of a firearm The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (November 2020) (Learn how and when to remove this template message) The serial number of this pistol is located under the dust cover on the frame, on the barrel, and on the slide. The bolt of an Arisaka military rifle, which carries identifiers matching the main...

Hajime Waki Hajime Waki (脇一, born in 1999) is a Honduran-Japanese singer-songwriter of Bachata music that gained popularity after playing and composing songs of this genre in Japanese. He is the first artist who composes mixing this three languages altogether in one song (Japanese, English, Spanish). He has a mixture of cultures there being born in Honduras and his mother being a Japanese Dominican. Biography He was born and raised in the city of Comayagua in Honduras, his father is from ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bhopal Express film – news · newspapers · books · scholar · JSTOR (November 2018) (Learn how and when to remove this template message) 1999 Indian filmBhopal ExpressDVD cover of Bhopal ExpressDirected byMahesh MathaiWritten byPrasoon PandeyPiyush PandeyPro...
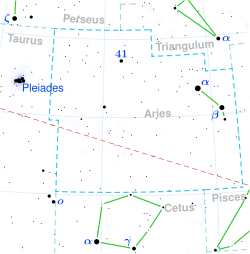
おひつじ座ε星 A / Bε Arietis 星座 おひつじ座 見かけの等級 (mv) 4.63[1](5.17 / 5.57)[2] 位置元期:J2000.0 赤経 (RA, α) 02h 59m 12.7237306183s[3] 赤緯 (Dec, δ) +21° 20′ 25.541697255″[3] 視線速度 (Rv) 0.9 ± 0.9 km/s[4] 固有運動 (μ) 赤経: -14.092 ミリ秒/年[3]赤緯: -7.345 ミリ秒/年[3] 年周視差 (π) 8.5110 ± 0.3418ミリ秒[...

Wildlife and nature charity in United Kingdom The Wildlife TrustsThe Wildlife Trusts headquarters in Newark-on-TrentPredecessorThe Society for the Promotion of Nature ReservesFormation1912; 111 years ago (1912)TypeCharitable trustRegistration no.207238LocationNewark-on-Trent, Nottinghamshire, United KingdomPresidentLiz BonninChairmanDuncan IngramChief ExecutiveCraig BennettWebsitewww.wildlifetrusts.org The Wildlife Trusts, the trading name of the Royal Society of Wildli...

1936 film by Robert Zigler Leonard The Great ZiegfeldTheatrical release posterDirected byRobert Z. LeonardWritten byWilliam Anthony McGuireProduced byHunt StrombergStarringWilliam PowellMyrna LoyLuise RainerCinematographyOliver T. MarshEdited byWilliam S. GrayMusic byWalter DonaldsonLyrics:Harold AdamsonProductioncompanyMetro-Goldwyn-MayerDistributed byLoew's Inc.Release dates March 22, 1936 (1936-03-22) (Los Angeles, premiere) April 8, 1936 (1936-04-08) ...

American rapper This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: YZ rapper – news · newspapers · books · scholar · JSTOR (September 2012) (Learn how and when to remove this template message)...

Бої за Луганський аеропорт Війна на сході України Луганський аеропорт на карті боївЛуганський аеропорт на карті боїв Дата: 8 квітня — 1 вересня 2014 (146 днів) Місце: Міжнародний аеропорт «Луганськ», Луганськ, Луганська область(Переможне, Тернове, Новоганнівка, Красне) Рез�...

1927 film BackstageDirected byPhil GoldstoneWritten bySarah Y. Mason Jack NattefordStarringWilliam Collier Jr. Barbara Bedford Alberta VaughnCinematographyJoseph A. Dubray E. Fox WalkerEdited byLeroy O. LodwigProductioncompanyTiffany PicturesDistributed byTiffany PicturesRelease dateApril 1, 1927Running time65 minutesCountryUnited StatesLanguagesSilent English intertitles Backstage is a 1927 American silent comedy film directed by Phil Goldstone and starring William Collier Jr., Barbara Bedfo...

Peta menggambarkan wilayah abad pertengahan termasuk Béarn Centule III dari Béarn (bahasa Prancis: Centulle III de Béarn; bahasa Latin: Centuli Gastoni) adalah seorang bangsawan Prancis, seorang vicomte di Béarn.[1] Dia adalah putra Vicomte Gaston I dari Béarn dan istrinya yang tidak diketahui namanya dalam sumber-sumber utama[2], dan putra mereka bernama Gaston II, dinamai seperti ayahandanya.[3] Centulle dibunuh oleh Lord Lupus yang Kuat. Dia kemudian digantikan...














