Algebraic topology
|
Read other articles:

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2021) شيفروليه كابريسمعلومات عامةالنوع سيارة عائلية كبيرة العلامة التجارية شيفروليه المصنع جنرال موتورز البلد ا

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) لمعانٍ أخرى، طالع محمد ناصر (توضيح). محمد ناصر احمد علي الحسني وزير الدفاع الجمهورية اليمنية في �...
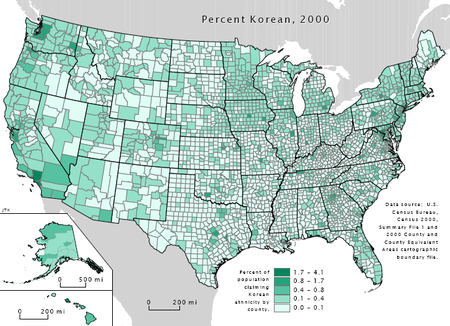
Koreanische Amerikaner (engl. Korean Americans) sind Bürger der Vereinigten Staaten von koreanischer Abstammung. Inhaltsverzeichnis 1 Demografie 2 Bekannte koreanische Amerikaner 3 Siehe auch 4 Weblinks 5 Einzelnachweise Demografie Nach Angaben des United States Census 2010 lebten 1,4 Millionen Koreanische Amerikaner in den Vereinigten Staaten.[1] Die Hauptsiedlungsgebiete der Koreanischen Amerikaner sind Greater Los Angeles Area (334.329) und die New York Metropolitan Area (218.764)...

Формальні науки — сукупність наук, які займаються дослідженням формальних систем. До формальних наук, наприклад, належать: логіка, математика, теоретична інформатика, теорія інформації, теорія систем, теорія рішень, статистика, деякі аспекти мовознавства. Формальні нау�...

Friedrich Wilhelm von Reden F. W. Reden w mundurze Data i miejsce urodzenia 23 marca 1752 Hameln Data i miejsce śmierci 3 lipca 1815 Bukowiec Zawód, zajęcie minister Multimedia w Wikimedia Commons Friedrich Wilhelm von Reden Kaplica grobowa Friedricha Wilhelma von Redena, tzw. „Ruiny Opactwa”, na zboczach Mrowca w Rudawach Janowickich. Friedrich Wilhelm von Reden (ur. 23 marca 1752 w Hameln, zm. 3 lipca 1815 w Bukowcu) – niemiecki dyrektor Wyższego Urzędu Górniczego we W...

2006 Canadian filmMonkey WarfareFilm posterDirected byReginald HarkemaWritten byReginald HarkemaProduced byLeonard FarlingerJennifer JonasKris KingStarringDon McKellarTracy WrightNadia LitzCinematographyJonathon CliffEdited byKathy WinkaufMusic byDJ Hans LucasRelease dates September 10, 2006 (2006-09-10) (TIFF) November 15, 2006 (2006-11-15) (Canada) Running time75 minutesCountryCanadaLanguageEnglish Monkey Warfare is a 2006 Canadian drama film written an...

Appointed head of Sindh, Pakistan Governor of SindhGovernor of Sindh's SealProvincial Flag of SindhIncumbentKamran Tessorisince 9 October 2022StyleThe Honorable(formal)ResidenceGovernor HouseSeatKarachi, Sindh, PakistanNominatorPrime Minister of PakistanAppointerPresident of PakistanTerm length5 yearsConstituting instrumentConstitution of PakistanFormation15 August 1947; 76 years ago (1947-08-15)First holderSir Charles NapierSalary10000$Websitewww.governorsindh.gov.pk T...

Human settlement in EnglandEast MerseaSt Edmund's church, East MerseaEast MerseaLocation within EssexPopulation266 (2011 Census)[1]OS grid referenceTM060150DistrictCity of ColchesterShire countyEssexRegionEastCountryEnglandSovereign stateUnited KingdomPost townColchesterPostcode districtCO5Dialling code01206PoliceEssexFireEssexAmbulanceEast of England UK ParliamentHarwich and North Essex List of places UK England Essex 51°47′45″N 0°59′09...

Batang melenting getar adalah contoh sistem dasar dalam fisika dengan tenaga potensial lenting yang diubah menjadi teng kinetik dan sebaliknya. Dalam fisika, elastisitas atau kelentingan (dari Yunani ἐλαστός ductible) adalah kecenderungan bahan padat untuk kembali ke bentuk aslinya setelah terdeformasi. Benda padat akan mengalami deformasi ketika gaya diterapkan padanya. Jika bahan tersebut elastis, benda tersebut akan kembali ke bentuk dan ukuran awalnya ketika gaya dihilangkan. Alas...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Singles, Volume III: 1964–1965 – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) 2007 compilation album by James BrownThe Singles, Volume III: 1964–1965Compilation album by James BrownReleasedJune 8...

U.S. brand of hot sauce Cholula Hot SauceProduct typeHot sauceOwnerMcCormick & CompanyCountryMexicoWebsiteCholula.com[1] Cholula Hot Sauce is a brand of chili-based hot sauce, based in Stamford, Connecticut, manufactured in Chapala, Jalisco, Mexico by SANE, and licensed by McCormick. According to its manufacturers, Cholula hot sauce rates 1,000–2,000 on the Scoville scale[2] though other sources measure it as being over three times as hot, at 3,600 Scoville units.[3&...

关于与「李佳芯」標題相近或相同的条目,請見「李佳芯 (消歧義)」。 本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目應避免有陳列雜項、瑣碎資料的部分。 (2022年6月22日)請協助將有關資料重新編排成連貫性的文章,安置於適當章節或條目內。 此條目的引用需要进行清理,使其符合格式。 (2023年5月8日)参考文献应符合正确的引用、�...

Hospital in Songkhla, ThailandHatyai Hospital โรงพยาบาลหาดใหญ่Ministry of Public Health Health District 12The Accident and Emergency BuildingGeographyLocation182 Ratthakan Road, Hat Yai District, Songkhla, ThailandCoordinates7°01′00″N 100°28′05″E / 7.01667°N 100.46806°E / 7.01667; 100.46806OrganisationTypeRegionalAffiliated universityFaculty of Medicine, Prince of Songkla UniversityServicesStandardsHospital Accreditation (Ins...

Bukan Sekedar WayangGenreKomediPresenterSuleCepotNegara asalIndonesiaBahasa asliIndonesiaBahasa SundaJmlh. episode577ProduksiProduserBima Indra Sakti Melanie Yoana SihombingDurasi30 menitRumah produksiNET. EntertainmentDistributorNet Mediatama TelevisiIndika Entertainment GroupRilis asliJaringanNET.Format audioDolby Digital 5.1Rilis23 Juni 2014 (2014-06-23) –31 Juli 2016 (2016-7-31)Acara terkaitCanda Wayang (MNCTV)Asep Show (MNCTV)Wayang Kulit (Indosiar)Cepot Show (MNCTV) Buk...

Multiplex cinema hall in Mumbai, India Sterling CineplexSterling Cinema, Sterling TheatreAddress65, Cinema Lane, Marzaban Road, FortMumbaiIndiaCoordinates18°56′17″N 72°49′59″E / 18.938°N 72.833°E / 18.938; 72.833TypeMultiplexConstructionOpened1969Reopened2007Years active1969–presentWebsitehttp://www.sterlingcineplex.in/ Sterling Cineplex (previously known as Sterling Cinema) is a multiplex cinema hall in Mumbai. Opened (as a multiplex) in 2007, Sterling h...

Cathedral city and county town of Cumbria, England This article is about the city in England. For other uses, see Carlisle (disambiguation). City in EnglandCarlisleCityThe city skyline, cathedral, old town hall, citadel and castleCarlisleLocation within CumbriaPopulation74,281 (2021)OS grid referenceNY395555• London261 mi (420 km) SSEUnitary authorityCumberlandCeremonial countyCumbriaRegionNorth WestCountryEnglandSovereign stateUnited KingdomPost...

Bohemian doctor and scientist Jan Marek MarciBorn13 June 1595[1]LanškrounDied10 April 1667 (1667-04-11) (aged 71)[1]PragueNationalityCzechAlma materUniversity of Olomouc, OlomoucCharles University, PragueScientific careerFieldsMedicine, Mechanics, Optics, MathematicsInstitutionsCharles University, Prague Jan Marek Marci FRS (German: Johannes Marcus Marci de Cronland; June 13, 1595–April 10, 1667), or Johannes Marcus Marci, was a Bohemian doctor and scientist,...

Arvo Aaltonen Medallista olímpico Datos personalesNacimiento Pori (Finlandia)2 de diciembre de 1892Nacionalidad(es) Rusa y FinlandesaFallecimiento Pori (Finlandia)17 de junio de 1949Carrera deportivaDeporte Natación Medallero Natación Finlandia Finlandia Juegos Olímpicos BronceAmberes 1920200 m braza BronceAmberes 1920400 m braza [editar datos en Wikidata] Arvo Aaltonen (Pori, 2 de diciembre...

For the Heather Alexander and Alexander James Adams album, see Alexander James Adams. 1996 studio album by Don RossWintertideStudio album by Don RossReleased1996GenreChristmasLabelColumbia/Sony CanadaDon Ross chronology This Dragon Won't Sleep(1995) Wintertide(1996) Loaded, Leather, Moonroof(1997) Wintertide is an album by the Canadian guitarist Don Ross, released in 1996. Reception Professional ratingsReview scoresSourceRatingAllmusic [1] Music critic Roch Parisien, writing f...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. KoprofobiaInformasi umumSpesialisasiPsychology Koprofobia adalah ketakutan atau keengganan untuk buang air besar atau keengganan terhadap feses.[1] Pada manusia, feses dan buang air besar sudah menjadi budaya tabu.[2] Coprophobia atau k...




