نظرية التحكم
|
Read other articles:

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 福岡県警察 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2021年3月) 福岡県の行政機関福岡県警察 福岡県警察本部庁

U-KISS유키스Dari kiri ke kanan: Eli, Dongho, Hoon, AJ, Kiseop, Kevin, SoohyunInformasi latar belakangAsalSeoul, Korea SelatanGenreK-popDanceelectropopTahun aktif2008 (2008)–sekarangLabelNH Media Artis terkaituBEATXINGParanSitus webu-kiss.jpAnggota Soohyun Kiseop Eli Hoon Jun Mantan anggota Alexander Lee Eusebio Kim Kibum Dongho AJ Kevin Templat:Korean membutuhkan parameter |hangul=. U-KISS (bahasa Korea: 유키스, Jepang: ユーキス) adalah boy band Korea Selatan...

Julieta Poggio Información personalApodo Juli, Disney, julaiNacimiento 9 de enero de 2002 (21 años)Buenos Aires, ArgentinaResidencia Buenos Aires, ArgentinaNacionalidad ArgentinaInformación profesionalOcupación Actriz, modelo y bailarinaAños activa 2009-presenteConocida por Participante de Gran HermanoInstrumento Voz [editar datos en Wikidata] Julieta Poggio (Buenos Aires, 9 de enero de 2002) es una modelo, actriz, bailarina y profesora de danza argentina. Luego de su...

Russian-Polish pair skater Dmitri KhrominKhromin and Piątkowska in 2006.Full nameDmitri Vladimirovich KhrominBorn (1982-10-21) October 21, 1982 (age 41)LeningradHeight1.78 m (5 ft 10 in)Figure skating careerCountry PolandPartnerDominika PiątkowskaCoachStanislav Leonovitch, Olga LeonovichSkating clubMKL Lodz Dmitri Vladimirovich Khromin (born October 21, 1982, in Leningrad, Russian SFSR) is a figure skating coach and former Russian-Polish pair skater. He competes wit...

American mobile virtual network operator Pure Talk Holdings, Inc.TypeSubsidiaryIndustryTelecommunicationsFounded2010 (2010)HeadquartersCovington, Georgia, United StatesServicesWireless service providerNumber of employees500+ [2022]ParentTelrite Holdings, Inc.Websitepuretalk.com Pure Talk Holdings, Inc. is an American mobile virtual network operator headquartered in Covington, Georgia, United States with two other offices located in Fort Lee, New Jersey and Atlanta, Georgia. It provides w...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2019) بيتري أندري معلومات شخصية الميلاد 29 يونيو 1891 برايلا الوفاة 4 أكتوبر 1940 (49 سنة) ياش سبب الوفاة تسمم بالسيانيد مواطنة رومانيا الحياة العمل

American musician David Bennett CohenCohen at Summer of Love, Lafayette, California in 2017Background informationBirth nameDavid Bennett CohenBorn (1942-08-04) August 4, 1942 (age 81)Brooklyn, New York, U.S.GenresBluesfolkpsychedelic rockrockragtimeboogie-woogieOccupation(s)MusicianInstrument(s)Guitarpianoelectronic organYears activec. 1959–presentWebsiteOfficial website Musical artist David Bennett Cohen (born August 4, 1942)[1] is an American musician best known as the ...

TrES-4bJenis objekPlanet luar surya, jupiter panas Nama lainTrES-4b, TOI-2124bData pengamatan(Epos J2000.0[*]) Rasi bintangHerkules Asensio rekta268,30437115898960 derajat Deklinasi37,21182947394333 derajat Radius1,61±0,18 radius JupiterMetode penemuanmetode transit[*]Tahun penemuan2006 Media Terkait di Wikimedia Commons[sunting di Wikidata] TrES-4b adalah sebuah planet luar surya yang terletak sekitar 1708 tahun cahaya dari Bumi. Planet ini ditemukan pada tahun 2007 dengan men...
لمعانٍ أخرى، طالع امتصاص (توضيح). هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2022) الامتصاص الجلدي هو...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Akademi Fantasi Indosiar Musim II – berita · surat kabar · buku · cendekiawan · JSTOR satukan tabel, hilangkan pengkoloman, supaya tidak semrawut ini perlu dirapikan agar memenuhi standar Wikipedia. Tida...

All Elite Wrestling pay-per-view event Full GearPromotional poster featuring various AEW wrestlersPromotionAll Elite WrestlingDateNovember 7, 2020CityJacksonville, FloridaCameron, North Carolina[a]VenueDaily's PlaceAttendance1,000[1]Buy rate100,000[2]Tagline(s)Don’t Chase Dreams ... Hunt Goals[3]Pay-per-view chronology ← PreviousAll Out Next →Revolution Full Gear chronology ← Previous2019 Next →2021 The 2020 Full Gear was the secon...

Henry Whitehead (ongeveer 30 jaar oud) John Henry Constantine Whitehead (ook Henry Whitehead) (Chennai 11 november 1904 – Princeton 8 mei 1960), was een Brits wiskundige. Hij was een van de grondleggers van de homotopietheorie. Zie ook Whitehead-schakel Whitehead-variëteit

Convoy during naval battles of the Second World War Convoy ON 166Part of Battle of the AtlanticA depth charge being loaded onto a depth-charge thrower aboard the corvette HMS DianthusDate20–25 February 1943LocationNorth AtlanticResult German tactical victoryBelligerents United Kingdom United States Canada Poland GermanyCommanders and leaders CAPT W E B Magee RNCAPT P.R. Heineman USN Admiral Karl DönitzStrength 63 freighters1 destroyer2 cutters5 corvettes 18 submarines...

1984 studio album by Michael HedgesAerial BoundariesStudio album by Michael HedgesReleased1984RecordedVarious locationsGenreNew-age, worldLength37:36LabelWindham HillProducerWill Ackerman, Michael Hedges, Steven MillerMichael Hedges chronology Breakfast in the Field(1981) Aerial Boundaries(1984) Watching My Life Go By(1985) Aerial Boundaries is the second album by guitarist Michael Hedges released on the Windham Hill label in 1984. It was nominated for a Grammy Award as Best Engineere...

An academic building on the main campus of the University of Kansas 38°57′29″N 95°14′57″W / 38.95793°N 95.249265°W / 38.95793; -95.249265 The front facade of Budig Hall Budig Hall is an academic building on the main campus of the University of Kansas in Lawrence, Kansas.[1][2] The building houses one 1,000-seat lecture hall, two 500-seat lecture halls, and a computer lab.[1][2] Hoch Auditorium Hoch Auditorium was a 5,500-seat...

1983 studio album by Gladys Knight & the PipsVisionsStudio album by Gladys Knight & the PipsReleased1983Studio C. S. S. and Law Recording Studios (Las Vegas, Nevada) Studio Masters and Wally Heider Studios (Los Angeles, California) United Western Recorders, Hollywood Sound Recorders and A&M Studios (Hollywood, California) Jennifudy Studios and Larrabee Sound Studios (North Hollywood, California) Mars Recording (Santa Monica, California) Kendun Recorders (Burbank, Californi...

This article is about a high school in Potomac, Maryland. For other schools with the same (or similar) name, see Winston Churchill High School (disambiguation). Public secondary school in the United StatesWinston Churchill High SchoolAddress11300 Gainsborough Road, Potomac Maryland 20854United StatesInformationOther namesWCHS, Churchill High School, CHS, or ChurchillFormer namePotomac High SchoolTypePublic SecondaryMottoSchool of ExcellenceWhere Excellence SoarsWhere All Are Proud To BelongEs...

Fictional character Ultraman TaroUltra Series characterUltraman Taro as seen in episode 11 of Ultraman Ginga.First appearanceUltraman Taro (1973)Created byTerui SatakeDesigned byAkihiko Iguchi[1]Portrayed byHiroshi Nagasawa[2]Voiced by Japanese Saburō Shinoda (1973-74) Masako Nozawa (1984) Hiroya Ishimaru (1984-2023) Ryo Horikawa (1996) Miyu Irino (2018; stage) English William Winckler (William Winckler Productions) Bill Sullivan (2019; UGF) In-universe informationSpeciesUltr...

Soviet and Russian stage and film actor Semyon FaradaPARBornSemyon Lyvovich Ferdman(1933-12-31)December 31, 1933 Nikolskoye, Moscow Oblast, RSFSR, USSRDiedAugust 20, 2009(2009-08-20) (aged 75) Moscow, RussiaOccupationActorYears active1968—2000SpouseMaria PolitseymakoChildren1AwardsPeople's Artist of Russia (1999)Semyon Lyvovich Ferdman PAR, better known by his stage name Semyon Farada (Russian: Семён Львович Фердман, Семён Фарада, December 31, 1933, N...
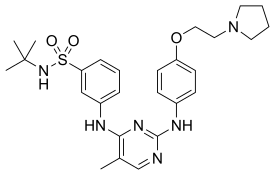
Chemical compound FedratinibClinical dataTrade namesInrebicOther namesSAR302503; TG101348AHFS/Drugs.comMonographLicense data EU EMA: by INN US DailyMed: Inrebic Routes ofadministrationBy mouthDrug classAntineoplastic agentATC codeL01EJ02 (WHO) Legal statusLegal status CA: ℞-only[1] US: ℞-only[2] EU: Rx-only[3][4] Identifiers IUPAC name N-tert-Butyl-3-{5-methyl-2-[4-(2-pyrrolidin-1-yl-ethoxy)-phenylamino]-pyrimid...


























