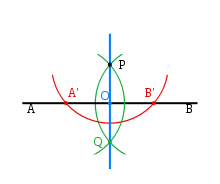
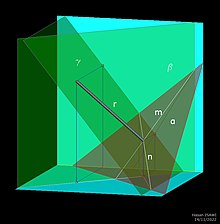
تعامد (هندسة)
|
Read other articles:

Regering-Beernaert Voorzitter van de Ministerraad Auguste Beernaert Coalitie Katholieke Partij Zetels Kamer 87 van 138 (10 juni 1884) Premier August Beernaert Aantreden 26 oktober 1884 Einddatum 26 maart 1894 Voorganger Malou Opvolger De Burlet Portaal België De regering-Beernaert (26 oktober 1884 - 26 maart 1894) was een Belgische katholieke regering. Ze volgde de regering-Malou op en werd opgevolgd door de regering-De Burlet nadat Beernaert in maart 1894 aftrad omdat z...

خريطة لمملكة إيطاليا اللومباردية والمناطق المحيطة بها حوالي عام 740 ، تُظهر جزأين رئيسيين (لانغوبارديا مايور ومينور) وتقسيماتها الداخلي. كانت دوقية تريدنتوم دوقية لومباردية مستقلة أنشأها إوين خلال فترة خلو العرش اللومباردي 574-584 التي أعقبت اغتيال ألبوين ملك اللومبارد.[1 ...

Dormelletto Gemeente in Italië Situering Regio Piëmont (PMN) Provincie Novara (NO) Coördinaten 45° 44′ NB, 8° 34′ OL Algemeen Oppervlakte 7,0 km² Inwoners (1 januari 2018) 2.600[1] (364 inw./km²) Hoogte 236 m Overig Postcode 28040 Netnummer 0322 Naam inwoner dormellettesi ISTAT-code 003062 Portaal Italië Dormelletto is een gemeente in de Italiaanse provincie Novara (regio Piëmont) en telt 2546 inwoners (31-12-2004). De oppervlakte bedraagt 7,0 km², d...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (septembre 2019). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » En pratique : Quelles sources sont attendues ? ...

WK veldrijden 1984 Datum 18-19 februari 1984 Plaats Oss, Nederland Locatie Witte Ruysheuvel Editie 35 Organisator UCI Kampioenen Mannen elite Roland Liboton Jongens junioren Ondrej Glajza Mannen amateurs Radomír Šimůnek Navigatie ← 1983 1985 → Veldrijden Portaal Wielersport WK veldrijden in Oss; Hennie Stamsnijder op kop, gevolg door latere wereldkampioen de Belg Liboton De wereldkampioenschappen veldrijden 1984 werden gehouden op 18 en 19 februari 1984 op de...

1991 Swedish filmIl Capitano: A Swedish RequiemFilm posterDirected byJan TroellWritten byPer Olov EnquistJan TroellGöran SetterbergProduced byGöran SetterbergStarringAntti ReiniMaria HeiskanenCinematographyJan TroellRelease dates 15 November 1991 (1991-11-15) (Sweden) 6 December 1991 (1991-12-06) (Finland) Running time110 minutesCountriesSwedenFinlandGermanyLanguagesFinnishSwedish Il Capitano: A Swedish Requiem (Swedish: Il Capitano) is a 1991 Swedish-F...

Species of coral Lithophyllon repanda Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Cnidaria Class: Hexacorallia Order: Scleractinia Family: Fungiidae Genus: Lithophyllon Species: L. repanda Binomial name Lithophyllon repanda(Dana, 1846)[2] Synonyms List Fungia discus Dana, 1846 Fungia integra Dana, 1846 Fungia linnaei Milne Edwards & Haime, 1851 Fungia repanda Dana, 1846 Fungia samboangensis...

String instrument LangspilLangspil in the National Museum of Iceland, in Reykjavik, Iceland.String instrumentClassification String instruments Hornbostel–Sachs classification314.1(true board zither)Related instruments Langeleik, Scheitholt, Epinette des Vosges, Dulcimer The langspil (Icelandic pronunciation: [ˈlauŋkˌspɪːl̥]; meaning long-play) is a traditional Icelandic drone zither. It has a single melody string and usually 2 drone strings. The langspil can be played by pluck...

1959 film by Jampana Minnal VeeranTheatrical release posterDirected byJampanaStory byA. L. NarayananProduced byR. KalyanaramanStarringRanjanSandhyaCinematographyS. J. ThomasW. R. Subba RaoMusic byVedhaProductioncompanyT. N. R. ProductionsRelease date 20 March 1959 (1959-03-20) CountryIndiaLanguageTamil Minnal Veeran (transl. Lightning Warrior) is a 1959 Indian Tamil-language action adventure film directed by Jampana. The film stars Ranjan and Sandhya. It was released on 2...

Ancient Greek Stoic philosopher For the Epicurean philosopher, also from Seleucia, see Diogenes of Seleucia. Diogenes of Babylon (also known as Diogenes of Seleucia; Greek: Διογένης Βαβυλώνιος; Latin: Diogenes Babylonius; c. 230 – c. 150/140 BC[1]) was a Stoic philosopher. He was the head of the Stoic school in Athens, and he was one of three philosophers sent to Rome in 155 BC. He wrote many works, but none of his writings survived, except as quotations by later w...

У Вікіпедії є статті про інші географічні об’єкти з назвою Веслі-Чапел. Переписна місцевість Веслі-Чапелангл. Wesley Chapel Координати 28°10′42″ пн. ш. 82°21′02″ зх. д. / 28.17860000002777809° пн. ш. 82.350600000027782244° зх. д. / 28.17860000002777809; -82.350600000027782244Координати: 28°10�...

Academy in Coulsdon, London, EnglandWoodcote High SchoolAddressMeadow RiseCoulsdon, London, CR5 2EHEnglandCoordinates51°19′51″N 0°08′29″W / 51.330803°N 0.141304°W / 51.330803; -0.141304InformationTypeAcademyEstablished5 July 1957Local authorityLondon Borough of CroydonSpecialistSports College, Mathematics and Computing CollegeDepartment for Education URN138187 TablesOfstedReportsGenderCoeducationalAge11 to 18HousesMooreThompsonRedgraveHolmesWebsitehttps...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2021) نادية هناوي معلومات شخصية اسم الولادة نادية هناوي مواطنة عراقيّة الجنسية العراق العرق عرب الحياة العملية الفترة 2005 – حاليًا النوع روايات كتب المواضيع م�...

California county routes in zone E This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: California county routes in zone E – news · newspapers · books · scholar · JSTOR (January 2010) (Learn how and when to remove this template message) California county routes in zone EExample of a California county route shield...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Don Mills Centre – news · newspapers · books · scholar · JSTOR (May 2014) (Learn how and when to remove this template message) The centre during demolition in 2006 The Don Mills Centre was a shopping mall in Toronto, Ontario, Canada. It was located on a 44-acre...

For the women's race, see 2023 Strade Bianche Donne. Cycling race 2023 Strade Bianche2023 UCI World Tour, race 5 of 35Race detailsDates4 March 2023Stages1Distance184 km (114.3 mi)Winning time4h 31' 41Results Winner Tom Pidcock (GBR) (Ineos Grenadiers) Second Valentin Madouas (FRA) (Groupama–FDJ) Third Tiesj Benoot (BEL) (Team Jumbo–Visma)← 2022 2024 → The 17th edition of Strade Bianche was held on 4 March 2...

Grabdenkmäler Die Filialkirche St. Johann in der Gemeinde Wolfsberg steht unter dem Patrozinium Johannes der Täufer und gehört zur Pfarre St. Markus. St. Johann wurde schon sehr früh von der Mutterpfarre St. Marein im ausgehenden 11. oder zu Anfang des 12. Jahrhunderts gegründet und noch vor 1218 zur eigenständigen Pfarre erhoben. Letztmals wird St. Johann 1784 als Pfarre genannt. Inhaltsverzeichnis 1 Baubeschreibung 2 Einrichtung 3 Literatur 4 Weblinks Baubeschreibung Vom romanischen B...

Leonard Woolley, arkeolog yang pertama kali melakukan penggalian di Alalakh Alalakh adalah salah satu daerah di Siria Utara.[1] Letaknya sangat dekat dengan sungai Orentes.[2] Daerah ini dikenal sebagai salah satu sumber benda-benda purbakala.[1] Penggalian benda-benda purbakala di daerah ini pertama kali dilakukan oleh Leonard Woolley, seorang ahli bidang arkeologi asal Inggris.[1] Dia melakukan penggalian dalam dua periode, yaitu tahun 1937 hingga 1939 dan ta...

Project A Part IIHong Kong film posterNama lainTradisionalA計劃續集SederhanaA计划续集MandarinA Jìhuà XùjíKantonA Gai3 Waak6 Zuk6 Zaap6 Sutradara Jackie Chan Produser Raymond Chow Leonard Ho David Lam (film director) Edward Tang Ditulis oleh Jackie Chan Edward Tang PemeranJackie ChanMaggie CheungRosamund KwanBill TungPenata musikMichael LaiSinematograferCheung Yiu-tsouPenyuntingPeter Cheung Yiu-chungDistributorGolden HarvestMedia AsiaTanggal rilis 19 Agustus 1987 (...

Cycling race 2022 Tour of Britain2022 UCI ProSeriesStage 5 in RetfordRace detailsDates4 – 8 September 2022Stages5Results Winner Gonzalo Serrano (ESP) (Movistar Team) Second Tom Pidcock (GBR) (Ineos Grenadiers) Third Omar Fraile (ESP) (Ineos Grenadiers) Points Tom Pidcock (GBR) (Ineos Grenadiers) Mountains Mathijs Paasschens (NED) (Bingoal Pauwels Sauces WB) Sprints Matthew Teggart (IRL) (WiV SunGod) Team Ine...