žŻ┘å┘łž¦ž╣ ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž®:┘éžĘž╣ ┘ģ┘āž¦┘üž” ž»ž¦ž”ž▒ž® ┘ł┘éžĘž╣ ┘垦┘鞥 ┘éžĘž╣ ž▓ž¦ž”ž» ┘ü┘Ŗ ž¦┘äž▒┘Ŗž¦žČ┘Ŗž¦ž¬ ┘łž©ž¦┘䞬žŁž»┘Ŗž» ┘ü┘Ŗ ž¦┘ä┘ć┘åž»ž│ž® ž¦┘ä┘łžĄ┘ü┘Ŗž® žī ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ┘ć┘ł ┘ģ┘åžŁ┘å┘ē ┘垦ž¬ž¼ ž╣┘å ž¬┘鞦žĘž╣ ┘ģž«ž▒┘łžĘ
K
{\displaystyle K}
┘ģž│ž¬┘ł ┘䞦 ┘Ŗ┘ģž▒ ž©ž▒žŻž│
K
{\displaystyle K}
ž»┘Åž▒ž│ž¬ ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® ┘ģ┘åž░ ┘ł┘鞬 žĘ┘ł┘Ŗ┘ä ┘Ŗž╣┘łž» žź┘ä┘ē 200 ┘éž©┘ä ž¦┘ä┘ģ┘Ŗ┘䞦ž» ž╣┘åž»┘ģž¦ ┘鞦┘ģ žŻž©┘ä┘ł┘å┘Ŗ┘łž│ ž¦┘äž©ž▒ž║ž¦┘ł┘Ŗ ž©žźž¼ž▒ž¦žĪ ž»ž▒ž¦ž│ž® ž¬ž©┘Ŗ┘å ž«žĄž¦ž”žĄ┘枦.
┘ü┘Ŗ ž¦┘䞬žŁ┘ä┘Ŗ┘ä ž¦┘äž▒┘Ŗž¦žČ┘Ŗ ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ┘ć┘ł ž¦┘ä┘ģžŁ┘ä ž¦┘ä┘ć┘åž»ž│┘Ŗ ┘ä┘å┘éžĘž® ž¬ž¬žŁž▒┘ā ž©žŁ┘Ŗž½ ž¬┘ā┘ł┘å ž¦┘äž╣┘䞦┘éž®┘Å ž©┘Ŗ┘å┘Ä ž©ž╣ž»┘枦 ž╣┘å ┘å┘éžĘž®┘Ź ž½ž¦ž©ž¬ž®┘Ź ┘łž©ž╣ž»┘枦 ž╣┘å ┘ģž│ž¬┘é┘Ŗ┘ģ┘Ź ž½ž¦ž©ž¬┘Ź ┘åž│ž©ž®┘ŗ ž½ž¦ž©ž¬ž®┘ŗ.
ž¬ž│┘ģ┘ē ┘ćž░┘ć ž¦┘ä┘åž│ž©ž® ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ (Eccentricity)žī ┘ā┘ģž¦ ž¬ž│┘ģ┘ē ž¦┘ä┘å┘éžĘž® ž¦┘äž½ž¦ž©ž¬ž® ž¦┘äž©žżž▒ž® (Focus)žī žŻ┘ģž¦ ž¦┘ä┘ģž│ž¬┘é┘Ŗ┘ģ ž¦┘äž½ž¦ž©ž¬ ┘ü┘Ŗž│┘ģ┘ē ž¦┘äž»┘ä┘Ŗ┘ä (directrix).
P
S
=
e
.
P
M
{\displaystyle PS=e.PM}
žŁ┘Ŗž½:
- P ┘ć┘Ŗ ┘å┘éžĘž® (x,y) ž¬┘éž╣ ž╣┘ä┘ē ž¦┘ä┘éžĘž╣.
- S ž¦┘äž©žżž▒ž®
- e ┘ģž╣ž¦┘ģ┘ä ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ
- ┘ł m ┘ć┘Ŗ ┘ģž│┘éžĘ ž¦┘äž╣┘ģ┘łž»┘Ŗ ┘ä P ž╣┘ä┘ē ž¦┘äž»┘ä┘Ŗ┘ä.
žźž░ž¦ ┘āž¦┘å ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ ┘ģž│ž¦┘ł┘Ŗž¦ ┘ä┘ä┘łžŁž»ž® (┘Ŗž│ž¦┘ł┘Ŗ ž¦┘ä┘łž¦žŁž») ž│┘Å┘ģ┘É┘æ┘Ŗ┘Ä ž¦┘ä┘ģ┘åžŁ┘å┘ē ┘éžĘž╣┘ŗž¦ ┘ģ┘āž¦┘üž”┘ŗž¦ (Parabola)žī ┘łžźž░ž¦ ┘āž¦┘å ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ žŻ┘é┘ä ┘ģ┘å ž¦┘ä┘łžŁž»ž® ž│┘ģ┘Ŗ ž¦┘ä┘ģ┘åžŁ┘å┘ē ┘éžĘž╣ž¦ ┘垦┘鞥ž¦ (Ellipse)žī ┘łžźž░ž¦ ┘āž¦┘å ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ žŻ┘āž©ž▒ ┘ģ┘å ž¦┘ä┘łžŁž»ž® ž│┘ģ┘Ŗ ž¦┘ä┘ģ┘åžŁ┘å┘ē ┘éžĘž╣ž¦ ž▓ž¦ž”ž»ž¦ (Hyperbola).
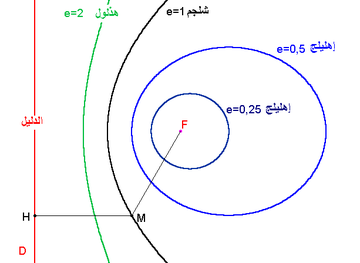
┘łž¬ž│┘ģ┘ē ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģ┘āž¦┘üž”ž® ┘łž¦┘ä┘垦┘鞥ž® ┘łž¦┘äž▓ž¦ž”ž»ž® ž©ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® žī ┘䞯┘å┘ć ┘Ŗ┘ģ┘ā┘å žŻ┘å ž¬ž¬┘ł┘äž» ┘垬┘Ŗž¼ž® ┘éžĘž╣ ž¦┘äž│žĘžŁ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ž©┘ģž│ž¬┘ł ┘ü┘Ŗ ┘łžČž╣ ┘ģž╣┘Ŗ┘å.
┘ä┘枦 ž½┘䞦ž½ž® žŻ┘å┘łž¦ž╣ ┘ć┘Ŗ ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģ┘āž¦┘üž” (ž┤┘äž¼┘ģ)žī ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž» (┘ćž░┘ä┘ł┘ä)žī ┘łž¦┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥 (žź┘ć┘ä┘Ŗ┘äž¼). ┘ł┘éž» ž¬┘Åž╣ž»┘Å┘æ ž¦┘äž»ž¦ž”ž▒ž® ┘å┘łž╣┘ŗž¦ ž▒ž¦ž©ž╣┘ŗž¦ (┘ā┘ģž¦ ž╣ž»┘Ä┘æ┘枦 žŻž©┘ł┘ä┘ł┘å┘Ŗ┘łž│ ) žŻ┘ł ┘Ŗ┘ģ┘ā┘å ž╣ž»┘Å┘æ┘枦 ┘å┘łž╣ž¦ ┘ģ┘å ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘垦┘鞥ž® (ž╣┘åž»┘ģž¦ ┘Ŗ┘ā┘ł┘å ž¦┘ä┘ģžŁ┘łž▒ž¦┘å ┘ģž¬ž│ž¦┘ł┘Ŗž¦┘å). ┘ł┘Ŗž¬ž┤┘ā┘ä ž¦┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥 ┘łž¦┘äž»ž¦ž”ž▒ž® ž╣┘åž»┘ģž¦ ┘Ŗ┘ā┘ł┘å ž¬┘鞦žĘž╣ ž¦┘ä┘ģž│ž¬┘ł┘ē ┘łž¦┘ä┘ģž«ž▒┘łžĘ ┘ģ┘åžŁ┘å┘ē ┘ģž║┘ä┘é. ┘łž¬ž¬ž┤┘ā┘ä ž¦┘äž»ž¦ž”ž▒ž® ž╣┘åž»┘ģž¦ ┘Ŗ┘ā┘ł┘å ž¦┘ä┘ģž│ž¬┘ł┘ē ž¦┘ä┘鞦žĘž╣ ┘ģ┘łž¦ž▓┘Ŗ┘ŗž¦ ┘äž»ž¦ž”ž▒ž® ž¦┘ä┘鞦ž╣ž»ž® ž¦┘ä┘ģ┘ł┘äž»ž® ┘ä┘ä┘ģž«ž▒┘łžĘ (┘ł┘ü┘Ŗ ┘ćž░┘ć ž¦┘䞣ž¦┘äž® ┘Ŗž│┘ģ┘ē ┘ģž«ž▒┘łžĘ ž»ž¦ž”ž▒┘Ŗ ). ž©ž¦┘ä┘åž│ž©ž® ┘ä┘ģž«ž▒┘łžĘ ┘Ŗ┘ģ┘Ŗ┘å┘Ŗ (┘ā┘ģž¦ ┘ü┘Ŗ ž¦┘äž┤┘ā┘ä ž¦┘ä┘ģ┘鞦ž©┘ä ┘ü┘Ŗ žŻž╣┘ä┘ē ž¦┘䞥┘łž▒ž®) ┘Ŗ┘ā┘ł┘å ž¦┘ä┘ģž│ž¬┘ł┘ē ž¦┘ä┘鞦žĘž╣ ž╣┘ģ┘łž»┘Ŗ┘ŗž¦ ž╣┘ä┘ē ┘ģžŁ┘łž▒ ž¬┘ģž¦ž½┘ä ž¦┘ä┘ģž«ž▒┘łžĘ. žźž░ž¦ ┘āž¦┘å ž¦┘ä┘ģž│ž¬┘ł┘ē ž¦┘ä┘鞦žĘž╣ ┘ģ┘łž¦ž▓┘Ŗž¦ ┘äž«žĘ ┘łž¦žŁž» ┘ü┘éžĘ ┘ģ┘å ž¦┘äž«žĘ┘łžĘ ž¦┘ä┘ģ┘ł┘äž»ž® ┘ä┘ä┘ģž«ž▒┘łžĘ žŁ┘Ŗ┘å┘枦 ┘ŖžĄž©žŁ ž¦┘ä┘éžĘž╣ ┘ģ┘üž¬┘łžŁ┘ŗž¦ ┘ł┘ä┘Ŗž│ ┘ģž║┘ä┘é┘ŗž¦ ┘ü┘Ŗž│┘ģ┘ē ┘éžĘž╣┘ŗž¦ ┘ģ┘āž¦┘üž”┘ŗž¦ . ┘ł┘ü┘Ŗ ž¦┘䞣ž¦┘äž® ž¦┘䞯ž«┘Ŗž▒ž® ┘Ŗž¬┘ā┘ł┘å ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž» ┘łž╣┘åž»┘ģž¦ ┘Ŗ┘ā┘ł┘å ž¦┘ä┘ģž│ž¬┘ł┘ē ┘ģ┘łž¦ž▓┘Ŗ ┘äž▒ž¦ž│┘ģ┘Ŗ┘å ┘ģ┘å ž▒┘łž¦ž│┘ģ ž¦┘ä┘ģž«ž▒┘łžĘ ┘łž©ž¦┘䞬ž¦┘ä┘Ŗ ┘Ŗ┘éžĘž╣ ┘ā┘䞦 ž¦┘äžĘ┘Ŗž¬┘Ŗ┘å žī ┘ģ┘ā┘ł┘å┘ŗž¦ ž©ž░┘ä┘ā ┘ģ┘åžŁ┘å┘Ŗ┘Ŗ┘å ┘ģ┘å┘üžĄ┘ä┘Ŗ┘å ┘ł┘ģ┘üž¬┘łžŁ┘Ŗ┘åžī ┘Ŗž¬┘ģ žŻžŁ┘Ŗž¦┘垦 ž¬ž¼ž¦┘ć┘ä žŻžŁž»┘ć┘ģž¦ ┘łž¦┘äž╣┘ģ┘ä ž©ž¦┘äžóž«ž▒.
ž¬┘łž¼ž» žŁž¦┘䞦ž¬ ž┤ž¦ž░ž® ž¬┘垬ž¼ ž╣┘åž»┘ģž¦ ┘Ŗ┘ģž▒ ž¦┘ä┘ģž│ž¬┘ł┘ē ž¦┘ä┘鞦žĘž╣ ž©ž▒žŻž│ ž¦┘ä┘ģž«ž▒┘łžĘ Apex. ž¦┘䞬┘鞦žĘž╣ ┘ü┘Ŗ ┘ćž░┘ć ž¦┘䞣ž¦┘䞦ž¬ ┘éž» ┘Ŗ┘ā┘ł┘å ž«žĘ┘ŗž¦ ┘ģž│ž¬┘é┘Ŗ┘ģž¦ (žźž░ž¦ ┘āž¦┘å ž¦┘ä┘ģž│ž¬┘ł┘ē ┘ģ┘ģž¦ž│┘ŗž¦ ┘äž│žĘžŁ ž¦┘ä┘ģž«ž▒┘łžĘ)žø žŻ┘ł ┘å┘éžĘž® (žźž░ž¦ ┘āž¦┘垬 ž¦┘äž▓ž¦┘ł┘Ŗž® ž©┘Ŗ┘å ž¦┘ä┘ģž│ž¬┘ł┘ē ┘ł┘ģžŁ┘łž▒ ž¦┘ä┘ģž«ž▒┘łžĘ žŻ┘āž©ž▒ ┘ģ┘å ž¦┘ä┘ģ┘ģž¦ž│)žø žŻ┘ł ž▓┘łž¼ž¦ ┘ģ┘å ž¦┘äž«žĘ┘łžĘ ž¦┘ä┘ģž¬┘鞦žĘž╣ž® (ž╣┘åž»┘ģž¦ ž¬┘ā┘ł┘å ž¦┘äž▓ž¦┘ł┘Ŗž® žŻžĄž║ž▒).
ž╣┘åž»┘ģž¦ ┘ŖžĄž©žŁ ž¦┘ä┘ģž«ž▒┘łžĘ žŻž│žĘ┘łž¦┘åž® žŻ┘Ŗ ž╣┘åž»┘ģž¦ ┘Ŗ┘ā┘ł┘å ž¦┘äž▒žŻž│ ┘łž¦┘éž╣ž¦ ┘ü┘Ŗ ┘ģ┘åžĘ┘éž® ž¦┘ä┘䞦┘å┘枦┘Ŗž® ž¬┘垬ž¼ ┘éžĘ┘łž╣ žŻž│žĘ┘łž¦┘å┘Ŗž® . ž©ž¦┘äž▒ž║┘ģ ┘ģ┘å žŻ┘å ž░┘ä┘ā ┘Ŗž¬ž│ž©ž© ž║ž¦┘äž©┘ŗž¦ ┘ü┘Ŗ ┘éžĘž╣ ┘垦┘鞥 žŻ┘ł ž»ž¦ž”ž▒ž®žī žź┘䞦 žŻ┘å ┘ć┘垦┘ā žŁž¦┘äž® ž┤ž¦ž░ž® ž¬┘垬ž¼ ž«žĘ žŻ┘ł ž«žĘ┘Ŗ┘å ┘ģž¬┘łž¦ž▓┘Ŗ┘Ŗ┘å ž╣┘åž»┘ģž¦ ┘Ŗ┘ā┘ł┘å ┘ģž│ž¬┘ł┘ē ž¦┘ä┘éžĘž╣žī ž©ž¦┘䞬┘łž¦┘ä┘Ŗžī ┘ģž¬┘ģž¦ž│ ┘ä┘䞯ž│žĘ┘łž¦┘åž® žŻ┘ł ┘鞦žĘž╣ž¦ ┘ä┘枦 (ž©ž┤ž▒žĘ žŻ┘å ┘Ŗ┘ā┘ł┘å ┘ģ┘łž¦ž▓┘Ŗ ┘äž▒ž¦ž│┘ģ ┘ģ┘å ž▒┘łž¦ž│┘ģ┘枦 )
ž¦┘åžĖž▒ žŻ┘ŖžČž¦┘ŗ: ┘䞦 ┘ģž▒┘āž▓┘Ŗž® (ž▒┘Ŗž¦žČ┘Ŗž¦ž¬) ž┤ž▒┘łžĘ ž¦┘䞬ž╣ž▒┘Ŗ┘ü ž¦┘䞯ž▒ž©ž╣ž® ž¦┘ä┘łž¦ž▒ž»ž® žŻž╣┘䞦┘ć ┘Ŗ┘ģ┘ā┘å ž¼┘ģž╣┘枦 ┘ü┘Ŗ ž┤ž▒žĘ ┘łž¦žŁž» ┘Ŗž╣ž¬┘ģž» ž╣┘ä┘ē ┘å┘éžĘž® ž¦┘üž¬ž▒ž¦žČ┘Ŗž® F (ž¦┘äž©žżž▒ž®) ┘ł┘ģž│ž¬┘é┘Ŗ┘ģ L (ž¦┘äž»┘ä┘Ŗ┘ä) ┘䞦 ┘Ŗ┘ģž▒ ž©ž¦┘ä┘å┘éžĘž® F ┘łž╣ž»ž» žŁ┘é┘Ŗ┘é┘Ŗ ž║┘Ŗž▒ ž│ž¦┘äž© e (┘ć┘ł ┘ģž╣ž¦┘ģ┘ä ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ). ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ž¦┘ä┘ģ┘鞦ž©┘ä ┘Ŗž¬┘ā┘ł┘å ┘ģ┘å ž¼┘ģ┘Ŗž╣ ž¦┘ä┘å┘鞦žĘ ž¦┘䞬┘Ŗ ž¬ž©ž╣ž» ž╣┘å F ┘ģž│ž¦┘üž®┘ŗ ž¬ž│ž¦┘ł┘Ŗ e ┘ģž▒ž® ž©ž╣ž»┘枦 ž╣┘å L . žźž░ž¦ ┘āž¦┘垬 e ž©┘Ŗ┘å 0 ┘ł 1 ┘åžŁžĄ┘ä ž╣┘ä┘ē ┘éžĘž╣ ┘垦┘鞥žī žźž░ž¦ ┘āž¦┘垬 e =1 ┘垬žŁžĄ┘ä ž╣┘ä┘ē ┘éžĘž╣ ┘ģ┘āž¦┘üž” ┘łžźž░ž¦ ┘āž¦┘垬 žŻ┘āž©ž▒ ┘ģ┘å 1 ┘åžŁžĄ┘ä ž╣┘ä┘ē ┘éžĘž╣ ž▓ž¦ž”ž».
┘Ŗ┘łž¼ž» ž»┘ä┘Ŗ┘䞦┘å ┘łž©žżž▒ž¬ž¦┘å ┘ä┘ā┘ä ┘ģ┘å ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž» ┘łž¦┘ä┘垦┘鞥. ž¦┘ä┘ģž│ž¦┘üž® ┘ģ┘å ž¦┘ä┘ģž▒┘āž▓ žź┘ä┘ē ž¦┘äž»┘ä┘Ŗ┘ä ┘ć┘Ŗ
a
/
e
{\displaystyle a/e}
a
{\displaystyle a\ }
┘åžĄ┘ü ž¦┘ä┘ģžŁ┘łž▒ ž¦┘䞯┘āž©ž▒ ┘ä┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥žī žŻ┘ł ž¦┘ä┘ģž│ž¦┘üž® ┘ģ┘å ž¦┘ä┘ģž▒┘āž▓ žź┘ä┘ē ┘é┘ģž® ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž». ž¦┘ä┘ģž│ž¦┘üž® ┘ģ┘å ž¦┘ä┘ģž▒┘āž▓ ┘ä┘äž©žżž▒ž® ┘ć┘Ŗ
a
e
{\displaystyle ae\ }
┘ü┘Ŗ žŁž¦┘äž® ž¦┘äž»ž¦ž”ž▒ž® ┘Ŗ┘ā┘ł┘å ┘ģž╣ž¦┘ģ┘ä ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ e = 0 ┘ł┘Ŗ┘ģ┘ā┘å ž¬ž«┘Ŗ┘ä žŻ┘å ž¦┘äž»┘ä┘Ŗ┘ä ┘éž» ž¦┘Åž│┘Æž¬┘Åž©┘Æž╣┘Éž» ┘䞦┘å┘枦ž”┘Ŗ┘ŗž¦ ž╣┘å ž¦┘ä┘ģž▒┘āž▓. ┘ä┘ā┘å ┘ģ┘å ž║┘Ŗž▒ ž¦┘ä┘ģ┘ü┘Ŗž» ž¦ž│ž¬ž«ž»ž¦┘ģ ž¦┘䞬ž╣ž©┘Ŗž▒: žź┘å ž¦┘äž»ž¦ž”ž▒ž® ž¬ž¬┘ā┘ł┘å ┘ģ┘å ┘ā┘ä ž¦┘ä┘å┘鞦žĘ ž¦┘䞬┘Ŗ ž¦┘䞬┘Ŗ ž¬ž©ž╣ž» ┘ģž│ž¦┘üž® e ┘ģž▒ž® ž©ž╣ž»┘枦 ž╣┘å L ┘䞯┘å┘垦 ž│┘åžŁžĄ┘ä ž╣┘ä┘ē 0 ┘ģžČž▒┘łž©ž® ┘ü┘Ŗ ┘ģž¦┘䞦┘å┘枦┘Ŗž®.
┘äž░┘ä┘ā ┘üžź┘å ž¦┘ä┘ģ┘ģ┘Ŗž▓ ž¦┘䞯ž│ž¦ž│┘Ŗ ┘ģž¦ ┘Ŗž«žĄ ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ┘ć┘ł ┘ģ┘é┘Ŗž¦ž│ ┘Ŗž©┘Ŗ┘å ┘䞯┘Ŗ ┘ģž»┘ē ┘Ŗž©ž╣ž» ž¦┘ä┘éžĘž╣ ž╣┘å žŻ┘å ┘Ŗ┘ā┘ł┘å ž»ž¦ž”ž▒ž®. ┘ä┘é┘Ŗ┘ģž® ┘ģž╣žĘž¦ž®
a
{\displaystyle a\ }
e
{\displaystyle e\ }
┘åžĄ┘ü ž¦┘ä┘ģžŁ┘łž▒ ┘łž¦┘䞯žĄž║ž▒ .
┘ģžŁž»ž»ž¦ž¬ ž¦┘ä┘éžĘž╣ ┘ü┘Ŗ žŁž¦┘äž® ž¦┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥 ž©ž¦┘äžźžČž¦┘üž® žź┘ä┘ē ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ (e)žī ┘łž¦┘äž©žżž▒žī ┘łž¦┘äž»┘ä┘Ŗ┘äžī ž¬ž▒ž¬ž©žĘ ž¦┘äž╣ž»┘Ŗž» ┘ģ┘å ž¦┘ä┘ģ┘Ŗž▓ž¦ž¬ ┘łž¦┘䞯žĘ┘łž¦┘ä ž¦┘ä┘ć┘åž»ž│┘Ŗž® ž©┘éžĘž╣ ┘ģž«ž▒┘łžĘ┘Ŗ.
ž¦┘ä┘ģžŁ┘łž▒ ž¦┘äž▒ž”┘Ŗž│┘Ŗ : ┘ć┘ł ž¦┘ä┘ģž│ž¬┘é┘Ŗ┘ģ ž¦┘äž░┘Ŗ ┘Ŗž┤┘ģ┘ä ž©žżž▒ ž¦┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥 žŻ┘ł ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž»žī ┘ł┘ģž▒┘āž▓┘枦 ┘ć┘Ŗ ┘ģž▒┘āž▓ ž¦┘ä┘ģ┘åžŁ┘å┘ē. ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģ┘āž¦┘üž” ┘ä┘Ŗž│ ┘ä┘ć ┘ģž▒┘āž▓.
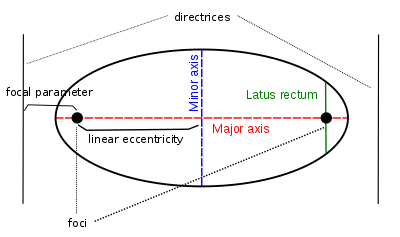
ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ ž¦┘äž«žĘ┘Ŗ c (ž©ž¦┘äžź┘åž¼┘ä┘Ŗž▓┘Ŗž® : Linear eccentricity )ŌĆÅ ┘ć┘Ŗ ž¦┘ä┘ģž│ž¦┘üž® ž©┘Ŗ┘å ž¦┘ä┘ģž▒┘āž▓ ┘łž¦┘äž©žżž▒ž®.
ž¦┘ä┘łž¬ž▒ ž¦┘äž╣┘ģ┘łž»┘Ŗ ž¦┘äž©žżž▒┘Ŗ (ž©ž¦┘ä┘䞦ž¬┘Ŗ┘å┘Ŗž® : latus rectum ) ž¦┘ä┘łž¬ž▒ ž¦┘ä┘ģ┘łž¦ž▓┘Ŗ ┘ä┘äž»┘ä┘Ŗ┘ä ┘ł┘Ŗ┘ģž▒ ž╣ž©ž▒ ž¦┘äž©žżž▒ž®žø ┘åžĄ┘ü žĘ┘ł┘ä┘ć ┘ć┘ł ┘åžĄ┘ü ž¦┘ä┘łž¬ž▒ ž¦┘äž╣┘ģ┘łž»┘Ŗ ž¦┘äž©žżž▒┘Ŗ (Ōäō).
ž¦┘ä┘ģžŁž»ž» ž¦┘äž©žżž▒┘Ŗ p (ž©ž¦┘äžź┘åž¼┘ä┘Ŗž▓┘Ŗž® : Focal parameter )ŌĆÅ ┘ć┘ł ž¦┘ä┘ģž│ž¦┘üž® ž©┘Ŗ┘å ž¦┘äž©žżž▒ž® ž¦┘ä┘ģ┘鞦ž©┘äž®.
ž¦┘ä┘ģžŁ┘łž▒ ž¦┘䞯┘āž©ž▒ (ž©ž¦┘äžź┘åž¼┘ä┘Ŗž▓┘Ŗž® : Major axis )ŌĆÅ ┘ć┘ł ž¦┘ä┘łž¬ž▒ ž©┘Ŗ┘å ž¦┘äž▒žŻž│┘Ŗ┘å: žŻžĘ┘ł┘ä ┘łž¬ž▒ ┘ä┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥žī ┘łžŻ┘鞥ž▒ ┘łž¬ž▒ ž©┘Ŗ┘å ┘üž▒ž╣┘Ä┘Ŗ┘Æ ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž»žī ┘ŖžĘ┘ä┘é ž╣┘ä┘ē ┘åžĄ┘ü žĘ┘ł┘ä┘ć ž¦ž│┘ģ ┘åžĄ┘ü ž¦┘ä┘ģžŁ┘łž▒ ž¦┘䞯┘āž©ž▒ a
ž¦┘ä┘ģžŁ┘łž▒ ž¦┘䞯žĄž║ž▒ (ž©ž¦┘äžź┘åž¼┘ä┘Ŗž▓┘Ŗž® : Minor axis )ŌĆÅ ┘ć┘ł žŻ┘鞥ž▒ ┘éžĘž▒ ┘ä┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥žī ┘ł┘åžĄ┘ü žĘ┘ł┘ä┘ć ┘ŖžĘ┘ä┘é ž╣┘ä┘Ŗ┘ć ┘åžĄ┘ü ž¦┘ä┘ģžŁ┘łž▒ ž¦┘䞯žĄž║ž▒ bžī ┘å┘üž│ ž¦┘ä┘é┘Ŗ┘ģž® b ┘ā┘ģž¦ ┘ü┘Ŗ ž¦┘ä┘ģž╣ž¦ž»┘äž® ž¦┘ä┘é┘Ŗž¦ž│┘Ŗž® žŻž»┘垦┘ć. ž╣┘ä┘ē ž│ž©┘Ŗ┘ä ž¦┘ä┘é┘Ŗž¦ž│žī ž©ž¦┘ä┘åž│ž©ž® ┘ä┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž»žī ┘åž│┘ģ┘Ŗ žŻ┘ŖžČ┘ŗž¦ ž¦┘ä┘ģž╣┘ä┘ģž® b ┘ü┘Ŗ ž¦┘ä┘ģž╣ž¦ž»┘äž® ž¦┘ä┘é┘Ŗž¦ž│┘Ŗž®žī ž┤ž©┘ć ž¦┘ä┘ģžŁ┘łž▒ ž¦┘䞯žĄž║ž▒.
┘ü┘Ŗ┘ģž¦ ┘Ŗ┘ä┘Ŗ ž╣┘䞦┘éž® ž©ž╣žČ ž¦┘ä┘ģžŁž»ž»ž¦ž¬ ž¦┘ä┘ģž░┘ā┘łž▒ž® žŻž╣┘䞦┘ć ž©ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ:[ 1]
ℓ Ōäō -->
=
p
e
{\displaystyle \ \ell =pe}
c
=
a
e
{\displaystyle \ c=ae}
p
+
c
=
a
e
{\displaystyle \ p+c={\frac {a}{e}}}
ž©ž¦┘ä┘åž│ž©ž® ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® ┘ü┘Ŗ ž¦┘ä┘łžČž╣ ž¦┘ä┘é┘Ŗž¦ž│┘Ŗžī ┘üžź┘å ┘ćž░┘ć ž¦┘ä┘ģžŁž»ž»ž¦ž¬ ┘ä┘枦 ž¦┘ä┘é┘Ŗ┘ģ ž¦┘䞬ž¦┘ä┘Ŗž®žī ┘ģž╣ žŻž«ž░
a
,
b
>
0
{\displaystyle a,b>0}
┘éžĘž╣ ┘ģž«ž▒┘łžĘ┘Ŗ
┘ģž╣ž¦ž»┘äž®
ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ (e
ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ ž¦┘äž«žĘ┘Ŗ (c
┘åžĄ┘ü ž¦┘ä┘łž¬ž▒ ž¦┘äž╣┘ģ┘łž»┘Ŗ ž¦┘äž©žżž▒┘Ŗ (Ōäō
┘ģžŁž»ž» ž©žżž▒┘Ŗ (p
ž»ž¦ž”ž▒ž®
x
2
+
y
2
=
a
2
{\displaystyle x^{2}+y^{2}=a^{2}\,}
0
{\displaystyle 0\,}
0
{\displaystyle 0\,}
a
{\displaystyle a\,}
∞ Ōł× -->
{\displaystyle \infty }
┘éžĘž╣ ┘垦┘鞥
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}
1
− ŌłÆ -->
b
2
a
2
{\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}
a
2
− ŌłÆ -->
b
2
{\displaystyle {\sqrt {a^{2}-b^{2}}}}
b
2
a
{\displaystyle {\frac {b^{2}}{a}}}
b
2
a
2
− ŌłÆ -->
b
2
{\displaystyle {\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}}
┘éžĘž╣ ┘ģ┘āž¦┘üž”
y
2
=
4
a
x
{\displaystyle y^{2}=4ax\,}
1
{\displaystyle 1\,}
ž║┘Ŗž▒ ┘ģ┘łž¼┘łž»
2
a
{\displaystyle 2a\,}
2
a
{\displaystyle 2a\,}
┘éžĘž╣ ž▓ž¦ž”ž»
x
2
a
2
− ŌłÆ -->
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}
1
+
b
2
a
2
{\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}
a
2
+
b
2
{\displaystyle {\sqrt {a^{2}+b^{2}}}}
b
2
a
{\displaystyle {\frac {b^{2}}{a}}}
b
2
a
2
+
b
2
{\displaystyle {\frac {b^{2}}{\sqrt {a^{2}+b^{2}}}}}
┘Ŗ┘ģ┘ā┘å ž¬┘ģž½┘Ŗ┘ä ┘ģž╣ž¦ž»┘äž® ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ž©žŻž┤┘āž¦┘ä ┘ģž«ž¬┘ä┘üž® ┘ģ┘å┘枦:
žźž░ž¦ ┘āž¦┘å ž¦┘䞦ž«ž¬┘䞦┘ü ž¦┘ä┘ģž▒┘āž▓┘Ŗ ┘Ŗž│ž¦┘ł┘Ŗ ┌Š ┘ł┘āž¦┘垬 ž¦┘äž©žżž▒ž® ž╣┘åž» ┘å┘éžĘž® ž¦┘䞯žĄ┘ä (0,0) ┘łž¦┘äž»┘ä┘Ŗ┘ä ┘ģž│ž¬┘é┘Ŗ┘ģž¦ ž╣┘ģ┘łž»┘Ŗž¦ ž╣┘ä┘ē ┘ģžŁ┘łž▒ ž¦┘äž│┘Ŗ┘垦ž¬ ┘Ŗ┘éžĘž╣┘ć ž╣┘ä┘ē ž©ž╣ž» ┘ü ┘üžź┘å ┘ģž╣ž¦ž»┘äž® ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ž¬ž╣žĘ┘ē ž©ž¦┘ä┘ģž╣ž¦ž»┘äž® ž¦┘䞬ž¦┘ä┘Ŗž®: (1 - ┌Š^2) ž│^2 + 2┌Š^2 ┘ü ž│ + žĄ^2 = ┌Š^2 ┘ü
┘ģž╣ž¦ž»┘äž® ┘ģ┘å ž¦┘äž»ž▒ž¼ž® ž¦┘äž½ž¦┘å┘Ŗž® ┘ü┘Ŗ ┘ģž¬ž║┘Ŗž▒┘Ŗ┘å ž│žī žĄ ┘ł┘Ŗ┘ģ┘ā┘å ┘āž¬ž¦ž©ž® ┘ćž░┘ć ž¦┘ä┘ģž╣ž¦ž»┘äž® ž╣┘ä┘ē ž¦┘䞥┘łž▒ž® ž¦┘䞬ž¦┘ä┘Ŗž®: žŻ ž│^2 + 2ž© ž│ žĄ + ž¼┘Ć žĄ^2 + 2ž» ž│ + 2┌Š žĄ + ┘ł = 0
┘ü┘Ŗ ž¦┘ä┘åžĖž¦┘ģ ž¦┘äžźžŁž»ž¦ž½┘Ŗ ž¦┘äž»┘Ŗ┘āž¦ž▒ž¬┘Ŗ ┘Ŗ┘ā┘ł┘å ┘ģ┘åžŁ┘å┘ē ž»ž¦┘äž® ž¬ž▒ž©┘Ŗž╣┘Ŗž® ┘ü┘Ŗ ┘ģž¬ž║┘Ŗž▒┘Ŗ┘å ž»┘ł┘ģž¦ ┘éžĘž╣ž¦ ┘ģž«ž▒┘łžĘ┘Ŗž¦žī ┘ł┘ā┘ä ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® ž¬ž¬┘ā┘ł┘å ž©┘ćž░┘ć ž¦┘äžĘž▒┘Ŗ┘éž®. ┘ģž╣ž¦ž»┘䞬┘枦 ž¬┘ā┘ł┘å ┘ü┘Ŗ ž¦┘䞥┘łž▒ž®:
A
x
2
+
B
x
y
+
C
y
2
+
D
x
+
E
y
+
F
=
0
{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
┘åžŁž│ž© ž¦┘ä┘ģ┘ģ┘Ŗ┘æž▓
B
2
− ŌłÆ -->
4
A
C
{\displaystyle B^{2}-4AC}
žźž░ž¦ ┘āž¦┘å
B
2
− ŌłÆ -->
4
A
C
<
0
{\displaystyle B^{2}-4AC<0}
┘éžĘž╣ ┘垦┘鞥 (┘ģž¦┘ä┘ģ ┘Ŗ┘ā┘å ž¦┘ä┘ģž«ž▒┘łžĘ ┘ģ┘åžŁ┘䞦žī ┘ģž½┘ä┘ŗž¦
x
2
+
y
2
+
10
=
0
{\displaystyle x^{2}+y^{2}+10=0}
žźž░ž¦ ┘āž¦┘å
A
=
C
{\displaystyle A=C}
B
=
0
{\displaystyle B=0}
ž»ž¦ž”ž▒ž® žø
žźž░ž¦ ┘āž¦┘å
B
2
− ŌłÆ -->
4
A
C
=
0
{\displaystyle B^{2}-4AC=0}
┘éžĘž╣ ┘ģ┘āž¦┘üž” .
žźž░ž¦ ┘āž¦┘å
B
2
− ŌłÆ -->
4
A
C
>
0
{\displaystyle B^{2}-4AC>0}
┘éžĘž╣ ž▓ž¦ž”ž» .
┘䞦žŁžĖ žŻ┘å A ┘ł B ┘ć┘Ŗ ┘ģž╣ž¦┘ģ┘䞦ž¬ ┘䞦 ž¬┘ģž½┘ä žŻ┘Ŗ žŻžĘ┘łž¦┘ä ┘ä┘ä┘ģžŁž¦┘łž▒ ž¦┘䞯┘āž©ž▒ ┘łž¦┘䞯žĄž║ž▒ ┘ā┘ģž¦ ž│┘Ŗž¬┘ģ ž¬ž╣ž▒┘Ŗ┘ü┘枦 ┘ü┘Ŗ ž¦┘ä┘éž│┘ģ ž¦┘䞬ž¦┘ä┘Ŗ
┘ü┘Ŗ ž¬ž╣ž©┘Ŗž▒ ž¦┘ä┘ģžĄ┘ü┘ł┘üž¦ž¬ ž¬žĄž©žŁ ž¦┘ä┘ģž╣ž¦ž»┘䞦ž¬ ž¦┘äž│ž¦ž©┘éž® ┘āž¦┘䞬ž¦┘ä┘Ŗ:
[
x
y
]
.
[
A
B
/
2
B
/
2
C
]
.
[
x
y
]
+
D
x
+
E
y
+
F
=
0.
{\displaystyle {\begin{bmatrix}x&y\end{bmatrix}}.{\begin{bmatrix}A&B/2\\B/2&C\end{bmatrix}}.{\begin{bmatrix}x\\y\end{bmatrix}}+Dx+Ey+F=0.}
žŻ┘ł
[
x
y
1
]
.
[
A
B
/
2
D
/
2
B
/
2
C
E
/
2
D
/
2
E
/
2
F
]
.
[
x
y
1
]
=
0.
{\displaystyle {\begin{bmatrix}x&y&1\end{bmatrix}}.{\begin{bmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{bmatrix}}.{\begin{bmatrix}x\\y\\1\end{bmatrix}}=0.}
┘ł
B
2
− ŌłÆ -->
4
A
C
=
− ŌłÆ -->
4
|
A
B
/
2
B
/
2
C
|
{\displaystyle B^{2}-4AC=-4\left|{\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right|}
ž▒ž║┘ģ ž¬ž║┘Ŗ┘Ŗž▒ ž¦┘äžźžŁž»ž¦ž½┘Ŗž¦ž¬ ┘Ŗ┘ģ┘ā┘å ┘łžČž╣ ┘ćž░┘ć ž¦┘ä┘ģž╣ž¦ž»┘䞦ž¬ ┘ü┘Ŗ žĄ┘łž▒ž® ┘é┘Ŗž¦ž│┘Ŗž®:
ž¦┘äž»ž¦ž”ž▒ž®:
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}\,}
ž¦┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥:
x
2
a
2
+
y
2
b
2
=
1
,
x
2
b
2
+
y
2
a
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1,\;{x^{2} \over b^{2}}+{y^{2} \over a^{2}}=1}
ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģ┘āž¦┘üž”:
y
2
=
4
a
x
{\displaystyle y^{2}=4ax\,}
x
2
=
4
a
y
{\displaystyle x^{2}=4ay\,}
ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž»:
x
2
a
2
− ŌłÆ -->
y
2
b
2
=
1
,
x
2
b
2
− ŌłÆ -->
y
2
a
2
=
− ŌłÆ -->
1
{\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1,\;{x^{2} \over b^{2}}-{y^{2} \over a^{2}}=-1}
ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž» ž¦┘ä┘鞦ž”┘ģ:
x
y
=
c
2
{\displaystyle xy=c^{2}\,}
┘ģž½┘ä ┘ćž░┘ć ž¦┘䞥┘Ŗž║ ž¬┘ā┘ł┘å ┘ģž¬┘ģž¦ž½┘äž® žŁ┘ł┘ä ┘ģžŁ┘łž▒ x žī ┘ł┘ü┘Ŗ┘ģž¦ ┘Ŗž«žĄ┘Å┘æ ž¦┘äž»ž¦ž”ž▒ž® ┘łž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž» ┘łž¦┘ä┘垦┘鞥 žŁ┘ł┘ä ┘ģžŁ┘łž▒ y ┘ł
ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž» ž¦┘ä┘鞦ž”┘ģ ┘ć┘Ŗ žŁž¦┘äž® ž¦┘䞬┘ģž¦ž½┘ä ž¦┘ä┘łžŁ┘Ŗž»ž® ž¦┘䞬┘Ŗ ž¬┘ā┘ł┘å žŁ┘ł┘ä
y
=
x
{\displaystyle y=x}
y
=
− ŌłÆ -->
x
{\displaystyle y=-x}
┘Ŗ┘ģ┘ā┘å ┘āž¬ž¦ž©ž® ┘ćž░┘ć ž¦┘䞥┘Ŗž║ ž¦┘ä┘é┘Ŗž¦ž│┘Ŗž® ┘ü┘Ŗ žĄ┘łž▒ž® ┘ģž╣ž¦ž»┘䞦ž¬ ┘łž│┘ŖžĘ┘Ŗž® (ž©ž¦ž▒ž¦┘ģž¬ž▒┘Ŗž®):
ž¦┘äž»ž¦ž”ž▒ž®:
(
a
cos
ŌüĪ -->
θ ╬Ė -->
,
a
sin
ŌüĪ -->
θ ╬Ė -->
)
{\displaystyle (a\cos \theta ,a\sin \theta )}
ž¦┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥:
(
a
cos
ŌüĪ -->
θ ╬Ė -->
,
b
sin
ŌüĪ -->
θ ╬Ė -->
)
{\displaystyle (a\cos \theta ,b\sin \theta )}
ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģ┘āž¦┘üž”:
(
a
t
2
,
2
a
t
)
{\displaystyle (at^{2},2at)}
ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž»:
(
a
sec
ŌüĪ -->
θ ╬Ė -->
,
b
tan
ŌüĪ -->
θ ╬Ė -->
)
{\displaystyle (a\sec \theta ,b\tan \theta )}
(
± ┬▒ -->
a
cosh
ŌüĪ -->
u
,
b
sinh
ŌüĪ -->
u
)
{\displaystyle (\pm a\cosh u,b\sinh u)}
ž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž» ž¦┘ä┘鞦ž”┘ģ:
(
c
t
,
c
t
)
{\displaystyle \left(ct,{c \over t}\right)}
┘ü┘Ŗ ž¦┘äžźžŁž»ž¦ž½┘Ŗž¦ž¬ ž¦┘ä┘ģž¬ž¼ž¦┘åž│ž®žī ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ┘Ŗ┘ģ┘ā┘å ž¬┘ģž½┘Ŗ┘ä┘枦 ┘āž¦┘䞬ž¦┘ä┘Ŗ:
A
1
x
2
+
A
2
y
2
+
A
3
z
2
+
2
B
1
x
y
+
2
B
2
x
z
+
2
B
3
y
z
=
0.
{\displaystyle A_{1}x^{2}+A_{2}y^{2}+A_{3}z^{2}+2B_{1}xy+2B_{2}xz+2B_{3}yz=0.}
žŻ┘ł ž©ž¬ž╣ž©┘Ŗž▒ ž¦┘ä┘ģžĄ┘ü┘ł┘üž¦ž¬ :
[
x
y
z
]
.
[
A
1
B
1
B
2
B
1
A
2
B
3
B
2
B
3
A
3
]
.
[
x
y
z
]
=
0.
{\displaystyle {\begin{bmatrix}x&y&z\end{bmatrix}}.{\begin{bmatrix}A_{1}&B_{1}&B_{2}\\B_{1}&A_{2}&B_{3}\\B_{2}&B_{3}&A_{3}\end{bmatrix}}.{\begin{bmatrix}x\\y\\z\end{bmatrix}}=0.}
ž¦┘ä┘ģžĄ┘ü┘ł┘üž®
M
=
[
A
1
B
1
B
2
B
1
A
2
B
3
B
2
B
3
A
3
]
{\displaystyle M={\begin{bmatrix}A_{1}&B_{1}&B_{2}\\B_{1}&A_{2}&B_{3}\\B_{2}&B_{3}&A_{3}\end{bmatrix}}}
Δ ╬ö -->
=
det
(
M
)
=
det
(
[
A
1
B
1
B
2
B
1
A
2
B
3
B
2
B
3
A
3
]
)
{\displaystyle \Delta =\det(M)=\det \left({\begin{bmatrix}A_{1}&B_{1}&B_{2}\\B_{1}&A_{2}&B_{3}\\B_{2}&B_{3}&A_{3}\end{bmatrix}}\right)}
┘ģžŁž»ž»ž® ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ. žźž░ž¦ ┘āž¦┘å ╬ö = 0 ┘üžź┘å ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ┘Ŗž│┘ģ┘ē ┬½┘ģ┘åžŁ┘ä┘ŗž¦ Degenerate┬╗žī ┘ł┘ćž░ž¦ ┘Ŗž╣┘å┘Ŗ žŻ┘å┘ć ┘ü┘Ŗ ž¦┘䞣┘é┘Ŗ┘éž® ž╣ž©ž¦ž▒ž® ž╣┘å ž¦ž¬žŁž¦ž» ž«žĘ┘Ŗ┘å ┘ģž│ž¬┘é┘Ŗ┘ģ┘Ŗ┘å. žŻ┘Ŗ ┘éžĘž╣ ┘ģž«ž▒┘łžĘ┘Ŗ ┘Ŗž¬┘鞦žĘž╣ ┘ģž╣ ┘å┘üž│┘ć ┘ć┘ł ┘éžĘž╣ ┘ģ┘åžŁ┘äž®žī ┘ł┘ä┘ā┘å ┘ä┘Ŗž│ ┘ā┘ä ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģ┘åžŁ┘äž® ž¬┘鞦žĘž╣ ┘å┘üž│┘枦žī ┘ł┘ü┘Ŗ ┘ćž░┘ć ž¦┘䞣ž¦┘äž® ┘Ŗ┘ā┘ł┘å ž¦┘ä┘éžĘž╣ ž«žĘ┘ŗž¦ ┘ģž│ž¬┘é┘Ŗ┘ģž¦┘ŗ.
ž╣┘ä┘ē ž│ž©┘Ŗ┘ä ž¦┘ä┘ģž½ž¦┘ä ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ
[
x
y
z
]
.
[
1
0
0
0
− ŌłÆ -->
1
0
0
0
0
]
.
[
x
y
z
]
=
0
{\displaystyle {\begin{bmatrix}x&y&z\end{bmatrix}}.{\begin{bmatrix}1&0&0\\0&-1&0\\0&0&0\end{bmatrix}}.{\begin{bmatrix}x\\y\\z\end{bmatrix}}=0}
{
x
2
− ŌłÆ -->
y
2
=
0
}
=
{
(
x
+
y
)
(
x
− ŌłÆ -->
y
)
=
0
}
=
{
x
+
y
=
0
}
∪ Ōł¬ -->
{
x
− ŌłÆ -->
y
=
0
}
{\displaystyle \{x^{2}-y^{2}=0\}=\{(x+y)(x-y)=0\}=\{x+y=0\}\cup \{x-y=0\}}
┘łž©ž¦┘ä┘ģž½┘ä ┘Ŗž«ž¬ž▓┘ä ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ žŻžŁ┘Ŗž¦┘å┘ŗž¦ ž«žĘ┘ŗž¦ ┘ģ┘üž▒ž»ž¦:
{
x
2
+
2
x
y
+
y
2
=
0
}
=
{
(
x
+
y
)
2
=
0
}
=
{
x
+
y
=
0
}
∪ Ōł¬ -->
{
x
+
y
=
0
}
=
{
x
+
y
=
0
}
{\displaystyle \{x^{2}+2xy+y^{2}=0\}=\{(x+y)^{2}=0\}=\{x+y=0\}\cup \{x+y=0\}=\{x+y=0\}}
δ ╬┤ -->
=
det
(
[
A
1
B
1
B
1
A
2
]
)
{\displaystyle \delta =\det \left({\begin{bmatrix}A_{1}&B_{1}\\B_{1}&A_{2}\end{bmatrix}}\right)}
1 = A2 ┘ü┘ć┘Ŗ ž»ž¦ž”ž▒ž®žī žŻ┘ģž¦ žźž░ž¦ ┘āž¦┘å ╬┤<0 ┘ł A1 == -A2 ┘ü┘ć┘ł ┘éžĘž╣ ž▓ž¦ž”ž» ┘鞦ž”┘ģ. ┘Ŗ┘ģ┘ā┘å ž¦ž½ž©ž¦ž¬ žŻ┘å┘ć ┘ü┘Ŗ ┘ģž│ž¬┘ł┘ē ž¦┘äžźž│┘鞦žĘ ž¦┘ä┘ģž▒┘āž© CP2 ┘éžĘž╣┘Ŗ┘å ┘ģž«ž▒┘łžĘ┘Ŗ┘Ŗ┘å ž©┘Ŗ┘å┘ć┘ģž¦ 4 ┘å┘鞦žĘ ┘ģž┤ž¬ž▒┘āž® (žźž░ž¦ žŻž«ž░┘垦 ┘ü┘Ŗ ž¦┘䞦ž╣ž¬ž©ž¦ž▒ ž¦┘䞬ž╣ž»ž»┘Ŗž® Multiplicity) žŻ┘Ŗ ┘䞦 ┘Ŗ┘łž¼ž» žŻ┘āž½ž▒ ┘ģ┘å 4 ┘å┘鞦žĘ ž¬┘鞦žĘž╣ ┘łž¬┘łž¼ž» ž»ž¦ž”┘ģ┘ŗž¦ ┘å┘éžĘž® ž¬┘鞦žĘž╣ ┘łž¦žŁž»ž® (ž¦┘䞦žŁž¬┘ģž¦┘䞦ž¬: 4 ┘å┘鞦žĘ ž¬┘鞦žĘž╣ ┘ģž«ž¬┘ä┘üž®žī žŻ┘ł ┘å┘éžĘž¬┘Ŗ ž¬┘鞦žĘž╣ ┘üž▒ž»┘Ŗž¬┘Ŗ┘å ┘ł┘å┘éžĘž® ž¬┘鞦žĘž╣ ┘ģž▓ž»┘łž¼žī žŻ┘ł ┘å┘éžĘž¬┘Ŗ ž¬┘鞦žĘž╣ ┘ģž▓ž»┘łž¼žī žŻ┘ł ┘å┘éžĘž® ž¬┘鞦žĘž╣ ┘üž▒ž»┘Ŗ ┘ł┘å┘éžĘž® ž¬┘鞦žĘž╣ ž©ž¬ž╣ž»ž»┘Ŗž® 3žī žŻ┘ł ┘å┘éžĘž® ž¬┘鞦žĘž╣ ┘łž¦žŁž»ž® ž©ž¬ž╣ž»ž»┘Ŗž® 4). žźž░ž¦ ┘łž¼ž»ž¬ ┘å┘éžĘž® ž¬┘鞦žĘž╣ ┘łž¦žŁž»ž® ž╣┘ä┘ē ž¦┘䞯┘é┘ä ž░ž¦ž¬ ž¬ž╣ž»ž»┘Ŗž® > 1 ┘Ŗ┘鞦┘ä žŻ┘å ž¦┘ä┘éžĘž╣┘Ŗ┘å ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ┘Ŗ┘å ┘ģž¬┘ģž¦ž│┘Ŗ┘å . žŻ┘ģž¦ žźž░ž¦ ┘āž¦┘å ┘ć┘垦┘ā ┘å┘éžĘž® ž¬┘鞦žĘž╣ ┘łž¦žŁž»ž® ž░ž¦ž¬ ž¬ž╣ž»ž»┘Ŗž® 4 ┘Ŗ┘鞦┘ä žŻ┘å ž¦┘ä┘éžĘž╣┘Ŗ┘å ┘ģž¬┘䞦┘ģž│┘Ŗ┘å osculating.
žźžČž¦┘üž® ┘ä┘ģž¦ ž│ž©┘é ┘üžź┘å ┘ā┘ä ž«žĘ ┘ģž│ž¬┘é┘Ŗ┘ģ ┘Ŗ┘鞦žĘž╣ ┘ā┘ä ┘ģ┘å ž¦┘ä┘éžĘž╣┘Ŗ┘å ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ┘Ŗ┘å ┘ģž▒ž¬┘Ŗ┘å. žźž░ž¦ ┘āž¦┘垬 ┘å┘éžĘž® ž¦┘䞬┘鞦žĘž╣ ┘ģž▓ž»┘łž¼ž® ž╣┘Åž»┘Ä┘æ ž¦┘äž«žĘ ┘ģ┘ģž¦ž│┘ŗž¦ ┘ł┘Ŗž│┘ģ┘ē ž¦┘ä┘ģ┘ģž¦ž│ . ┘䞯┘å ┘ā┘ä ┘ģž│ž¬┘é┘Ŗ┘ģ ┘Ŗ┘鞦žĘž╣ ž¦┘ä┘éžĘž╣ ┘ģž▒ž¬┘Ŗ┘å ┘üžź┘å ┘ā┘䞦 ž¦┘ä┘éžĘž╣┘Ŗ┘å ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ┘Ŗ┘å ┘ä┘ć ┘å┘éžĘž¬┘Ŗ┘å ┘ü┘Ŗ ┘ģž¦┘䞦┘å┘枦┘Ŗž® (ž¬┘鞦žĘž╣ ž¦┘ä┘å┘鞦žĘ ┘ģž╣ ž«žĘ ž¦┘ä┘ģž¦┘䞦┘å┘枦┘Ŗž®) ┘üžźž░ž¦ ┘āž¦┘垬 ž¦┘ä┘å┘éžĘž¬ž¦┘å žŁ┘é┘Ŗ┘é┘Ŗž¬ž¦┘å ┘ü┘䞦ž©ž» žŻ┘å ┘Ŗ┘ā┘ł┘å ž¦┘ä┘éžĘž╣ ž▓ž¦ž”ž»┘ŗž¦žī ┘łžźž░ž¦ ┘āž¦┘垬ž¦ ž¬ž«┘Ŗ┘ä┘Ŗž¬┘Ŗ┘å ┘ü┘䞦ž©ž» žŻ┘å ┘Ŗ┘ā┘ł┘å ž¦┘ä┘éžĘž╣ ┘垦┘鞥┘ŗž¦žī žŻ┘ģž¦ žźž░ž¦ ┘āž¦┘å ┘ä┘ä┘éžĘž╣ ┘å┘éžĘž® ┘łž¦žŁž»ž® ┘ģž▓ž»┘łž¼ž® ┘ü┘Ŗ ┘ģž¦┘䞦┘å┘枦┘Ŗž® ┘ü┘ć┘ł ┘ģ┘āž¦┘üž”.
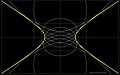
ž¦┘åžĖž▒ žź┘ä┘ē ž¬žĘž©┘Ŗ┘鞦ž¬ ž¦┘äž»ž¦ž”ž▒ž® ┘łž¦┘ä┘éžĘž╣ ž¦┘ä┘垦┘鞥 ┘łž¦┘ä┘éžĘž╣ ž¦┘ä┘ģ┘āž¦┘üž” ┘łž¦┘ä┘éžĘž╣ ž¦┘äž▓ž¦ž”ž» .
┘Ŗž╣ž¬┘éž» žŻ┘å ž¦┘䞬ž╣ž▒┘Ŗ┘ü ž¦┘䞯┘ł┘ä ┘ä┘éžĘž╣ ┘ģž«ž▒┘łžĘ┘Ŗ ┘éž»┘ģ┘ć ┘ģ┘Ŗ┘垦┘Ŗž«┘ģ┘łž│ (ž¬┘ł┘ü┘Ŗ 320 ┘éž©┘ä ž¦┘ä┘ģ┘Ŗ┘䞦ž») ┘āž¼ž▓žĪ ┘ģ┘å žŁ┘ä┘ć ┘ä┘ģž╣žČ┘äž® ž»┘Ŗ┘ä┘Ŗž® (┘ģžČž¦ž╣┘üž® ž¦┘ä┘ģ┘āž╣ž© ).[ 2] [ 3] [ 4] ┘ģ┘ł┘äž» ž¦┘äž│žĘžŁ ). žŁ┘Åž»┘É┘æž»ž¬ ž½┘䞦ž½ž® žŻ┘å┘łž¦ž╣ ┘ģ┘å ž¦┘ä┘ģž«ž¦ž▒┘ŖžĘ ┘ģ┘å ž«┘䞦┘ä ž▓┘łž¦┘Ŗž¦ ┘é┘ģž® ž¦┘äž▒žŻž│ (ž¬┘鞦ž│ žČž╣┘ü ž¦┘äž▓ž¦┘ł┘Ŗž® ž¦┘䞬┘Ŗ ž┤┘ā┘ä┘枦 ┘łž¬ž▒ ž¦┘ä┘ģž½┘äž½ ┘łž¦┘äž│ž¦┘é ž¦┘䞬┘Ŗ ž¬ž»┘łž▒ žŁ┘ł┘ä┘枦 ┘ü┘Ŗ ž¦┘ä┘ģž½┘äž½ ž¦┘ä┘鞦ž”┘ģ). ž½┘ģ žŁ┘Åž»┘É┘æž» ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗ ž╣┘å žĘž▒┘Ŗ┘é ž¬┘鞦žĘž╣ žŻžŁž» ┘ćž░┘ć ž¦┘ä┘ģž«ž¦ž▒┘ŖžĘ ┘ģž╣ ┘ģž│ž¬┘ł┘Ŗ ┘ģž▒ž│┘ł┘ģ ž╣┘ģ┘łž»┘Ŗ┘ŗž¦ ž╣┘ä┘ē ž¦┘ä┘ģ┘ł┘äž». ┘Ŗž¬┘ģ ž¬žŁž»┘Ŗž» ┘å┘łž╣ ž¦┘ä┘éžĘž╣ ┘ģ┘å ž«┘䞦┘ä ┘å┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘžī žŻ┘Ŗ ┘ģ┘å ž«┘䞦┘ä ž¦┘äž▓ž¦┘ł┘Ŗž® ž¦┘ä┘ģž¬ž┤┘ā┘äž® ┘ü┘Ŗ ┘é┘ģž® ž¦┘ä┘ģž«ž▒┘łžĘ: žźž░ž¦ ┘āž¦┘垬 ž¦┘äž▓ž¦┘ł┘Ŗž® žŁž¦ž»ž®žī ┘üžź┘å ž¦┘ä┘éžĘž╣ ž╣ž©ž¦ž▒ž® ž╣┘å ┘éžĘž╣ ┘垦┘鞥žø žźž░ž¦ ┘āž¦┘垬 ž¦┘äž▓ž¦┘ł┘Ŗž® ┘鞦ž”┘ģž®žī ┘üžź┘å ž¦┘ä┘éžĘž╣ ž╣ž©ž¦ž▒ž® ž╣┘å ┘éžĘž╣ ┘ģ┘āž¦┘üž”žø ┘łžźž░ž¦ ┘āž¦┘垬 ž¦┘äž▓ž¦┘ł┘Ŗž® ┘ģ┘å┘üž▒ž¼ž®žī ┘üžź┘å ž¦┘ä┘ģž«ž▒┘łžĘ ž╣ž©ž¦ž▒ž® ž╣┘å ┘éžĘž╣ ž▓ž¦ž”ž» (┘ł┘ä┘ā┘å ┘ü┘éžĘ ┘üž▒ž╣ ┘łž¦žŁž» ┘ģ┘å ž¦┘ä┘ģ┘åžŁ┘å┘ē).[ 5]
┘Ŗ┘鞦┘ä žŻ┘å žź┘é┘ä┘Ŗž»ž│ (žŁ┘łž¦┘ä┘Ŗ 300 ┘éž©┘ä ž¦┘ä┘ģ┘Ŗ┘䞦ž») ┘āž¬ž© žŻž▒ž©ž╣ž® ┘āž¬ž© ž╣┘å ž¦┘ä┘ģž«ž¦ž▒┘ŖžĘ ┘ł┘ä┘ā┘å ┘ü┘éž»ž¬ žŻ┘ŖžČ┘ŗž¦.[ 6] žŻž▒ž«┘ģ┘Ŗž»ž│ (ž¬┘ł┘ü┘Ŗ ž╣ž¦┘ģ 212 ┘é.┘ģ) ž»ž▒ž│ ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž®žī ž©ž╣ž» žŻ┘å žŁž»ž» ┘ģž│ž¦žŁž® ž¦┘ä┘ģ┘åžĘ┘éž® ž¦┘䞬┘Ŗ ┘ŖžŁž»┘枦 ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģ┘āž¦┘üž” ┘łž¦┘ä┘łž¬ž▒ ┘ü┘Ŗ ┘āž¬ž¦ž©┘ć ┬½ž¬ž▒ž©┘Ŗž╣ ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģ┘āž¦┘üž” ┬╗. ┘āž¦┘å ž¦┘枬┘ģž¦┘ģ┘ć ž¦┘äž▒ž”┘Ŗž│┘Ŗ ┘Ŗž¬ž╣┘ä┘é ž©┘é┘Ŗž¦ž│ ┘ģž│ž¦žŁž¦ž¬ ┘łžŁž¼┘ł┘ģ ž¦┘䞯ž┤┘āž¦┘ä ž¦┘ä┘ģž¬ž╣┘ä┘éž® ž©ž¦┘ä┘éžĘ┘łž╣ ┘łž©┘é┘Ŗ ž¼ž▓žĪ ┘ģ┘å ┘ćž░ž¦ ž¦┘äž╣┘ģ┘ä ž╣┘ä┘ē ┘é┘Ŗž» ž¦┘䞣┘Ŗž¦ž® ┘ü┘Ŗ ┘āž¬ž¦ž©┘ć ž╣┘å ž¦┘ä┘ģž¼ž│┘ģž¦ž¬ ž¦┘äž»┘łž▒ž¦┘å┘Ŗž® ┘ä┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® ┬½ž╣┘å žŻž┤ž©ž¦┘ć ž¦┘ä┘ģž«ž▒┘łžĘ ┘łž¦┘äž│žĘ┘łžŁ ž¦┘ä┘āž▒┘ł┘Ŗž®┬╗.[ 7]
┘ģž«žĘ┘łžĘž®┘ī ┘䞬ž▒ž¼┘ģž®┘Ź ž╣ž▒ž©┘Ŗž®┘Ź ┘ģ┘å ┘āž¬ž¦ž© ┬½ž¦┘ä┘ģž«ž¦ž▒┘ŖžĘ┬╗ ┘䞯ž©┘ł┘ä┘ł┘å┘Ŗ┘łž│. ┘Ŗž▒ž¼ž╣ žŻž╣žĖ┘ģ ž¬┘éž»┘ģ ┘ü┘Ŗ ž»ž▒ž¦ž│ž® ž¦┘ä┘ģž«ž¦ž▒┘ŖžĘ ┘ģ┘å ┘éž©┘ä ž¦┘äžźž║ž▒┘Ŗ┘é žź┘ä┘ē žŻž©┘ä┘ł┘å┘Ŗ┘łž│ ž¦┘äž©ž▒ž║ž¦┘ł┘Ŗ (ž¬┘ł┘ü┘Ŗ ž╣ž¦┘ģ 190 ┘é.┘ģ)žī ž¦┘äž░┘Ŗ ž¬┘äž«žĄ ┘āž¬ž¦ž©┘ć ž╣┘å ž¦┘ä┘ģž«ž¦ž▒┘ŖžĘ ž¦┘ä┘ģ┘ā┘ł┘åž® ┘ģ┘å ž½┘ģž¦┘å┘Ŗž® ┘ģž¼┘äž»ž¦ž¬ ┘łž¬┘łž│┘É┘æž╣ ž¦┘ä┘ģž╣ž▒┘üž® ž¦┘ä┘ģ┘łž¼┘łž»ž® žź┘ä┘ē žŁž» ┘āž©┘Ŗž▒.[ 8] ellipse žī ┘ł parabola ┘ł hyperbola žī ┘łž¦ž│ž¬ž╣ž¦ž▒ ž¦┘ä┘ģžĄžĘ┘䞣ž¦ž¬ ┘ģ┘å žŻž╣┘ģž¦┘ä ┘ü┘Ŗž½ž¦ž║┘łž▒ž│ ž¦┘äž│ž¦ž©┘éž® žŁ┘ł┘ä ž¦┘ä┘ģž│ž¦žŁž¦ž¬.[ 9]
┘Ŗž╣┘łž» ž¦┘ä┘üžČ┘ä žź┘ä┘ē ž©ž©ž│ ž¦┘äž▒┘ł┘ģ┘Ŗ (ž¬┘ł┘ü┘Ŗ ž╣ž¦┘ģ 350 ┘ģ) ┘ü┘Ŗ ž┤ž▒žŁ žŻ┘ć┘ģ┘Ŗž® ┘ģ┘ü┘ć┘ł┘ģ ž©žżž▒ž® ž¦┘ä┘éžĘž╣žī ┘łž¬┘üžĄ┘Ŗ┘ä ┘ģ┘ü┘ć┘ł┘ģ ž░┘Ŗ ž¦┘䞥┘äž® ž©ž¦┘äž»┘ä┘Ŗ┘ä (Directrix)žī ž©┘ģž¦ ┘ü┘Ŗ ž░┘ä┘ā žŁž¦┘äž® ž¦┘ä┘éžĘž╣ ž¦┘ä┘ģ┘āž¦┘üž” (ž¦┘äž░┘Ŗ ┘Ŗ┘üž¬┘éž▒ žź┘ä┘Ŗ┘ć žŻž╣┘ģž¦┘ä žŻž©┘ä┘ł┘å┘Ŗ┘łž│ ž¦┘ä┘ģž╣ž▒┘ł┘üž®).[ 10]
ž¬┘ģ ┘łžĄ┘ü žŻž»ž¦ž® ┘äž▒ž│┘ģ ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® ┘䞯┘ł┘ä ┘ģž▒ž® ž╣ž¦┘ģ 1000 ┘ģ ┘ģ┘å ┘éž©┘ä ž╣ž¦┘ä┘ģ ž¦┘äž▒┘Ŗž¦žČ┘Ŗž¦ž¬ ž¦┘ä┘ģž│┘ä┘ģ žŻž©┘ł ž│┘ć┘ä ž¦┘ä┘é┘ł┘ć┘Ŗ .[ 11] [ 12]
ž¬┘Åž▒ž¼┘É┘ģž¬ žŻž╣┘ģž¦┘ä žŻž©┘ä┘ł┘å┘Ŗ┘łž│ žź┘ä┘ē ž¦┘ä┘äž║ž® ž¦┘äž╣ž▒ž©┘Ŗž®žī ┘ł┘ä┘ģ ┘Ŗž©┘é ž¦┘ä┘āž½┘Ŗž▒ ┘ģ┘å žŻž╣┘ģž¦┘ä┘ć žź┘䞦 ž¦┘ä┘åž│ž«ž® ž¦┘äž╣ž▒ž©┘Ŗž®. ┘łž¼ž» ž¦┘äž╣┘ä┘ģž¦žĪ ž¦┘ä┘ģž│┘ä┘ģ┘Ŗ┘å ž¬žĘž©┘Ŗ┘鞦ž¬ ž¦┘ä┘åžĖž▒┘Ŗž®žī žŻž©ž▒ž▓┘枦 ž╣ž¦┘ä┘ģ ž¦┘äž▒┘Ŗž¦žČ┘Ŗž¦ž¬ ┘łž¦┘äž┤ž¦ž╣ž▒ ž¦┘ä┘ģž│┘ä┘ģ ž╣┘ģž▒ ž¦┘äž«┘Ŗž¦┘ģ žī ž¦┘äž░┘Ŗ ž¦ž│ž¬ž«ž»┘ģ ┘éžĘ┘łž╣┘ŗž¦ ┘ģž«ž▒┘łžĘ┘Ŗž® ┘䞣┘ä ž¦┘ä┘ģž╣ž¦ž»┘䞦ž¬ ž¦┘äž¼ž©ž▒┘Ŗž® ž¦┘䞬┘Ŗ ┘䞦 ž¬ž▓┘Ŗž» ž╣┘å ž½┘䞦ž½ ž»ž▒ž¼ž¦ž¬.[ 13] [ 14]
┘ģž»┘æž» ┘Ŗ┘ł┘枦┘åž│ ┘ā┘Ŗž©┘äž▒ ┘åžĖž▒┘Ŗž® ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® ┘ģ┘å ž«┘䞦┘ä ┬½┘ģž©ž»žŻ ž¦┘䞦ž│ž¬┘ģž▒ž¦ž▒┘Ŗž® ┬╗žī ┘ģ┘éž»┘ģž® ┘ä┘ģ┘ü┘ć┘ł┘ģ ž¦┘ä┘å┘枦┘Ŗž¦ž¬. ž¦ž│ž¬ž«ž»┘ģ ┘ā┘Ŗž©┘äž▒ ┘ģžĄžĘ┘䞣 foci ┬½ž¦┘äž©žżž▒┬╗ ┘䞯┘ł┘ä ┘ģž▒ž® ž╣ž¦┘ģ 1604.
žĘ┘łž▒ ž¼┘Ŗž▒ž¦ž▒ ž»┘Ŗž▓ž¦ž▒ž║ ┘łž©┘ä┘Ŗž▓ ž©ž¦ž│┘āž¦┘ä ┘åžĖž▒┘Ŗž® ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® ž©ž¦ž│ž¬ž«ž»ž¦┘ģ ž┤┘ā┘ä ┘éž»┘Ŗ┘ģ ┘ä┘ä┘ć┘åž»ž│ž® ž¦┘äžźž│┘鞦žĘ┘Ŗž® žī ┘ģ┘ģž¦ ž│ž¦ž╣ž» ž╣┘ä┘ē ž¬┘ł┘ü┘Ŗž▒ ž¦┘äž»┘üž╣ ┘äž»ž▒ž¦ž│ž® ┘ćž░ž¦ ž¦┘ä┘ģž¼ž¦┘ä ž¦┘äž¼ž»┘Ŗž». ž╣┘ä┘ē ┘łž¼┘ć ž¦┘äž«žĄ┘łžĄžī ž¦┘āž¬ž┤┘ü ž©ž¦ž│┘āž¦┘ä ┘ģž©ž▒┘ć┘åž® ž¬┘Åž╣ž▒┘ü ž©ž¦ž│┘ģ hexagrammum mysticum [ 15]
┘鞦┘ģ ┘ā┘ä ┘ģ┘å ž▒┘Ŗ┘å┘Ŗ┘ć ž»┘Ŗ┘āž¦ž▒ž¬ ┘łž©┘Ŗ┘Ŗž▒ ┘ü┘Ŗž▒┘ģž¦ž¬ ž©ž¬žĘž©┘Ŗ┘é ž¦┘ä┘ć┘åž»ž│ž® ž¦┘䞬žŁ┘ä┘Ŗ┘ä┘Ŗž® ž¦┘ä┘ģ┘āž¬ž┤┘üž® žŁž»┘Ŗž½┘ŗž¦ ž╣┘ä┘ē ž»ž▒ž¦ž│ž® ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž¦ž¬. ┘āž¦┘å ┘ä┘ćž░ž¦ ž¬žŻž½┘Ŗž▒ ž¦┘䞣ž» ┘ģ┘å ž¦┘ä┘ģž┤ž¦┘ā┘ä ž¦┘ä┘ć┘åž»ž│┘Ŗž® ┘ä┘ä┘ģž«ž▒┘łžĘ┘Ŗž¦ž¬ žź┘ä┘ē ┘ģž┤ž¦┘ā┘ä ┘ü┘Ŗ ž¦┘äž¼ž©ž▒. ┘ł┘ģž╣ ž░┘ä┘āžī ┘āž¦┘å ž¼┘ł┘å ┘łž¦┘ä┘Ŗž│ ┘ü┘Ŗ ┘āž¬ž¦ž©┘ć 1655 žŻžĘž▒┘łžŁž® Tractatus de sectionibus conicis ┘ć┘ł ž¦┘äž░┘Ŗ ž╣ž▒┘æ┘ü žŻ┘ł┘䞦┘ŗ ž¦┘ä┘éžĘ┘łž╣ ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž® ž╣┘ä┘ē žŻ┘å┘枦 ┘å┘ģž¦ž░ž¼ ┘ä┘ģž╣ž¦ž»┘䞦ž¬ ┘ģ┘å ž¦┘äž»ž▒ž¼ž® ž¦┘äž½ž¦┘å┘Ŗž®.[ 16] Elementa Curvarum Linearum ┘ä┘Ŗ┘ł┘枦┘å ž»┘Ŗ ┘ü┘Ŗž¬ ž©žź┘åž┤ž¦žĪ ┘ā┘Ŗž©┘äž▒ ž¦┘ä┘ā┘Ŗ┘å┘Ŗ┘ģž¦ž¬┘Ŗ┘ā┘Ŗ ┘ä┘ä┘éžĘ┘łž╣ ž½┘ģ ž¬žĘ┘ł┘Ŗž▒ ž¦┘ä┘ģž╣ž¦ž»┘䞦ž¬ ž¦┘äž¼ž©ž▒┘Ŗž®. ┘ł┘ÅžĄ┘É┘ü ┘ćž░ž¦ ž¦┘äž╣┘ģ┘äžī ž¦┘äž░┘Ŗ ┘Ŗž│ž¬ž«ž»┘ģ ┘ģ┘å┘ćž¼┘Ŗž® ┘ü┘Ŗž▒┘ģž¦ ┘łž¬ž»┘ł┘Ŗ┘å ž»┘Ŗ┘āž¦ž▒ž¬ ž©žŻ┘å┘ć žŻ┘ł┘ä ┘āž¬ž¦ž© žŁ┘ł┘ä ┘ćž░ž¦ ž¦┘ä┘ģ┘łžČ┘łž╣.[ 17] Directrix .[ 17]
ž¬žŁ┘ł┘ä ž▓ž¦ž”ž»┘Ŗ ┘ä┘éžĘž╣ ┘垦┘鞥. ž¦┘äž░┘Ŗ ┘Ŗ┘ģ┘ā┘å žŻ┘å ž¬┘ā┘ł┘å ž»ž¦┘äž® ž│žĘžŁ ┘ģ┘å ž¦┘äž»ž▒ž¼ž® ž¦┘äž½ž¦┘å┘Ŗž® (┘垦┘鞥žī ┘ģ┘āž¦┘üž” žī ž▓ž¦ž”ž»)
[ 18]
┘ģž╣┘ä┘ł┘ģ: ┘ģž«ž▒┘łžĘ┘Ŗž¬┘Ŗ┘å ┘ģž¬┘ģž¦ž│ž¬┘Ŗ┘åžī ┘ģžĘ┘ä┘łž©: ž¬žŁž»┘Ŗž» ž¦┘ä┘ģž«ž▒┘łžĘ ž¦┘äž░┘Ŗ ┘Ŗ┘ģž▒ ž©┘ć┘ģž¦.
ž¬žŁž»┘Ŗž» ž¦┘䞯┘å┘łž¦ž╣ ž¦┘äž½┘䞦ž½ž® ┘ģ┘å ž¦┘ä┘ģž«ž▒┘łžĘ┘Ŗž¦ž¬ (┘éžĘž╣ ┘垦┘鞥 ┘ł┘ģ┘āž¦┘üž” ┘łž▓ž¦ž”ž») ž©žŁ┘Ŗž½ ž¬ž¬┘ģž¦ž│ ┘ü┘Ŗ ┘å┘éžĘž® ž╣ž¦┘ģž® (ž║┘Ŗž▒ ┘ģžŁ┘łž▒┘Ŗž®) ž©ž¦ž│ž¬ž«ž»ž¦┘ģ žźž¼ž▒ž¦žĪž¦ž¬ ┘ć┘åž»ž│┘Ŗž® ┘łžĄ┘ü┘Ŗž®.
^ Brannan, Esplen & Gray 1999 žī žĄ┘üžŁž¦ž¬ 13ŌĆō16^ According to ┘ü┘ä┘łžĘž▒ž«ž│ this solution was rejected by Plato on the grounds that it could not be achieved using only straightedge and compass, however this interpretation of Plutarch's statement has come under criticism.Boyer 2004 žī p.14, footnote 14
^ Boyer 2004 žī žĄ┘üžŁž¦ž¬ 17ŌĆō18^ Boyer 2004 žī žĄ┘üžŁž® 18^ Katz 1998 žī žĄ┘üžŁž® 117^ Heath, T.L., The Thirteen Books of Euclid's Elements , Vol. I, Dover, 1956, pg.16
^ Eves 1963 žī žĄ┘üžŁž® 28^ Apollonius of Perga, Treatise on Conic Sections ž¬┘ł┘ģž¦ž│ ┘ä┘Ŗž¬┘ä ┘ć┘Ŗž½ (Cambridge: Cambridge University Press, 2013). ┘åž│ž«ž® ┘ģžŁ┘ü┘łžĖž® 19 ┘Ŗ┘ł┘å┘Ŗ┘ł 2020 ž╣┘ä┘ē ┘ģ┘ł┘éž╣ ┘łž¦┘Ŗ ž©ž¦┘ā ┘ģž┤┘Ŗ┘å .
^ Eves 1963 žī žĄ┘üžŁž® 30^ Boyer 2004 žī žĄ┘üžŁž® 36^ Stillwellžī John (2010). Mathematics and its history (žĘ. 3rd). New York: Springer. žĄ. 30 . ISBN :978-1-4419-6052-8 ^ "Apollonius of Perga Conics Books One to Seven" (PDF) . ┘ģžżž▒ž┤┘ü ┘ģ┘å ž¦┘䞯žĄ┘ä (PDF) ┘ü┘Ŗ 2013-05-17. ž¦žĘ┘äž╣ ž╣┘ä┘Ŗ┘ć ž©ž¬ž¦ž▒┘Ŗž« 2011-06-10 .^ Boyer, C. B. , & Merzbach, U. C. [┘äž║ž¦ž¬ žŻž«ž▒┘ē] , A History of Mathematics (Hoboken : John Wiley & Sons, Inc. , 1968), p. 219 . ┘åž│ž«ž® ┘ģžŁ┘ü┘łžĖž® 30 ┘Ŗ┘ł┘å┘Ŗ┘ł 2019 ž╣┘ä┘ē ┘ģ┘ł┘éž╣ ┘łž¦┘Ŗ ž©ž¦┘ā ┘ģž┤┘Ŗ┘å .^ Van der Waerden, B. L. [┘äž║ž¦ž¬ žŻž«ž▒┘ē] , Geometry and Algebra in Ancient Civilizations (ž©ž▒┘ä┘Ŗ┘å /┘枦┘Ŗž»┘äž©ž▒ž║ : Springer Verlag , 1983), p. 73 . ┘åž│ž«ž® ┘ģžŁ┘ü┘łžĖž® 2018-12-04 ž╣┘ä┘ē ┘ģ┘ł┘éž╣ ┘łž¦┘Ŗ ž©ž¦┘ā ┘ģž┤┘Ŗ┘å .^ Katz 1998 žī žĄ┘üžŁž® 126^ Boyer 2004 žī žĄ┘üžŁž® 110^ ž¦ ž© Boyer 2004 žī žĄ┘üžŁž® 114^ ž». žŁž│┘å ž¦┘äž╣┘Ŗž│┘ł┘Ŗ. ┘å┘ģž░ž¼ž® ┘łžĄ┘ü┘Ŗž® ┘åž│ž«ž® ┘ģžŁ┘ü┘łžĖž® 2023-01-31 ž╣┘ä┘ē ┘ģ┘ł┘éž╣ ┘łž¦┘Ŗ ž©ž¦┘ā ┘ģž┤┘Ŗ┘å .
┘ģž╣ž¼┘ģ ž¦┘äž▒┘Ŗž¦žČ┘Ŗž¦ž¬ - ž¬žŻ┘ä┘Ŗ┘ü ┘äž¼┘åž® ┘ģ┘å ž¦┘äž«ž©ž▒ž¦žĪ ┘ģ┘å ┘łž▓ž¦ž▒ž® ž¦┘䞬ž▒ž©┘Ŗž® ┘łž¦┘䞬ž╣┘ä┘Ŗ┘ģ - ž╣┘ģž¦┘å - žĘž©ž╣ž® ┘ģ┘āž¬ž©ž® ┘äž©┘垦┘å - ž│ž¦žŁž® ž▒┘Ŗž¦žČ ž¦┘䞥┘䞣/ ž©┘Ŗž▒┘łž¬ - 1980┘ģ.