AKS質數測試
|
Read other articles:

Catholic diocese in Ireland Diocese of Galway and KilmacduaghDioecesis Galviensis, Duacensis et FinaborensisDeoise na Gaillimhe, Chill Mhic Duaich agus Chill FhionnúrachCathedral of Our Lady Assumed into Heaven and St NicholasLocationCountryIrelandTerritoryParts of counties Mayo, Galway and ClareEcclesiastical provinceProvince of TuamMetropolitanArchdiocese of TuamStatisticsArea1,008 sq mi (2,610 km2)Population- Catholics105,707InformationDenominationRoman CatholicRiteLat...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2018) لمعانٍ أخرى، طالع مقاطعة بولك (توضيح). مقاطعة بولك الإحداثيات 37°37�...

American TV series or program DuelGenreQuiz showDirected byMark GentillePresented byMike GreenbergComposerDavid VanacoreCountry of originUnited StatesNo. of seasons2No. of episodes16ProductionExecutive producersGail BermanLloyd BraunChris CowanJean-Michel MichenaudCharles DuncombeDavid RosconvalFrancis VacherRunning time≈61 minutes (Dec. 17-18)≈44 minutes (All other episodes)Production companiesRocket Science LaboratoriesFrench TVBermanBraunOriginal releaseNetworkABCReleaseDecember 1...

広島ガス株式会社HIROSHIMA GAS CO.,LTD. 本社種類 株式会社市場情報 東証プライム 95352000年3月1日上場 本社所在地 日本〒734-8555広島県広島市南区皆実町二丁目7番1号設立 1909年10月業種 電気・ガス業法人番号 2240001009205 代表者 代表取締役会長 田村興造代表取締役 社長執行役員 松藤研介資本金 51億81百万円発行済株式総数 67,998,590株売上高 連結822億円6,800万円(2019年3月)純資産

CikondangDesaNegara IndonesiaProvinsiJawa BaratKabupatenCianjurKecamatanCibeberKode Kemendagri32.03.03.2008 Luas264.155 HaJumlah penduduk5582Kepadatan- Air terjun Cikondang Cikondang adalah desa di kecamatan Cibeber, Cianjur, Jawa Barat, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administrasi Pemerintahan, dan Pulau tahun 2021 (Indonesia) Peraturan Menteri Dalam Negeri Nomor 72 Tahun 20...

Politics of Kenya National Government Constitution History Human rights LGBT rights Executive President (list) William Ruto Deputy President Rigathi Gachagua Cabinet Prime Cabinet Secretary Musalia Mudavadi Attorney General Justin Muturi Director of Public Prosecutions Renson M. Ingonga Legislature National Assembly Speaker: Moses Wetangula List of members Constituencies Senate Speaker: Amason Kingi List of members Judiciary Chief Justice Martha Koome Deputy Chief Justice Philomena Mwilu Supr...

العلاقات الأذربيجانية الرومانية أذربيجان رومانيا أذربيجان رومانيا تعديل مصدري - تعديل العلاقات الأذربيجانية الرومانية هي العلاقات الثنائية التي تجمع بين أذربيجان ورومانيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتي

2004 American filmSniper 3Official DVD coverDirected byP.J. PesceWritten by J.S. Cardone Ross Helford Based onCharactersby Michael Frost BecknerCrash LeylandProduced by Carol Kottenbrook Scott Einbinder Starring Tom Berenger Byron Mann Denis Arndt John Doman CinematographyMichael BonvillainEdited byAmanda I. KirpaulMusic byTim JonesProductioncompanies Sandstorm Films Destination Films Distributed byColumbia TriStar Home EntertainmentRelease date September 28, 2004 (2004-09-28) ...

Веселе Країна Україна УкраїнаАдмінодиниця Грем'яцька сільська радаЧасовий пояс UTC+2Телефонний код 4658 (Грем'яцька сільська рада) У Вікіпедії є статті про інші значення цього терміна: Веселе. Веселе — колишнє село в Україні, Новгород-Сіверському районі Черніг...

Халчайцький ВіталійЗагальна інформаціяНародження 22 серпня 1964 (59 років)(19640822)СпортВид спорту водне поло Участь і здобутки Віталій Халчайцький (нар. 22 серпня 1964) — український гравець у водне поло. Він брав участь у турнірі серед чоловіків на літніх Олімпійських і�...

Euroregion in Western Europe SaarLorLuxSaar–Lor–LuxSarLorLux Emblem Location and extent of the Greater Region of SaarLorLux in western Europe.TypeEuroregionMembership Saarland Lorraine Moselle Meurthe-et-Moselle Luxembourg Wallonia Communauté française Deutschsprachige Gemeinschaft Rhineland-Palatinate Establishment16 October 1980Area• Total65,400 km2 (25,300 sq mi)Population• 2019 estimate11,639,225• Density173/km2 (448.1/sq mi)CurrencyEuro (EUR...

British-bred Thoroughbred racehorse Harbour LawRacing silks of Jackie CornwellSireLawmanGrandsireInvincible SpiritDamAbunaiDamsirePivotalSexStallionFoaled30 March 2013[1]CountryIrelandColourBayBreederHascombe and Valiant StudsOwnerJackie Cornwell, Daniel Danny LeeTrainerJo CrowleyLaura MonganRecord8: 3-2-1Earnings£474,481Major winsSt Leger Stakes (2016) Harbour Law (foaled 30 March 2013) is a British Thoroughbred racehorse. Unraced as a two-year-old he showed steady improvement in 20...

SMA Negeri 1 BukittinggiInformasiDidirikan23 Juli 1959JenisNegeriAkreditasiA[1]Nomor Pokok Sekolah Nasional10307523[2]Kepala SekolahDra. Silfa Dusun, M.PdJumlah kelas33 kelasJurusan atau peminatanMIA dan IISRentang kelasX MIA, X IIS; XI MIA, XI IIS; XII MIA, XII IISKurikulumKurikulum 2013StatusDiakuiAlamatLokasiJl. Syekh M. Jamil Jambek No. 36, Bukittinggi, Sumatera Barat, IndonesiaTel./Faks.+62752 22549 - 626202Situs webwww.sman1bukittinggi.sch.idMoto SMA Neger...

2022 studio album by A Wilhelm ScreamLose Your DelusionStudio album by A Wilhelm ScreamReleasedApril 14, 2022StudioAnchor End Studio (Trevor Reilly's home studio in New Bedford, Massachusetts)GenreMelodic hardcore, thrash metalLength33:59LabelCreator-Destructor RecordsProducerTrevor Reilly, James WhittenA Wilhelm Scream chronology Partycrasher(2013) Lose Your Delusion(2022) Lose Your Delusion is the seventh overall studio album by Massachusetts-based melodic hardcore band A Wilhelm Sc...
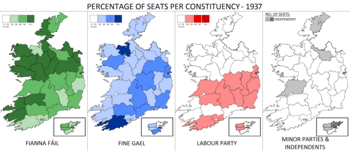
Election to the 9th Dáil 1937 Irish general election ← 1933 1 July 1937 1938 → ← outgoing memberselected members →138 seats in Dáil Éireann[a]70 seats needed for a majorityTurnout76.2% 5.1pp First party Second party Third party Leader Éamon de Valera W. T. Cosgrave William Norton Party Fianna Fáil Fine Gael Labour Leader since 26 March 1926 September 1934 19 July 1932 Leader's seat Clare Cork Borough Carlow�...

Geographical area within a city that is inhabited or frequented by LGBT people Gayborhood redirects here. For the area in Philadelphia, see Washington Square West, Philadelphia § The Gayborhood. The original Rainbow Crossing in Sydney's Surry Hills neighbourhood The Stonewall Inn in the gay village of Greenwich Village, New York City, the cradle of the modern gay rights movement[1][2][3] Part of a series onLGBT topics LesbianGa...

Railway station in Karnataka, India Yelahanka JunctionYalahaṅka JaṅkṣanYelahanka Jankshan Indian Railways stationGeneral informationLocationYelahanka Bangalore, KarnatakaIndiaCoordinates13°01′N 77°33′E / 13.02°N 77.55°E / 13.02; 77.55Elevation915.009 metres (3,002.00 ft)Owned byIndian RailwaysLine(s)Quadruple Electric LinePlatforms5Tracks5ConnectionsTaxiConstructionStructure typeAt GradePlatform levels1ParkingYesOther informationStatusActiveStation c...

This parking sign in San Francisco stipulates that motorists may only park for up to two hours from 8 a.m. to 9 p.m. Monday through Saturday unless the applicable residential parking permit is displayed Residential zoned parking is a local government practice of designating certain on-street automobile parking spaces for the exclusive use of nearby residents. It is a tool for addressing overspill parking from neighboring population centers (such as a shopping center, office building, apartmen...

Олександр Отрєп'єв Старший матрос Загальна інформаціяНародження 28 липня 1992(1992-07-28)Приют, Єланецький район, Миколаївська обл., УкраїнаСмерть 21 січня 2021(2021-01-21) (28 років)Гнутове, Сартанська селищна громада, Маріупольський район, Донецька область, Україна(вогнепальне пора...

Painting by the Dutch painter Jan Steen You can help expand this article with text translated from the corresponding article in Dutch. (January 2023) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not transl...
















