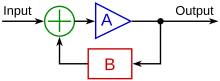
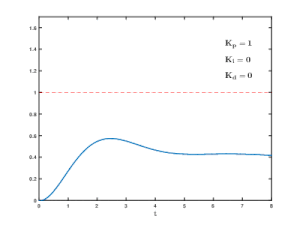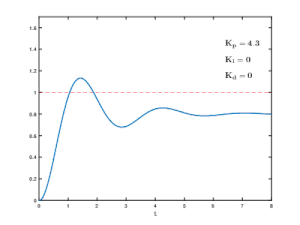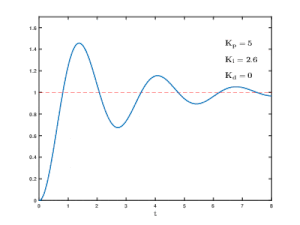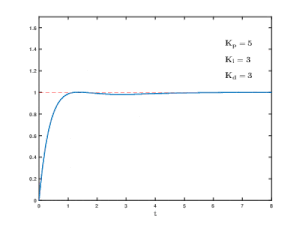
控制系統
|
Read other articles:

Like a VirginAlbum studio karya MadonnaDirilis12 November 19845 Agustus 1985 (Re-release)21 May 2001 (Remastered)DirekamApril - September 1984 di Power Station Studios, Manhattan, New York[1]GenreDance-Pop[2]Durasi43:10LabelSire Records, Warner Bros. Warner Bros. (2001)ProduserMadonna, Nile Rodgers, Stephen BrayKronologi Madonna Madonna(1983)Madonna1983 Like a Virgin(1984) True Blue(1986)True Blue1986 Like a Virgin adalah album kedua penyanyi pop Amerika Serikat Madonna, y...

Questa voce sull'argomento allenatori di calcio turchi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Mustafa Reşit Akçay Nazionalità Turchia Calcio Ruolo Allenatore Squadra Esenler Erokspor Carriera Carriera da allenatore 2001-2002 1926 Bulancakspor2003-2004 Gümüşhanespor2004-2005 Pazarspor2006-2007 Arsinspor2007-2008 Ofspor2008-2009 Beylerbeyi2009 ...

Wim Peters Wim Peters Algemene informatie Volledige naam Willem Marie Adriaan (Wim) Peters Geboren Oosterhout, 28 september 1921 Overleden Amersfoort, 23 februari 2019 Partij KVP Portaal Politiek Nederland Willem Marie Adriaan (Wim) Peters (Oosterhout, 28 september 1921 - Amersfoort, 23 februari 2019) was een Nederlands burgemeester van Wijk bij Duurstede, Cothen en Losser. Hij was tevens lid van de Provinciale Staten van Utrecht. In 1986 werd Peters benoemd tot officier in ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2020) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها...

Pour les articles homonymes, voir Église Notre-Dame-de-l'Assomption. Ne doit pas être confondu avec Église Notre-Dame-du-Châtel. Église Notre-Dame-de-l'Assomption La Terrasse donnant sur l'église. Présentation Culte Catholicisme romain Type Chapelle puis église Rattachement Diocèse d'Autun, Chalon et Mâcon Début de la construction 1757 Fin des travaux 1763 Architecte Jean-Baptiste Caristie Style dominant Art jésuite Nombre de flèches 1 Protection Classé MH (1943) Géo...

Kaisar Meksiko Bekas Kerajaan Imperial Lambang kerajaan Maximilian I Penguasa pertama Agustín I Penguasa terakhir Maximilian I Gelar His Imperial Majesty Pendirian 19 Mei 182210 April 1864 Pembubaran 19 Maret 182315 Mei 1867 Penuntut takhta Maximilian von Götzen-Itúrbide Kaisar Meksiko (bahasa Spanyol: Emperador de Meksiko) adalah kepala negara dan penguasa Meksiko pada dua periode yang tidak berurutan pada abad ke-19. Dengan Deklarasi Kemerdekaan Kekaisaran Meksiko dari Spanyol pada tahun...

Región de MbeyaMkoa wa Mbeya Región Coordenadas 8°30′S 33°00′E / -8.5, 33Capital MbeyaEntidad Región • País TanzaniaComisionado Abbas KandoroSuperficie • Total 62420 km²Población (2012) • Total 2 707 410 hab. • Densidad 43,37 hab/km² Sitio web oficial [editar datos en Wikidata] Mbeya es una de las veintiséis regiones administrativas en las que se encuentra dividida la República Unida d...

Zgromadzenie Sióstr Służebniczek Niepokalanego Poczęcia Najświętszej Maryi Panny Dewiza: Przez Maryję do Jezusa Pełna nazwa Zgromadzenie Sióstr Służebniczek NMP Niepokalanie Poczętej Nazwa łacińska Congregatio Sororum Servularum Beatae Mariae Virginis Immaculatae Conceptae Skrót zakonny ABMV Wyznanie katolickie Kościół rzymskokatolicki Założyciel bł. Edmund Bojanowski Data założenia 3 maja 1850 Strona internetowa Groby sióstr pionierek w Jaszkowie Budynek Zgromadzenia ...

Fictional character from the Disney's 2010 animated film Tangled Fictional character RapunzelTangled characterRapunzel as she appears in Tangled (2010).First appearanceTangled (2010)Based onRapunzelby the Brothers GrimmAdapted byGlen KeaneVoiced by Mandy MooreDelaney Rose Stein (young)(Tangled) Ivy George (young)(Tangled: The Series) Kelsey Lansdowne (Kingdom Hearts III)[1] Portrayed byElisha Ainsley(Tangled: The Musical)In-universe informationTitlePrincess of CoronaAffiliationDisney ...

2007 FIFA Women's World Cup2007年女子世界杯足球赛2007 Nián nǚzǐ shìjièbēi zúqiú sàiTournament detailsHost countryChinaDates10–30 SeptemberTeams16 (from 6 confederations)Venue(s)5 (in 5 host cities)Final positionsChampions Germany (2nd title)Runners-up BrazilThird place United StatesFourth place NorwayTournament statisticsMatches played32Goals scored111 (3.47 per match)Attendance1,190,971 (37,218 per match)Top scorer(s) Marta (7 ...

Poster for the 1938 New York production of One-Third of a Nation One Third of a Nation is a Living Newspaper play produced by the Federal Theatre Project in 1938. Written by Arthur Arent from research by the editorial staff of the Federal Theatre Project, it focused on the problem of housing in the United States and the growth of slums in New York City. The play was produced in New York and in nine additional cities, where it was adapted to specific community conditions. It was adapted as a f...

Indian television show MTV WebbedGenreTeen dramaCreated byVikas GuptaDirected bySaurabh AroraPresented byKritika KamraCountry of originIndiaOriginal languageHindiNo. of seasons2No. of episodes37ProductionProducersEkta KapoorShobha KapoorProduction locationIndiaCamera setupMulti-cameraRunning timeApprox. 22 minutesProduction companyBalaji TelefilmsOriginal releaseNetworkMTV IndiaReleaseSeptember 14, 2013 (2013-09-14) –September 21, 2014 (2014-09-21) MTV Webbed is an Indian tee...

Trichoferus pallidus Trichoferus pallidus Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Trichoferus Spesies: Trichoferus pallidus Trichoferus pallidus adalah spesies kumbang tanduk panjang yang tergolong famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Trichoferus, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu dan dapat menyebabkan ...

2003 video gameThe Temple of Elemental EvilDeveloper(s)Troika GamesPublisher(s)AtariDirector(s)Tim CainProducer(s)Thomas R. Decker Todd HartwigDesigner(s)Tim Cain Thomas R. DeckerProgrammer(s)Steve MoretArtist(s)Michael McCarthyComposer(s)Ron FishSeriesGreyhawkPlatform(s)WindowsReleaseNA: September 16, 2003[1]EU: October 10, 2003[2]Genre(s)Role-playing,[1] turn-based tactics[3]Mode(s)Single-player[1] The Temple of Elemental Evil is a 2003 role-playing v...

Turkish footballer Sezer Özmen Özmen with Çaykur Rizespor in September 2013Personal informationDate of birth (1992-07-07) 7 July 1992 (age 31)Place of birth Bakırköy, İstanbul, TurkeyHeight 1.89 m (6 ft 2 in)Position(s) DefenderTeam informationCurrent team FethiyesporNumber 92Youth career2005–2006 Bakırköyspor2006–2010 BeşiktaşSenior career*Years Team Apps (Gls)2010–2012 Beşiktaş 0 (0)2010–2012 → Çaykur Rizespor (loan) 44 (2)2012–2015 Çaykur Rizes...

Bylot Island Migratory Bird SanctuaryIUCN category II (national park)LocationSouthampton Island, Kivalliq, Nunavut, CanadaNearest townPond InletCoordinates73°14′58″N 78°35′15″W / 73.24944°N 78.58750°W / 73.24944; -78.58750Area12,635 km2 (4,878 sq mi)Established1965 The Bylot Island Migratory Bird Sanctuary is a migratory bird sanctuary in Qikiqtaaluk, Nunavut, Canada. Located on Bylot Island, it was federally designated in 1965, and is c...

مستشفى أريحا الحكومي الجديد إحداثيات 31°50′10″N 35°27′28″E / 31.8361299°N 35.4576415°E / 31.8361299; 35.4576415 معلومات عامة القرية أو المدينة أريحا الدولة فلسطين سنة التأسيس 1998 المالك وزارة الصحة الفلسطينية خدمات المستشفى التخصص مستشفى عام عدد الأسرّة 54 سرير معلومات أخرى تعدي�...

Village in Korçë, AlbaniaPanaritVillagePanaritCoordinates: 40°29′4″N 20°28′24″E / 40.48444°N 20.47333°E / 40.48444; 20.47333Country AlbaniaCountyKorçëMunicipalityKorçëMunicipal unitVithkuqTime zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST) Panarit (Albanian definite form: Panariti) is a community in the Korçë County, southeastern Albania which became part of the municipality Korçë[1] during the 2015 local government reform. No...

Japanese politician Michiharu Mishima三島 通陽Born(1897-01-01)January 1, 1897Azabu, Tōkyō, JapanDiedApril 20, 1965(1965-04-20) (aged 68)NationalityJapaneseOther namesShōdō Mishima (pen name)Occupation(s)Novelist, playwright, drama criticKnown forCo-founder of the Boy Scouts of Japan Scouting portal Viscount Michiharu Mishima (三島 通陽, Mishima Michiharu, January 1, 1897 – April 20, 1965) was a novelist, playwright and drama critic. His pen name was Shōdō Mi...

Hindu goddess, described as the mother of snakes SurasaMother of SnakesHanuman flies into the mouth of Surasa. From the mural of the Temple of the Emerald Buddha, Bangkok, Thailand.TextsRamayanaPersonal informationParentsDakshaSpouseKashyapa Surasa also Siras is a Hindu goddess, who is described as the mother of the nagas (serpents).[1] Her most popular tale appears in the Hindu epic Ramayana, where she is tasked to test the god Hanuman on his way to Lanka. Birth and children Hanuman ...