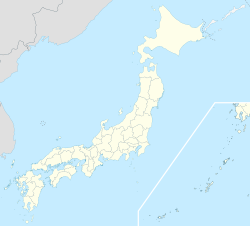
垂水市
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

ServampSampul manga volume pertama berbahasa InggrisSERVAMP -サーヴァンプ-(Sāvanpu)GenreSupernatural MangaPengarangStrike TanakaPenerbitMedia FactoryPenerbit bahasa InggrisNA Seven Seas EntertainmentMajalahMonthly Comic GeneDemografiShōjoTerbit15 Juni 2011 – sekarangVolume20 Seri animeSutradaraShigeyuki Miya[a]Hideaki NakanoSkenarioKenji KonutaMusikKenji KawaiStudioBrain's BasePlatinum VisionPelisensiNA FunimationSA/SEA Muse CommunicationSaluranasliAT-X, Tokyo MX, Sun TV, M�...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Maio de 2023) Ajude a melhorar este artigo sobre Arquitetura ilustrando-o com uma imagem. Consulte Política de imagens e Como usar imagens. A Igreja de Nossa Senhora da Assunção apresenta-se como a igreja matriz de Gralhas situada na fr...

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pe...

Wer nur den lieben Gott läßt waltenBWV 93Chorale cantata by Johann Sebastian BachGeorg Neumark, author of the hymnOccasionFifth Sunday after TrinityChoraleWer nur den lieben Gott läßt waltenPerformed9 July 1724 (1724-07-09): LeipzigMovementssevenVocalSATB choir and soloInstrumental2 oboes2 violinsviolaviola da gambacontinuo Johann Sebastian Bach composed the church cantata Wer nur den lieben Gott läßt walten (Who only lets dear God rule),[1] BWV 93 in Leipzig...

Collective term for the sepals and petals, or either of them if one is absent A mature flower. In this example the perianth is separated into a calyx (sepals) and corolla (petals) The perianth (perigonium, perigon or perigone in monocots) is the non-reproductive part of the flower, and structure that forms an envelope surrounding the sexual organs, consisting of the calyx (sepals) and the corolla (petals) or tepals when called a perigone. The term perianth is derived from Greek περί (peri...

Indian film festival The logo of Tigerland India Film Festival; all four primary colours in one logo symbolise the need for contribution of everyone for the success of conservation of our natural wealth Tigerland India Film Festival (TIFF) is an environmental and wildlife film festival based in India. Waheeda Rehman at the exhibition of her wildlife photographs organised under TIFF 2015 It is organized by a non-profit organization 'Society for Tigerland Conservation' and the aim of the festiv...

New Zealand rugby league footballer Charlie HerekotukutukuHerekotukutuku playing for North SydneyPersonal informationBornNew ZealandHeight1.76 m (5 ft 9+1⁄2 in)Weight83 kg (13 st 1 lb)Playing informationPositionFullback, Five-eighth, Halfback Representative Years Team Pld T G FG P 2004 New Zealand Māori 3 0 0 0 0 As of 23 February 2010 Charlie Herekotukutuku (birth unknown) is a New Zealand rugby league footballer who currently plays for the Balmai...

Kenyan-American runner Bernard LagatLagat in 2011Personal informationFull nameBernard Kipchirchir LagatNationalityKenyan-AmericanBornDecember 12, 1974 (1974-12-12) (age 48)Kapsabet, KenyaHeight175 cm (5 ft 9 in)[1]Weight59 kg (130 lb)[1]SportCountry United States KenyaSportAthletics/Track, Long-distance runningEvent800 m – MarathonCollege teamWashington State CougarsClubNikeTurned pro1998Coached byJames LiAchievements and ti...

Federação Togolesa de Futebol Fundação 1960 Filiação à FIFA em 1962 Filiação à CAF em 1963 Presidente Gabriel Komla Kuma Mawulawoè Seleção Seleção Togolesa de Futebol A Federação Togolesa de Futebol (em francês: Fédération Togolaise de Football, FTF) é uma associação de clubes de futebol de Togo e organiza jogos internacionais e nacionais para a Seleção do Togo. A Federação Nacional do Togo foi fundada em 1960. É afiliada a FIFA desde 1962 e é um membro da CAF des...

906th Fighter Group F-16s of the 906th Fighter Group at Wright-Patterson AFB[note 1]Active1962-1975; 1982-1994Country United StatesBranch United States Air ForceRoleFighterInsignia906th Tactical Fighter Group emblem (approved 1983)Military unit The 906th Fighter Group is an inactive United States Air Force Reserve unit. It was last active with the 445th Airlift Wing, at Wright-Patterson Air Force Base, Ohio, where it was inactivated on 1 October 1994. History Need for reserv...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (December 2020) (Learn how and when to remove this template message) This article needs additional citations for verification. Please help improve thi...

Професор Крамаренко Василь Пилипович у товаристві випускників Львівського державного медичного інституту 1962 року. Зміст: Top · А· Б· В· Г· Ґ· Д· Е· Є· Ж· З· И· І· Ї· Й· К· Л· М· Н· О· П· Р· С· Т· У· Ф· Х· Ц· Ч· Ш· Щ· Ю· Я Це список випускників Львівського медичного інституту ім...

جورج آر. سويفت (بالإنجليزية: George R. Swift) معلومات شخصية الميلاد 19 ديسمبر 1887 مقاطعة بالدوين الوفاة 10 سبتمبر 1972 (84 سنة) نيو أورلينز مواطنة الولايات المتحدة مناصب عضو مجلس الشيوخ الأمريكي[1] عضو خلال الفترة15 يونيو 1946 – 5 نوفمبر 1946 فترة برلمان...

SMA Negeri 10 SurabayaInformasiDidirikan10 April 1977JenisSekolah NegeriAkreditasiA[1]Nomor Statistik Sekolah301056012010Nomor Pokok Sekolah Nasional20532243MaskotOctodistJumlah kelas33 Ruang KelasJurusan atau peminatanIPA dan IPSRentang kelasX MIPA dan X IPS XI MIPA dan XI IPS XII MIPA dan XII IPSKurikulumKurikulum 2013AlamatLokasiJl. Jemursari I No. 28, Surabaya, Jawa Timur, IndonesiaTel./Faks.(031) 8415273Situs websma10surabaya.sch.idLain-lainLulusanSatria Tama Hard...

司替戊醇臨床資料读音stiri pen' tol 商品名(英语:Drug nomenclature)DiacomitAHFS/Drugs.comMonographMedlinePlusa618069核准狀況 歐 EMA: yes 美 DailyMed: Stiripentol 懷孕分級 澳: B3 给药途径By mouthATC碼N03AX17 (WHO) 法律規範狀態法律規範 澳:限医生处方(S4) 加:处方药(℞-only) 歐:[3] 英:处方药(℞-only) (POM)[1] 美:处方药(℞-only)[2] 处方...

Sexual fetish involving dolls Two women posing as latex dolls. Doll fetishism is a sexual fetish in which an individual is attracted to dolls and doll like objects such as figurines.[1] The attraction may include the desire for actual sexual contact with a doll, a fantasy of a sexual encounter with an animate or inanimate doll, encounters between dolls themselves, or sexual pleasure gained from thoughts of being transformed or transforming another into a doll. Doll fetishism is a form...

Cemetery in Estonia You can help expand this article with text translated from the corresponding article in Estonian. (August 2023) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appe...

American politician Lee JamesMember of the Pennsylvania House of Representativesfrom the 64th districtIncumbentAssumed office January 1, 2013[1]Preceded byScott Hutchinson Personal detailsBornRobert Lee James (1948-11-20) November 20, 1948 (age 75)Political partyRepublicanResidenceCranberry Township, Venango County, PennsylvaniaAlma materClarion UniversityOccupationinvestment manager Robert Lee James (born November 20, 1948) is a Republican member of the Pennsylva...

Albert Pahimi Padackéألبر بهيمي بدكي Perdana Menteri ChadMasa jabatan26 April 2021 – 12 Oktober 2022PresidenMahamat Déby PendahuluPosisi dibentuk kembaliPenggantiSaleh KebzaboMasa jabatan15 Februari 2016 – 4 Mei 2018PresidenIdriss Déby PendahuluKalzeubet Pahimi DeubetPenggantiPosisi dihapus Informasi pribadiLahir15 November 1966 (umur 57)Gouin, Persekutuan Afrika Prancis Khatulistiwa (sekarang Chad)Partai politikReli Nasional untuk DemokrasiAlma mate...

Demostración visual del teorema de la probabilidad total para el caso n = 4. El teorema de la probabilidad total afirma lo siguiente: Sea A 1 , A 2 , . . . , A n {\displaystyle A_{1},A_{2},...,A_{n}} una partición sobre el espacio muestral y sea B {\displaystyle B} un suceso cualquiera del que se conocen las probabilidades condicionales P ( B | A i ) {\displaystyle P(B|A_{i})} , entonces la probabilidad del suceso B {\displaystyle B} viene dada por la expresión: P ( B ) = ∑ i = 1 n ...