Hạt điểm
|
Read other articles:

National ministry of financeMinistry of FinanceKementerian Kewangan(MOF)Coat of arms of MalaysiaMinistry overviewFormed31 August 1957; 66 years ago (1957-08-31)JurisdictionGovernment of MalaysiaHeadquartersMinistry of Finance Complex, No. 5, Persiaran Perdana, Precinct 2, Federal Government Administrative Centre, 62592 PutrajayaEmployees30,735 (2022)Annual budgetMYR 45,990,876,000 (2022)Minister responsibleAnwar Ibrahim, Minister of FinanceDeputy Minister responsibleAhmad Ma...

Melacacidin Nombre IUPAC (2R,3R,4R)-2-(3,4-dihydroxyphenyl)-3,4-dihydro-2H-chromene-3,4,7,8-tetrolGeneralFórmula estructural Fórmula molecular ?IdentificadoresNúmero CAS 38081-16-2[1]ChemSpider 148659PubChem 169996 SMILESC1=CC(=C(C=C1C2C(C(C3=C(O2)C(=C(C=C3)O)O)O)O)O)O InChIInChI=InChI=1S/C15H14O7/c16-8-3-1-6(5-10(8)18)14-13(21)11(19)7-2-4-9(17)12(20)15(7)22-14/h1-5,11,13-14,16-21H/t11-,13-,14-/m1/s1Key: JEUXGAUBSWADEA-MRVWCRGKSA-N Propiedades físicasMasa molar 306,26 g/m...

Hafner Rotachute Typ Experimentalflugzeug, Tragschrauber Entwurfsland Vereinigtes Konigreich Vereinigtes Königreich Hersteller F. Hills & Son Erstflug 11. Februar 1942 (im Fahrzeugschlepp) Stückzahl etwa 8 P-5 im Museum of Army Flying Der Hafner Rotachute ist ein als Tragschrauber ausgelegtes experimentelles Fluggerät, das von Raoul Hafner konstruiert und von Hills & Son in Manchester gebaut wurde. Inhaltsverzeichnis 1 Geschichte 1.1 Entwicklung 1.2 Erprobung 1.3 Weitere Nutzu...

الهدار الجنوبي موقع محافظة الأفلاج بالنسبة لمنطقة الرياض تقسيم إداري البلد السعودية التقسيم الأعلى منطقة الرياض السكان التعداد السكاني غير معروف نسمة (إحصاء ) تعديل مصدري - تعديل الهدار الجنوبي، هي قرية من فئة (ب) تقع في محافظة الأفلاج[؟]، والتابعة لمنطقة الري

Koryolink고려링크JenisPerusahaan patunganIndustriTelekomunikasiDidirikan2008KantorpusatPyongyangWilayah operasiPyongyang, dan lima kota utama dan delapan jalan besar dan jalur kereta api.ProdukTelephony, GPRSPendapatanAS$ 5.8 million in the quarter, before accounting for interest payments, taxes, depreciation and amortization.IndukGlobal Telecom Holding Korea Posts and Telecommunications CorporationSitus webtidak ada Koryolink (bahasa Korea: 고려링크, disebut sebagai koryolink), s...

Hans-Joachim Uthke (2021) Hans-Joachim Uthke (* 23. Mai 1941 in Kalwe, im Landkreis Stuhm (Westpreußen)), heute Kalwa, Teil der Landgemeinde Stary Targ, ist ein deutscher Grafiker und Aphoristiker. Inhaltsverzeichnis 1 Leben 2 Werk 3 Preise und Auszeichnungen 4 Ausstellungen 5 Veröffentlichungen (Auswahl) 6 Literatur 7 Weblinks 8 Einzelnachweise Leben Hans-Joachim Uthke wuchs in Norddeutschland auf und studierte an der Famous Artist’s School bei Ben Nicholson.[1][2] Er nah...

Book by Phil Stong This article is about the original 1932 novel. For the later film and musical versions, see State Fair (1933 film), State Fair (1945 film), State Fair (1962 film), State Fair (1976 film), and State Fair (musical). State Fair Dust jacket art for 1932 first editionAuthorPhil StongCountryUnited StatesLanguageEnglishGenreRealistic fictionPublished1932 by Century Co. of PhiladelphiaISBN9780854681877 State Fair is a 1932 novel by Phil Stong about an Iowa farm family's visit to th...

Occupation of land or buildings without the permission of the relevant authorities South Korea on globe (dark green) Squatting in South Korea is the occupation of land or buildings without the permission of the relevant authorities. From the 1950s onwards, shanty towns called P'anjach'on formed around cities, in particular the capital Seoul. As well as providing housing, squatting is used as a tactic by groups opposing gentrification and striking workers. History At the end of the Korean War ...

2005 single by Snoop Dogg and Daddy Yankee Gangsta ZoneSingle by Daddy Yankee featuring Snoop Doggfrom the album Barrio Fino en Directo Released2005GenreReggaetonhardcore hip hopLength3:33LabelInterscopeEl CartelSongwriter(s)Ramón AyalaCalvin BroadusProducer(s)Nely[1]NaldoDaddy Yankee singles chronology Rompe(2005) Gangsta Zone(2005) Machucando(2005) Snoop Dogg singles chronology Real Soon(2005) Gangsta Zone(2005) Say Somethin'(2006) Gangsta Zone is a song by rappers Daddy Ya...

French film director Jean VigoVigo, 1930sBorn(1905-04-26)26 April 1905Paris, FranceDied5 October 1934(1934-10-05) (aged 29)Paris, FranceOccupationFilm directorYears active1930–1934 Jean Vigo (French: [vigo]; 26 April 1905 – 5 October 1934) was a French film director who helped establish poetic realism in film in the 1930s. His work influenced French New Wave cinema of the late 1950s and early 1960s. Biography Vigo was born to Emily Clero and the militant anarchist Mi...

Love Island GamesGenreRealityPresented by Maya Jama Ariana Madix Maura Higgins Narrated byIain StirlingOriginal languageEnglishNo. of series1No. of episodes19Original releaseNetworkPeacockRelease1 November (2023-11-01) –20 November 2023 (2023-11-20)RelatedLove Island franchise Love Island Games is a spin-off of the reality dating series Love Island. It features previous Love Island contestants from various countries in the franchise competing in challenges. The show premiered...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dance Premier League – news · newspapers · books · scholar · JSTOR (September 2019) (Learn how and when to remove this template message) Indian TV series or programme Dance Premier LeagueTitle cardGenreDance reality showPresented byHussain Kuwajerwala,Eija...

2013 film by Uğur Yücel Benim DünyamFilm posterDirected byUğur YücelWritten byUgras Günes, Can YücelProduced byErol AvciStarringBeren Saat Uğur YücelRelease date 25 October 2013 (2013-10-25) Running time100 minutesCountryTurkeyLanguageTurkish Benim Dünyam (My World) is a 2013 Turkish drama film directed by Uğur Yücel.[1] It is the remake of the 2005 Indian film, Black[2] which in turn was inspired by the true story of American political activist and ...

أشاويخ تقسيم إداري البلد المغرب الجهة بني ملال خنيفرة الإقليم أزيلال الدائرة ولتانة الجماعة القروية آيت بلال المشيخة آيت بلال السكان التعداد السكاني 169 نسمة (إحصاء 2004) • عدد الأسر 21 معلومات أخرى التوقيت ت ع م±00:00 (توقيت قياسي)[1]، وت ع م+01:00 (توقيت صيفي)[1] ...

Veve Zulfikar BasyaibanZulfikar performing in 2019BornVeryal Eisha Aqila (2003-07-07) 7 July 2003 (age 20)Jombang Regency, East Java, IndonesiaNationalityIndonesianOther namesVeve ZulfikarOccupations Singer qāriʾah brand ambassador actress YouTuber OrganizationNahdlatul Ulama[1]Parents Zulfikar Mohammad Basyaiban (father) Riza Fitriya Zahro (mother) Relatives Zara Zulfikar Basyaiban (younger sister) Haidar Zulfikar Basyaiban (younger brother) Maira Zulfikar Basyaiban (youn...

Defunct family-owned company headquartered in Los Angeles, California National Stores Inc.TypePrivateTraded asFallas Discount StoresIndustryRetailFoundedLos Angeles, California, 1962FounderJoseph FallasDefunct2022HeadquartersHarbor Gateway, Los Angeles, CaliforniaNumber of locations2Area servedUnited States, Puerto RicoProductsbrand name clothing, private label clothing, shoes, household itemsOwnerMichael FallasNumber of employees≈2,200Websitewww.fallasstores.net National Stores Inc., was a...
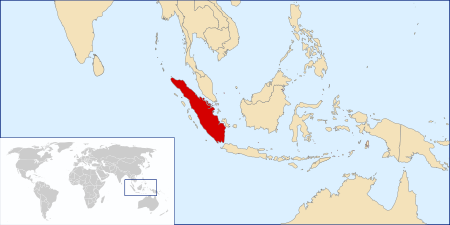
Pulau pulau kecil di sekitar pulau sumatra: Aceh Pulau Babi Pulau Bangkaru Pulau gajah Pulau Kayee Pulau Lasia Pulau Nasi Pulau Benggala Pulau Panyang Pulau Pasi Pulau Peunasue Pulau Penasi Pulau Raya Pulau Reusam Pulau Rondo Pulau Rusa Pulau Salaut Besar Pulau Sembilan Pulau Seumut Pulau Simeulue Pulau Simeuleu ceut Pulau Tapah Pulau Trumon Pulau Tuangku Pulau Tulo Pulau Weh Sumatera Utara Pulau Bojo Kepulauan Hinako Pulau Musala Pulau Nias Pulau Pangururan Pulau Pini Pulau Tanabala Pulau Ta...

Duchess of Braganza Adelaide of Löwenstein-Wertheim-RosenbergBorn(1831-04-03)3 April 1831Kleinheubach, Kingdom of Bavaria, German ConfederationDied16 December 1909(1909-12-16) (aged 78)Ryde, Isle of Wight, United KingdomBurialPantheon of the Braganças, Lisbon, PortugalSpouse Miguel I of Portugal (m. 1851; died 1866)Issue Infanta Maria das Neves, Duchess of San Jaime Prince Miguel, Duke of Braganza Maria Teresa, Archduchess of Austria ...

1983 studio album by Cee FarrowRed and BlueStudio album by Cee FarrowReleased1983GenreNew wave, synthpopLength38:35LabelRocshire RecordsProducerAndy Lunn Red and Blue is the debut and only album from German singer Cee Farrow, released in 1983. Background Originally a model, Farrow signed to Rocshire Records to release a full studio album. He worked with producer Andy Lunn and co-wrote various tracks, mainly with German keyboardist Lothar Krell.[1] Red and Blue was recorded at ...

Pramuka Siaga di Jakenan, Pati sedang mengikuti kegiatan Siaga adalah sebutan bagi anggota Pramuka yang berumur antara 7–10 tahun. Disebut pramuka siaga karena sesuai dengan kiasan (kiasan dasar) masa perjuangan bangsa Indonesia, yaitu ketika rakyat Indonesia menyiagakan dirinya untuk mencapai kemerdekaan dengan berdirinya Boedi Oetomo pada tahun 1908 sebagai tonggak awal perjuangan bangsa Indonesia. Kode kehormatan Kode kehormatan bagi pramuka siaga ada dua, yaitu Dwi Satya (janji pramuka ...