–§—Г–љ–Ї—Ж—Ц—П –і—Ц–ї—М–љ–Є–Ї—Ц–≤
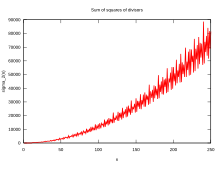
–§—Г–љ–Ї—Ж—Ц—П –і—Ц–ї—М–љ–Є–Ї—Ц–≤ ѕГ0 (n ) –і–Њ n = 250 –°–Є–≥–Љ–∞-—Д—Г–љ–Ї—Ж—Ц—П ѕГ1 (n ) –і–Њ n = 250 —Б—Г–Љ–∞ –Ї–≤–∞–і—А–∞—В—Ц–≤ –і—Ц–ї—М–љ–Є–Ї—Ц–≤, ѕГ2 (n ), –і–Њ n = 250 –§—Г–љ–Ї—Ж—Ц—П –і—Ц–ї—М–љ–Є–Ї—Ц–≤ вАФ –∞—А–Є—Д–Љ–µ—В–Є—З–љ–∞ —Д—Г–љ–Ї—Ж—Ц—П , –њ–Њ–≤'—П–Ј–∞–љ–∞ –Ј –і—Ц–ї—М–љ–Є–Ї–∞–Љ–Є —Ж—Ц–ї–Њ–≥–Њ —З–Є—Б–ї–∞ . –§—Г–љ–Ї—Ж—Ц—П –≤—Ц–і–Њ–Љ–∞ —В–∞–Ї–Њ–ґ –њ—Ц–і –љ–∞–Ј–≤–Њ—О —Д—Г–љ–Ї—Ж—Ц—П –і–Є–≤—Ц–Ј–Њ—А—Ц–≤ . –Ч–∞—Б—В–Њ—Б–Њ–≤—Г—Ф—В—М—Б—П, –Ј–Њ–Ї—А–µ–Љ–∞, –њ—А–Є –і–Њ—Б–ї—Ц–і–ґ–µ–љ–љ—Ц –Ј–≤'—П–Ј–Ї—Г –і–Ј–µ—В–∞-—Д—Г–љ–Ї—Ж—Ц—Ч –†—Ц–Љ–∞–љ–∞ —Ц —А—П–і—Ц–≤ –Х–є–Ј–µ–љ—И—В–µ–є–љ–∞ –і–ї—П –Љ–Њ–і—Г–ї—П—А–љ–Є—Е —Д–Њ—А–Љ . –Т–Є–≤—З–∞–ї–∞—Б—П –†–∞–Љ–∞–љ—Г–і–ґ–∞–љ–Њ–Љ , —П–Ї–Є–є –≤–Є–≤—Ц–≤ —А—П–і –≤–∞–ґ–ї–Є–≤–Є—Е —А—Ц–≤–љ–Њ—Б—В–µ–є –≤ –Љ–Њ–і—Г–ї—М–љ—Ц–є –∞—А–Є—Д–Љ–µ—В–Є—Ж—Ц —Ц –∞—А–Є—Д–Љ–µ—В–Є—З–љ–Є—Е —В–Њ—В–Њ–ґ–љ–Њ—Б—В–µ–є.
–Ч —Д—Г–љ–Ї—Ж—Ц—Ф—О –і—Ц–ї—М–љ–Є–Ї—Ц–≤ —В—Ц—Б–љ–Њ –њ–Њ–≤'—П–Ј–∞–љ–∞ —Б—Г–Љ–∞—В–Њ—А–љ–∞ —Д—Г–љ–Ї—Ж—Ц—П –і—Ц–ї—М–љ–Є–Ї—Ц–≤ , —П–Ї–∞, —П–Ї –≤–Є–њ–ї–Є–≤–∞—Ф –Ј –љ–∞–Ј–≤–Є, —Ф —Б—Г–Љ–Њ—О —Д—Г–љ–Ї—Ж—Ц—Ч –і—Ц–ї—М–љ–Є–Ї—Ц–≤.
–§—Г–љ–Ї—Ж—Ц—П —Б—Г–Љ–∞ –і–Њ–і–∞—В–љ–Є—Е –і—Ц–ї—М–љ–Є–Ї—Ц–≤ ѕГx n ) –і–ї—П –і—Ц–є—Б–љ–Њ–≥–Њ –∞–±–Њ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ–≥–Њ —З–Є—Б–ї–∞ x –≤–Є–Ј–љ–∞—З–∞—Ф—В—М—Б—П —П–Ї —Б—Г–Љ–∞ x —Б—В–µ–њ–µ–љ—Ц–≤ –і–Њ–і–∞—В–љ–Є—Е –і—Ц–ї—М–љ–Є–Ї—Ц–≤ —З–Є—Б–ї–∞ n . –§—Г–љ–Ї—Ж—Ц—О –Љ–Њ–ґ–љ–∞ –≤–Є—А–∞–Ј–Є—В–Є —Д–Њ—А–Љ—Г–ї–Њ—О
σ ѕГ -->
x
(
n
)
=
∑ вИС -->
d
|
n
d
x
,
{\displaystyle \sigma _{x}(n)=\sum _{d|n}d^{x}\,\!,}
–і–µ
d
|
n
{\displaystyle {d|n}}
d –і—Ц–ї–Є—В—М n ¬ї.
–Э–∞–є–≤–∞–ґ–ї–Є–≤—Ц—И–Є–Љ–Є —З–∞—Б—В–Ї–Њ–≤–Є–Љ–Є –≤–Є–њ–∞–і–Ї–∞–Љ–Є —Ф x = 0 —Ц x = 1. –Ф–ї—П –њ–Њ–Ј–љ–∞—З–µ–љ–љ—П ѕГ0 (n ) –∞–±–Њ —Д—Г–љ–Ї—Ж—Ц—Ч –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц –і—Ц–ї—М–љ–Є–Ї—Ц–≤ –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—В—М—Б—П —В–∞–Ї–Њ–ґ –њ–Њ–Ј–љ–∞—З–µ–љ–љ—П d (n ), ќљ(n ) –Є ѕД(n ) (–≤—Ц–і –љ—Ц–Љ–µ—Ж—М–Ї–Њ–≥–Њ Teiler = –і—Ц–ї—М–љ–Є–Ї) [ 1] [ 2] 0 (n ) = d (n ) –і–Њ—А—Ц–≤–љ—О—Ф –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц —В–Њ—З–Њ–Ї (x , y ) –Ј —Ж—Ц–ї–Є–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є —Г ¬Ђ–њ—А–∞–≤–Њ–Љ—Г –≤–µ—А—Е–љ—М–Њ–Љ—Г –Ї–≤–∞–і—А–∞–љ—В—Ц¬ї, —Й–Њ –ї–µ–ґ–∞—В—М –љ–∞ –≥—Ц–њ–µ—А–±–Њ–ї—Ц xy = n.
–ѓ–Ї—Й–Њ x –і–Њ—А—Ц–≤–љ—О—Ф 1, —Д—Г–љ–Ї—Ж—Ц—П –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —Б–Є–≥–Љ–∞-—Д—Г–љ–Ї—Ж—Ц—Ф—О –∞–±–Њ —Б—Г–Љ–Њ—О –і—Ц–ї—М–љ–Є–Ї—Ц–≤ [ 3] n ) —Ф –µ–Ї–≤—Ц–≤–∞–ї–µ–љ—В–љ–Є–Љ ѕГ1 (n ) [ 4]
–Я–Њ–≤'—П–Ј–∞–љ–Њ—О –Ј ѕГ(n ) —Ф —Д—Г–љ–Ї—Ж—Ц—П s (n ), —Й–Њ —Ф —А—Ц–≤–љ–Њ—О —Б—Г–Љ—Ц –≤–ї–∞—Б–љ–Є—Е –і—Ц–ї—М–љ–Є–Ї—Ц–≤ (—В–Њ–±—В–Њ –і—Ц–ї—М–љ–Є–Ї—Ц–≤, –Ј–∞ –≤–Є–љ—П—В–Ї–Њ–Љ —Б–∞–Љ–Њ–≥–Њ n ) [ 5] s (n ) = ѕГ1 (n ) - n .
–Э–∞–њ—А–Є–Ї–ї–∞–і, ѕГ0 (12) вАФ –Ї—Ц–ї—М–Ї—Ц—Б—В—М –і—Ц–ї—М–љ–Є–Ї—Ц–≤ —З–Є—Б–ї–∞ 12:
σ ѕГ -->
0
(
12
)
=
1
0
+
2
0
+
3
0
+
4
0
+
6
0
+
12
0
=
1
+
1
+
1
+
1
+
1
+
1
=
6
,
{\displaystyle {\begin{aligned}\sigma _{0}(12)&=1^{0}+2^{0}+3^{0}+4^{0}+6^{0}+12^{0}\\&=1+1+1+1+1+1=6,\end{aligned}}}
—В–Њ–і—Ц —П–Ї ѕГ1 (12) вАФ —Б—Г–Љ–∞ –≤—Б—Ц—Е –і—Ц–ї—М–љ–Є–Ї—Ц–≤:
σ ѕГ -->
1
(
12
)
=
1
1
+
2
1
+
3
1
+
4
1
+
6
1
+
12
1
=
1
+
2
+
3
+
4
+
6
+
12
=
28
,
{\displaystyle {\begin{aligned}\sigma _{1}(12)&=1^{1}+2^{1}+3^{1}+4^{1}+6^{1}+12^{1}\\&=1+2+3+4+6+12=28,\end{aligned}}}
—Ц —Б—Г–Љ–∞ s(12) –≤–ї–∞—Б–љ–Є—Е –і—Ц–ї—М–љ–Є–Ї—Ц–≤ —Ф —А—Ц–≤–љ–Њ—О:
s
(
12
)
=
1
1
+
2
1
+
3
1
+
4
1
+
6
1
=
1
+
2
+
3
+
4
+
6
=
16.
{\displaystyle {\begin{aligned}s(12)&=1^{1}+2^{1}+3^{1}+4^{1}+6^{1}\\&=1+2+3+4+6=16.\end{aligned}}}
n
–Ф—Ц–ї—М–љ–Є–Ї–Є
ѕГ0 (n )
ѕГ1 (n )
s (n ) = ѕГ1 (n ) вИТ n
–Ъ–Њ–Љ–µ–љ—В–∞—А—Ц
1
1
1
1
0
–Ї–≤–∞–і—А–∞—В: –Ј–љ–∞—З–µ–љ–љ—П ѕГ0 (n ) —Ф –љ–µ–њ–∞—А–љ–Є–Љ; —Б—В–µ–њ—Ц–љ—М 2: s(n ) = n вИТ 1 (–Љ–∞–є–ґ–µ –і–Њ—Б–Ї–Њ–љ–∞–ї–µ)
2
1,2
2
3
1
–њ—А–Њ—Б—В–µ: ѕГ1 (n) = 1+n, —В–∞–Ї —Й–Њ s(n) =1
3
1,3
2
4
1
–њ—А–Њ—Б—В–µ: ѕГ1 (n) = 1+n, —В–∞–Ї —Й–Њ s(n) =1
4
1,2,4
3
7
3
–Ї–≤–∞–і—А–∞—В: ѕГ0 (n ) —Ф –љ–µ–њ–∞—А–љ–Є–Љ; —Б—В–µ–њ—Ц–љ—М 2: s (n ) = n вИТ 1 (–Љ–∞–є–ґ–µ –і–Њ—Б–Ї–Њ–љ–∞–ї–µ)
5
1,5
2
6
1
–њ—А–Њ—Б—В–µ: ѕГ1 (n) = 1+n, —В–∞–Ї —Й–Њ s(n) =1
6
1,2,3,6
4
12
6
–њ–µ—А—И–µ –і–Њ—Б–Ї–Њ–љ–∞–ї–µ —З–Є—Б–ї–Њ : s (n ) = n
7
1,7
2
8
1
–њ—А–Њ—Б—В–µ: ѕГ1 (n) = 1+n, —В–∞–Ї —Й–Њ s(n) =1
8
1,2,4,8
4
15
7
—Б—В–µ–њ—Ц–љ—М 2: s (n ) = n - 1 (–Љ–∞–є–ґ–µ –і–Њ—Б–Ї–Њ–љ–∞–ї–µ)
9
1,3,9
3
13
4
–Ї–≤–∞–і—А–∞—В: ѕГ0 (n ) —Ф –љ–µ–њ–∞—А–љ–Є–Љ
10
1,2,5,10
4
18
8
11
1,11
2
12
1
–њ—А–Њ—Б—В–µ: ѕГ1 (n) = 1+n, —В–∞–Ї —Й–Њ s(n) =1
12
1,2,3,4,6,12
6
28
16
–њ–µ—А—И–µ –љ–∞–і–ї–Є—И–Ї–Њ–≤–µ —З–Є—Б–ї–Њ : s (n ) > n
13
1,13
2
14
1
–њ—А–Њ—Б—В–µ: ѕГ1 (n) = 1+n, —В–∞–Ї —Й–Њ s(n) =1
14
1,2,7,14
4
24
10
15
1,3,5,15
4
24
9
16
1,2,4,8,16
5
31
15
–Ї–≤–∞–і—А–∞—В: ѕГ0 (n ) —Ф –љ–µ–њ–∞—А–љ–Є–Љ; —Б—В–µ–њ—Ц–љ—М 2: s (n ) = n - 1 (–Љ–∞–є–ґ–µ –і–Њ—Б–Ї–Њ–љ–∞–ї–µ)
ѕГ0 (n )
+0
+1
+2
+3
+4
+5
+6
+7
+8
+9
+10
+11
0+
1
2
2
3
2
4
2
4
3
4
2
12+
6
2
4
4
5
2
6
2
6
4
4
2
24+
8
3
4
4
6
2
8
2
6
4
4
4
36+
9
2
4
4
8
2
8
2
6
6
4
2
48+
10
3
6
4
6
2
8
4
8
4
4
2
60+
12
2
4
6
7
4
8
2
6
4
8
2
72+
12
2
4
6
6
4
8
2
10
5
4
2
84+
12
4
4
4
8
2
12
4
6
4
4
4
96+
12
2
6
6
9
2
8
2
8
8
4
2
108+
12
2
8
4
10
2
8
4
6
6
4
4
120+
16
3
4
4
6
4
12
2
8
4
8
2
132+
12
4
4
8
8
2
8
2
12
4
4
4
ѕГ1 (n )
+0
+1
+2
+3
+4
+5
+6
+7
+8
+9
+10
+11
0+
1
3
4
7
6
12
8
15
13
18
12
12+
28
14
24
24
31
18
39
20
42
32
36
24
24+
60
31
42
40
56
30
72
32
63
48
54
48
36+
91
38
60
56
90
42
96
44
84
78
72
48
48+
124
57
93
72
98
54
120
72
120
80
90
60
60+
168
62
96
104
127
84
144
68
126
96
144
72
72+
195
74
114
124
140
96
168
80
186
121
126
84
84+
224
108
132
120
180
90
234
112
168
128
144
120
96+
252
98
171
156
217
102
216
104
210
192
162
108
108+
280
110
216
152
248
114
240
144
210
182
180
144
120+
360
133
186
168
224
156
312
128
255
176
252
132
132+
336
160
204
240
270
138
288
140
336
192
216
168
ѕГ2 (n )
+0
+1
+2
+3
+4
+5
+6
+7
+8
+9
+10
+11
0+
1
5
10
21
26
50
50
85
91
130
122
12+
210
170
250
260
341
290
455
362
546
500
610
530
24+
850
651
850
820
1050
842
1300
962
1365
1220
1450
1300
36+
1911
1370
1810
1700
2210
1682
2500
1850
2562
2366
2650
2210
48+
3410
2451
3255
2900
3570
2810
4100
3172
4250
3620
4210
3482
60+
5460
3722
4810
4550
5461
4420
6100
4490
6090
5300
6500
5042
72+
7735
5330
6850
6510
7602
6100
8500
6242
8866
7381
8410
6890
84+
10500
7540
9250
8420
10370
7922
11830
8500
11130
9620
11050
9412
96+
13650
9410
12255
11102
13671
10202
14500
10610
14450
13000
14050
11450
108+
17220
11882
15860
13700
17050
12770
18100
13780
17682
15470
17410
14500
120+
22100
14763
18610
16820
20202
16276
22750
16130
21845
18500
22100
17162
132+
25620
18100
22450
21320
24650
18770
26500
19322
27300
22100
25210
20740
–Т–Є–њ–∞–і–Ї–Є
x
=
2
{\displaystyle x=2}
x
=
3
{\displaystyle x=3}
A001157 A001158 A001159 A001160 A013954 A013955
–Ф–ї—П —Ж—Ц–ї–Є—Е, —П–Ї—Ц –љ–µ —Ф –Ї–≤–∞–і—А–∞—В–∞–Љ–Є, –Ї–Њ–ґ–µ–љ –і—Ц–ї—М–љ–Є–Ї d —З–Є—Б–ї–∞ n –Љ–∞—Ф –њ–Њ–≤'—П–Ј–∞–љ–Є–є –і—Ц–ї—М–љ–Є–Ї n/d, —Ц —В–Њ–Љ—Г –і–ї—П —В–∞–Ї–Є—Е —З–Є—Б–µ–ї
σ ѕГ -->
0
(
n
)
{\displaystyle \sigma _{0}(n)}
n
{\displaystyle {\sqrt {n}}}
σ ѕГ -->
0
(
n
)
{\displaystyle \sigma _{0}(n)}
σ ѕГ -->
0
(
p
)
=
2
σ ѕГ -->
0
(
p
n
)
=
n
+
1
σ ѕГ -->
1
(
p
)
=
p
+
1
{\displaystyle {\begin{aligned}\sigma _{0}(p)&=2\\\sigma _{0}(p^{n})&=n+1\\\sigma _{1}(p)&=p+1\end{aligned}}}
–Њ—Б–Ї—Ц–ї—М–Ї–Є, –Ј–∞ –Њ–Ј–љ–∞—З–µ–љ–љ—П–Љ, –њ—А–Њ—Б—В–µ —З–Є—Б–ї–Њ –і—Ц–ї–Є—В—М—Б—П —В—Ц–ї—М–Ї–Є –љ–∞ –Њ–і–Є–љ–Є—Ж—О —Ц —Б–∞–Љ–Њ–≥–Њ —Б–µ–±–µ.
σ ѕГ -->
0
(
p
n
# # -->
)
=
2
n
{\displaystyle \sigma _{0}(p_{n}\#)=2^{n}}
–Ф–ї—П –≤—Б—Ц—Е
n
>
2
{\displaystyle n>2}
1
<
σ ѕГ -->
0
(
n
)
<
n
{\displaystyle 1<\sigma _{0}(n)<n}
n
n
>
σ ѕГ -->
(
n
)
>
n
{\displaystyle n{\sqrt {n}}>\sigma (n)>n}
–Ф–ї—П —Б–Ї–ї–∞–і–µ–љ–Є—Е —З–Є—Б–µ–ї –≤–Є–Ї–Њ–љ—Г—Ф—В—М—Б—П –љ–µ—А—Ц–≤–љ—Ц—Б—В—М
σ ѕГ -->
(
n
)
>
n
+
n
1
2
{\displaystyle \sigma (n)>n+n^{\frac {1}{2}}}
[ 6]
–Ф–ї—П –±—Г–і—М-—П–Ї–Є—Е —Ж—Ц–ї–Є—Е —З–Є—Б–µ–ї –±—Ц–ї—М—И–Є—Е –Њ–і–Є–љ–Є—Ж—Ц
σ ѕГ -->
(
m
n
)
>
σ ѕГ -->
(
n
)
+
σ ѕГ -->
(
m
)
{\displaystyle \sigma (mn)>\sigma (n)+\sigma (m)\,}
–Ф–ї—П –≤—Б—Ц—Е
n
{\displaystyle n}
, [ 7] , [ 8]
σ ѕГ -->
(
n
)
<
6
π ѕА -->
2
⋅ вЛЕ -->
n
3
2
{\displaystyle \sigma (n)<{\frac {6}{\pi ^{2}}}\cdot n^{\frac {3}{2}}}
–Ф–ї—П –≤—Б—Ц—Е –љ–∞—В—Г—А–∞–ї—М–љ–Є—Е —З–Є—Б–µ–ї
n
{\displaystyle n}
m
{\displaystyle m}
σ ѕГ -->
m
(
n
)
≥ вЙ• -->
n
m
2
⋅ вЛЕ -->
σ ѕГ -->
0
(
n
)
{\displaystyle \sigma _{m}(n)\geq n^{\frac {m}{2}}\cdot \sigma _{0}(n)}
–Э–µ—А—Ц–≤–љ—Ц—Б—В—М –Ы–µ–љ–≥—Д–Њ—А–і–∞
σ ѕГ -->
(
n
)
≤ вЙ§ -->
1
2
(
n
+
1
)
σ ѕГ -->
0
(
n
)
{\displaystyle \sigma (n)\leq {\frac {1}{2}}(n+1)\sigma _{0}(n)}
–£ –Ї—Ц–ї—М—Ж—Ц –∞—А–Є—Д–Љ–µ—В–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є —Д—Г–љ–Ї—Ж—Ц—П –і—Ц–ї—М–љ–Є–Ї—Ц–≤ —Ф –Њ–±–Њ—А–Њ—В–љ–Є–Љ –µ–ї–µ–Љ–µ–љ—В–Њ–Љ —Ц –Љ–Њ–ґ–љ–∞ –і–∞—В–Є –µ–Ї–≤—Ц–≤–∞–ї–µ–љ—В–љ–µ –Њ–Ј–љ–∞—З–µ–љ–љ—П[ 9]
σ ѕГ -->
x
=
ι ќє -->
0
∗ вИЧ -->
ι ќє -->
x
,
{\displaystyle \sigma _{x}=\iota _{0}*\iota _{x},\,}
ι ќє -->
x
(
n
)
=
n
x
{\displaystyle \iota _{x}(n)=n^{x}}
–Ј–≥–Њ—А—В–Ї—Г –Ф—Ц—А—Ц—Е–ї–µ . –Ю–±–µ—А–љ–µ–љ–Є–Љ –µ–ї–µ–Љ–µ–љ—В–Њ–Љ –і–ї—П —Д—Г–љ–Ї—Ж—Ц—Ч ѕГx —Ф –Љ—Г–ї—М—В–Є–њ–ї—Ц–Ї–∞—В–Є–≤–љ–∞ –∞—А–Є—Д–Љ–µ—В–Є—З–љ–∞ —Д—Г–љ–Ї—Ж—Ц—П –Ј–∞–і–∞–љ–∞ —П–Ї[ 10]
(
σ ѕГ -->
x
− вИТ -->
1
)
(
p
k
)
=
{
1
,
k
=
0
− вИТ -->
1
− вИТ -->
p
x
,
k
=
1
p
x
,
k
=
2
0
,
k
>
2
{\displaystyle \left(\sigma _{x}^{-1}\right)(p^{k})={\begin{cases}1{\text{,}}&k=0\\-1-p^{x}{\text{,}}&k=1\\p^{x}{\text{,}}&k=2\\0{\text{,}}&k>2\end{cases}}}
σ ѕГ -->
x
− вИТ -->
1
=
(
ι ќє -->
x
μ ќЉ -->
)
∗ вИЧ -->
μ ќЉ -->
{\displaystyle \sigma _{x}^{-1}=(\iota _{x}\mu )*\mu \,}
x
=
0
{\displaystyle x=0}
σ ѕГ -->
0
− вИТ -->
1
=
μ ќЉ -->
∗ вИЧ -->
μ ќЉ -->
{\displaystyle \sigma _{0}^{-1}=\mu *\mu \,}
μ ќЉ -->
{\displaystyle \mu }
—Д—Г–љ–Ї—Ж—Ц—П –Ь–µ–±—Ц—Г—Б–∞ .
–Я—А–Є —В–Є—Е –ґ–µ –њ–Њ–Ј–љ–∞—З–µ–љ–љ—П—Е
σ ѕГ -->
− вИТ -->
x
=
ι ќє -->
− вИТ -->
x
σ ѕГ -->
x
.
{\displaystyle \sigma _{-x}=\iota _{-x}\sigma _{x}.\,}
–ѓ–Ї—Й–Њ
m
,
n
{\displaystyle m,n}
–≤–Ј–∞—Ф–Љ–љ–Њ –њ—А–Њ—Б—В—Ц –љ–∞—В—Г—А–∞–ї—М–љ—Ц —З–Є—Б–ї–∞, —Ц
d
∗ вИЧ -->
|
m
n
{\displaystyle d^{*}|mn}
d
∗ вИЧ -->
=
d
d
′
{\displaystyle d^{*}=dd'}
d
|
m
{\displaystyle d|m}
d
′
|
m
{\displaystyle d'|m}
d
|
m
{\displaystyle d|m}
d
′
|
n
{\displaystyle d'|n}
d
d
′
|
m
n
{\displaystyle dd'|mn}
∑ вИС -->
d
|
m
d
x
∑ вИС -->
d
′
|
n
(
d
′
)
x
=
∑ вИС -->
d
∗ вИЧ -->
|
m
n
(
d
∗ вИЧ -->
)
x
{\displaystyle \sum _{d|m}d^{x}\sum _{d'|n}(d')^{x}=\sum _{d^{*}|mn}(d^{*})^{x}}
σ ѕГ -->
x
(
m
)
σ ѕГ -->
x
(
n
)
=
σ ѕГ -->
x
(
m
n
)
{\displaystyle \sigma _{x}(m)\sigma _{x}(n)=\sigma _{x}(mn)}
–Э–∞—В–Њ–Љ—Ц—Б—В—М, –љ–∞–њ—А–Є–Ї–ї–∞–і,
σ ѕГ -->
x
(
2
)
=
1
+
2
x
,
σ ѕГ -->
x
(
4
)
=
1
+
2
x
+
4
x
{\displaystyle \sigma _{x}(2)=1+2^{x},\ \sigma _{x}(4)=1+2^{x}+4^{x}}
σ ѕГ -->
x
(
2
)
⋅ вЛЕ -->
σ ѕГ -->
x
(
2
)
=
1
+
2
⋅ вЛЕ -->
2
x
+
4
x
≠ вЙ† -->
σ ѕГ -->
x
(
4
)
=
1
+
2
x
+
4
x
{\displaystyle \sigma _{x}(2)\cdot \sigma _{x}(2)=1+2\cdot 2^{x}+4^{x}\neq \sigma _{x}(4)=1+2^{x}+4^{x}}
–ѓ–Ї—Й–Њ –Ј–∞–њ–Є—Б–∞—В–Є
n
=
∏ вИП -->
i
=
1
r
p
i
a
i
{\displaystyle n=\prod _{i=1}^{r}p_{i}^{a_{i}}}
–і–µ r = ѕЙ (n ) вАФ –Ї—Ц–ї—М–Ї—Ц—Б—В—М –њ—А–Њ—Б—В–Є—Е –і—Ц–ї—М–љ–Є–Ї—Ц–≤ —З–Є—Б–ї–∞ n , pi вАФ i -–є –њ—А–Њ—Б—В–Є–є –і—Ц–ї—М–љ–Є–Ї, –∞ ai вАФ –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Є–є —Б—В–µ–њ—Ц–љ—М pi , –љ–∞ —П–Ї–Є–є –і—Ц–ї–Є—В—М—Б—П n , —В–Њ –Ј –Љ—Г–ї—М—В–Є–њ–ї—Ц–Ї–∞—В–Є–≤–љ–Њ—Б—В—Ц —Д—Г–љ–Ї—Ж—Ц—Ч –і—Ц–ї—М–љ–Є–Ї—Ц–≤ –Њ—В—А–Є–Љ—Г—Ф–Љ–Њ:
σ ѕГ -->
x
(
n
)
=
∏ вИП -->
i
=
1
r
∑ вИС -->
j
=
0
a
i
p
i
j
x
=
∏ вИП -->
i
=
1
r
(
1
+
p
i
x
+
p
i
2
x
+
⋯ вЛѓ -->
+
p
i
a
i
x
)
.
{\displaystyle \sigma _{x}(n)=\prod _{i=1}^{r}\sum _{j=0}^{a_{i}}p_{i}^{jx}=\prod _{i=1}^{r}(1+p_{i}^{x}+p_{i}^{2x}+\cdots +p_{i}^{a_{i}x}).}
–Т–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—З–Є —Д–Њ—А–Љ—Г–ї—Г —Б—Г–Љ–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Њ—Ч –њ—А–Њ–≥—А–µ—Б—Ц—Ч , —В–∞–Ї–Њ–ґ –Љ–Њ–ґ–љ–∞ –Ј–∞–њ–Є—Б–∞–Љ–Є:
σ ѕГ -->
x
(
n
)
=
∏ вИП -->
i
=
1
r
p
i
(
a
i
+
1
)
x
− вИТ -->
1
p
i
x
− вИТ -->
1
{\displaystyle \sigma _{x}(n)=\prod _{i=1}^{r}{\frac {p_{i}^{(a_{i}+1)x}-1}{p_{i}^{x}-1}}}
–ѓ–Ї—Й–Њ —Г –њ–Њ–њ–µ—А–µ–і–љ—Ц–є —Д–Њ—А–Љ—Г–ї—Ц –≤–Ј—П—В–Є x = 0, –Њ—В—А–Є–Љ–∞—Ф–Љ–Њ, —Й–Њ d (n ) —Ф —А—Ц–≤–љ–Є–Љ:
σ ѕГ -->
0
(
n
)
=
∏ вИП -->
i
=
1
r
(
a
i
+
1
)
.
{\displaystyle \sigma _{0}(n)=\prod _{i=1}^{r}(a_{i}+1).}
–Я—А–Є–Ї–ї–∞–і n = 24 –Љ–∞—Ф –і–≤–∞ –њ—А–Њ—Б—В–Є—Е –і—Ц–ї—М–љ–Є–Ї–Є вАФ p1 = 2 —Ц p2 = 3. –Ю—Б–Ї—Ц–ї—М–Ї–Є 24 вАФ –і–Њ–±—Г—В–Њ–Ї 23 √Ч31 , —В–Њ a 1 = 3 —Ц a 2 = 1.–Ґ–µ–њ–µ—А –Љ–Њ–ґ–љ–∞ –Њ–±—З–Є—Б–ї–Є—В–Є
σ ѕГ -->
0
(
24
)
{\displaystyle \sigma _{0}(24)}
σ ѕГ -->
0
(
24
)
=
∏ вИП -->
i
=
1
2
(
a
i
+
1
)
=
(
3
+
1
)
(
1
+
1
)
=
4
× √Ч -->
2
=
8.
{\displaystyle {\begin{aligned}\sigma _{0}(24)&=\prod _{i=1}^{2}(a_{i}+1)\\&=(3+1)(1+1)=4\times 2=8.\end{aligned}}}
–Т—Ц—Б—Ц–Љ –і—Ц–ї—М–љ–Є–Ї—Ц–≤ —З–Є—Б–ї–∞ 24 вАФ 1, 2, 4, 8, 3, 6, 12 —Ц 24. –ѓ–Ї—Й–Њ n вАФ —Б—В–µ–њ—Ц–љ—М –і–≤—Ц–є–Ї–Є, —В–Њ–±—В–Њ
n
=
2
k
{\displaystyle n=2^{k}}
σ ѕГ -->
(
n
)
=
2
× √Ч -->
2
k
− вИТ -->
1
=
2
n
− вИТ -->
1
,
{\displaystyle \sigma (n)=2\times 2^{k}-1=2n-1,}
s (n ) = n -1, —Й–Њ —А–Њ–±–Є—В—М n –Љ–∞–є–ґ–µ –і–Њ—Б–Ї–Њ–љ–∞–ї–Є–Љ . –ѓ–Ї –њ—А–Є–Ї–ї–∞–і, –і–ї—П –і–≤–Њ—Е –њ—А–Њ—Б—В–Є—Е p —Ц q (–і–µ p < q ), –љ–µ—Е–∞–є
n
=
p
q
.
{\displaystyle n=pq.}
–Ґ–Њ–і—Ц
σ ѕГ -->
(
n
)
=
(
p
+
1
)
(
q
+
1
)
=
n
+
1
+
(
p
+
q
)
,
{\displaystyle \sigma (n)=(p+1)(q+1)=n+1+(p+q),}
ϕ ѕХ -->
(
n
)
=
(
p
− вИТ -->
1
)
(
q
− вИТ -->
1
)
=
n
+
1
− вИТ -->
(
p
+
q
)
,
{\displaystyle \phi (n)=(p-1)(q-1)=n+1-(p+q),}
—Ц
n
+
1
=
(
σ ѕГ -->
(
n
)
+
ϕ ѕХ -->
(
n
)
)
/
2
,
{\displaystyle n+1=(\sigma (n)+\phi (n))/2,}
p
+
q
=
(
σ ѕГ -->
(
n
)
− вИТ -->
ϕ ѕХ -->
(
n
)
)
/
2
,
{\displaystyle p+q=(\sigma (n)-\phi (n))/2,}
–і–µ ѕЖ (n ) вАФ —Д—Г–љ–Ї—Ж—Ц—П –Х–є–ї–µ—А–∞ . –Ґ–Њ–і—Ц –Ї–Њ—А–µ–љ—Ц p —Ц q —А—Ц–≤–љ—П–љ–љ—П:
(
x
− вИТ -->
p
)
(
x
− вИТ -->
q
)
=
x
2
− вИТ -->
(
p
+
q
)
x
+
n
=
x
2
− вИТ -->
[
(
σ ѕГ -->
(
n
)
− вИТ -->
ϕ ѕХ -->
(
n
)
)
/
2
]
x
+
[
(
σ ѕГ -->
(
n
)
+
ϕ ѕХ -->
(
n
)
)
/
2
− вИТ -->
1
]
=
0
{\displaystyle (x-p)(x-q)=x^{2}-(p+q)x+n=x^{2}-[(\sigma (n)-\phi (n))/2]x+[(\sigma (n)+\phi (n))/2-1]=0}
–Љ–Њ–ґ–љ–∞ –≤–Є—А–∞–Ј–Є—В–Є —З–µ—А–µ–Ј ѕГ (n ) –Є ѕЖ (n ) :
p
=
(
σ ѕГ -->
(
n
)
− вИТ -->
ϕ ѕХ -->
(
n
)
)
/
4
− вИТ -->
[
(
σ ѕГ -->
(
n
)
− вИТ -->
ϕ ѕХ -->
(
n
)
)
/
4
]
2
− вИТ -->
[
(
σ ѕГ -->
(
n
)
+
ϕ ѕХ -->
(
n
)
)
/
2
− вИТ -->
1
]
,
{\displaystyle p=(\sigma (n)-\phi (n))/4-{\sqrt {[(\sigma (n)-\phi (n))/4]^{2}-[(\sigma (n)+\phi (n))/2-1]}},}
q
=
(
σ ѕГ -->
(
n
)
− вИТ -->
ϕ ѕХ -->
(
n
)
)
/
4
+
[
(
σ ѕГ -->
(
n
)
− вИТ -->
ϕ ѕХ -->
(
n
)
)
/
4
]
2
− вИТ -->
[
(
σ ѕГ -->
(
n
)
+
ϕ ѕХ -->
(
n
)
)
/
2
− вИТ -->
1
]
.
{\displaystyle q=(\sigma (n)-\phi (n))/4+{\sqrt {[(\sigma (n)-\phi (n))/4]^{2}-[(\sigma (n)+\phi (n))/2-1]}}.}
–Ч–љ–∞—О—З–Є n —Ц –∞–±–Њ ѕГ (n ), –∞–±–Њ ѕЖ (n ) (—З–Є –Ј–љ–∞—О—З–Є p+q —Ц –∞–±–Њ ѕГ (n ) –∞–±–Њ ѕЖ (n )) –Љ–Њ–ґ–љ–∞ –Ј–љ–∞–є—В–Є p —Ц q . –Т 1984 —А–Њ—Ж—Ц –•—Ц–Ј-–С—А–∞—Г–љ (Roger Heath-Brown) –і–Њ–≤—Ц–≤, —Й–Њ —А—Ц–≤–љ—Ц—Б—В—М
σ ѕГ -->
0
(
n
)
=
σ ѕГ -->
0
(
n
+
1
)
{\displaystyle \sigma _{0}(n)=\sigma _{0}(n+1)}
–≤–Є–Ї–Њ–љ—Г—Ф—В—М—Б—П –і–ї—П –љ–µ—Б–Ї—Ц–љ—З–µ–љ–љ–Њ—Ч –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц –љ–∞—В—Г—А–∞–ї—М–љ–Є—Е —З–Є—Б–µ–ї.
–Ф–≤–∞ —А—П–і–Є –Ф—Ц—А—Ц—Е–ї–µ , —Ц–Ј —Д—Г–љ–Ї—Ж—Ц—Ф—О –і—Ц–ї—М–љ–Є–Ї—Ц–≤:
∑ вИС -->
n
=
1
∞ вИЮ -->
σ ѕГ -->
a
(
n
)
n
s
=
ζ ќґ -->
(
s
)
ζ ќґ -->
(
s
− вИТ -->
a
)
,
{\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)}{n^{s}}}=\zeta (s)\zeta (s-a),}
—Ц –њ—А–Є –њ–Њ–Ј–љ–∞—З–µ–љ–љ—Ц d (n ) = ѕГ 0 (n ) –Ј–Њ–Ї—А–µ–Љ–∞
∑ вИС -->
n
=
1
∞ вИЮ -->
d
(
n
)
n
s
=
ζ ќґ -->
2
(
s
)
,
{\displaystyle \sum _{n=1}^{\infty }{\frac {d(n)}{n^{s}}}=\zeta ^{2}(s),}
–Ж–љ—И–Є–є —А—П–і, –і–µ –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—В—М—Б—П —Ж—Ц —Д—Г–љ–Ї—Ж—Ц—Ч:
∑ вИС -->
n
=
1
∞ вИЮ -->
σ ѕГ -->
a
(
n
)
σ ѕГ -->
b
(
n
)
n
s
=
ζ ќґ -->
(
s
)
ζ ќґ -->
(
s
− вИТ -->
a
)
ζ ќґ -->
(
s
− вИТ -->
b
)
ζ ќґ -->
(
s
− вИТ -->
a
− вИТ -->
b
)
ζ ќґ -->
(
2
s
− вИТ -->
a
− вИТ -->
b
)
.
{\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)\sigma _{b}(n)}{n^{s}}}={\frac {\zeta (s)\zeta (s-a)\zeta (s-b)\zeta (s-a-b)}{\zeta (2s-a-b)}}.}
–†—П–і –Ы–∞–Љ–±–µ—А–∞ , —Ц–Ј —Д—Г–љ–Ї—Ж—Ц—Ф—О –і—Ц–ї—М–љ–Є–Ї—Ц–≤:
∑ вИС -->
n
=
1
∞ вИЮ -->
q
n
σ ѕГ -->
a
(
n
)
=
∑ вИС -->
n
=
1
∞ вИЮ -->
n
a
q
n
1
− вИТ -->
q
n
{\displaystyle \sum _{n=1}^{\infty }q^{n}\sigma _{a}(n)=\sum _{n=1}^{\infty }{\frac {n^{a}q^{n}}{1-q^{n}}}}
–і–ї—П –±—Г–і—М-—П–Ї–Њ–≥–Њ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ–≥–Њ |q | вЙ§ 1 —Ц a .
–¶—П —Б—Г–Љ–∞ –Ј—Г—Б—В—А—Ц—З–∞—Ф—В—М—Б—П —В–∞–Ї–Њ–ґ –≤ —А—П–і–∞—Е –§—Г—А'—Ф –і–ї—П —А—П–і—Ц–≤ –Х–є–Ј–µ–љ—И—В–µ–є–љ–∞ —Ц –≤ —Ц–љ–≤–∞—А—Ц–∞–љ—В–∞—Е –µ–ї—Ц–њ—В–Є—З–љ–Є—Е —Д—Г–љ–Ї—Ж—Ц–є –Т–µ–є—Ф—А—И—В—А–∞—Б–∞ .
–Ф–ї—П –≤—Б—Ц—Е
ε ќµ -->
>
0
{\displaystyle \varepsilon >0}
–≥—А–∞–љ–Є—Ж—П :
lim
¯ ¬ѓ -->
n
→ вЖТ -->
∞ вИЮ -->
вБ° -->
d
(
n
)
(
log
вБ° -->
n
)
ε ќµ -->
=
∞ вИЮ -->
.
{\displaystyle \varlimsup _{n\to \infty }{\frac {d(n)}{(\log n)^{\varepsilon }}}=\infty .}
–Ф—Ц–є—Б–љ–Њ –Љ–Њ–ґ–љ–∞ –≤–Є–±—А–∞—В–Є —В–∞–Ї–µ —Ж—Ц–ї–µ —З–Є—Б–ї–Њ
k
{\displaystyle k}
k
⩽ в©љ -->
ε ќµ -->
<
k
+
1
{\displaystyle k\leqslant \varepsilon <k+1}
p
k
{\displaystyle p_{k}}
k -—В–µ –њ–Њ –≤–µ–ї–Є—З–Є–љ—Ц –њ—А–Њ—Б—В–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–љ–∞ –≤–≤–µ—Б—В–Є —З–Є—Б–ї–∞
n
i
=
(
2
⋅ вЛЕ -->
3
⋅ вЛЕ -->
… вА¶ -->
⋅ вЛЕ -->
p
k
)
i
{\displaystyle n_{i}=(2\cdot 3\cdot \ldots \cdot p_{k})^{i}}
i
∈ вИИ -->
N
{\displaystyle i\in \mathbb {N} }
d
(
n
i
)
=
(
i
+
1
)
k
+
1
>
i
k
+
1
=
(
log
вБ° -->
n
i
log
вБ° -->
(
2
⋅ вЛЕ -->
… вА¶ -->
⋅ вЛЕ -->
p
k
+
1
)
)
k
+
1
>
c
(
log
вБ° -->
n
i
)
k
+
1
{\displaystyle d(n_{i})=(i+1)^{k+1}>i^{k+1}=\left({\frac {\log n_{i}}{\log(2\cdot \ldots \cdot p_{k+1})}}\right)^{k+1}>c(\log n_{i})^{k+1}}
c
{\displaystyle c}
i
{\displaystyle i}
δ ќі -->
=
k
+
1
− вИТ -->
ε ќµ -->
{\displaystyle \delta =k+1-\varepsilon }
lim
i
→ вЖТ -->
∞ вИЮ -->
d
(
n
i
)
(
log
вБ° -->
n
i
)
ε ќµ -->
>
lim
i
→ вЖТ -->
∞ вИЮ -->
c
(
log
вБ° -->
n
i
)
δ ќі -->
=
∞ вИЮ -->
.
{\displaystyle \lim _{i\to \infty }{\frac {d(n_{i})}{(\log n_{i})^{\varepsilon }}}>\lim _{i\to \infty }c(\log n_{i})^{\delta }=\infty .}
–Ч —Ц–љ—И–Њ–≥–Њ –±–Њ–Ї—Г —Д—Г–љ–Ї—Ж—Ц—П –Ї—Ц–ї—М–Ї–Њ—Б—В—Ц –і—Ц–ї—М–љ–Є–Ї—Ц–≤ –Ј–∞–і–Њ–≤–Њ–ї—М–љ—П—Ф –љ–µ—А—Ц–≤–љ—Ц—Б—В—М[ 11] –і–ї—П –≤—Б—Ц—Е
ϵ ѕµ -->
>
0
,
d
(
n
)
=
o
(
n
ϵ ѕµ -->
)
{\displaystyle \epsilon >0,\quad d(n)=o(n^{\epsilon })}
lim
n
→ вЖТ -->
∞ вИЮ -->
d
(
n
)
n
ε ќµ -->
=
0.
{\displaystyle \lim _{n\to \infty }{\frac {d(n)}{n^{\varepsilon }}}=0.}
–°–µ–≤–µ—А–Є–љ –Т—Ц–≥–µ—А—В –і–∞–≤ –±—Ц–ї—М—И —В–Њ—З–љ—Г –Њ—Ж—Ц–љ–Ї—Г
lim
¯ ¬ѓ -->
n
→ вЖТ -->
∞ вИЮ -->
вБ° -->
log
вБ° -->
d
(
n
)
log
вБ° -->
n
/
log
вБ° -->
log
вБ° -->
n
=
log
вБ° -->
2.
{\displaystyle \varlimsup _{n\to \infty }{\frac {\log d(n)}{\log n/\log \log n}}=\log 2.}
lim
_ _ -->
n
→ вЖТ -->
∞ вИЮ -->
вБ° -->
d
(
n
)
=
2.
{\displaystyle \varliminf _{n\to \infty }d(n)=2.}
–Ф—Ц—А—Ц—Е–ї–µ –њ–Њ–Ї–∞–Ј–∞–≤, —Й–Њ —Б–µ—А–µ–і–љ—Ц–є –њ–Њ—А—П–і–Њ–Ї —Д—Г–љ–Ї—Ж—Ц—Ч –і—Ц–ї—М–љ–Є–Ї—Ц–≤ –Ј–∞–і–Њ–≤–Њ–ї—М–љ—П—Ф –љ–µ—А—Ц–≤–љ—Ц—Б—В—М:–Ф–ї—П –≤—Б—Ц—Е
x
≥ вЙ• -->
1
,
∑ вИС -->
n
≤ вЙ§ -->
x
d
(
n
)
=
x
log
вБ° -->
x
+
(
2
γ ќ≥ -->
− вИТ -->
1
)
x
+
O
(
x
)
,
{\displaystyle x\geq 1,\sum _{n\leq x}d(n)=x\log x+(2\gamma -1)x+O({\sqrt {x}}),}
–і–µ
γ ќ≥ -->
{\displaystyle \gamma }
—Б—В–∞–ї–∞ –Х–є–ї–µ—А–∞ вАФ –Ь–∞—Б–Ї–µ—А–Њ–љ—Ц .
–Ч–∞–≤–і–∞–љ–љ—П –њ–Њ–Ї—А–∞—Й–Є—В–Є –≥—А–∞–љ–Є—Ж—О
O
(
x
)
{\displaystyle O({\sqrt {x}})}
–Я–Њ–≤–µ–і—Ц–љ–Ї–∞ —Б–Є–≥–Љ–∞ —Д—Г–љ–Ї—Ж—Ц—Ч —Ф –љ–µ—А—Ц–≤–љ–Њ–Љ—Ц—А–љ–Њ—О. –Р—Б–Є–Љ–њ—В–Њ—В–Є—З–љ—Г —И–≤–Є–і–Ї—Ц—Б—В—М —А–Њ—Б—В—Г —Б–Є–≥–Љ–∞ —Д—Г–љ–Ї—Ж—Ц—Ч –Љ–Њ–ґ–љ–∞ –≤–Є—А–∞–Ј–Є—В–Є —Д–Њ—А–Љ—Г–ї–Њ—О:
lim
¯ ¬ѓ -->
n
→ вЖТ -->
∞ вИЮ -->
вБ° -->
σ ѕГ -->
(
n
)
n
log
вБ° -->
log
вБ° -->
n
=
e
γ ќ≥ -->
.
{\displaystyle \varlimsup _{n\rightarrow \infty }{\frac {\sigma (n)}{n\,\log \log n}}=e^{\gamma }.}
–¶–µ–є —А–µ–Ј—Г–ї—М—В–∞—В –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —В–µ–Њ—А–µ–Љ–Њ—О –У—А–Њ–љ–≤–∞–ї–∞ (Gronwall) —Ц –±—Г–≤ –Њ–њ—Г–±–ї—Ц–Ї–Њ–≤–∞–љ–Є–є —Г 1913 —А–Њ—Ж—Ц [ 12] —В—А–µ—В—О —В–µ–Њ—А–µ–Љ—Г –Ь–µ—А—В–µ–љ—Б–∞ , —П–Ї–∞ —Б—В–≤–µ—А–і–ґ—Г—Ф, —Й–Њ
lim
n
→ вЖТ -->
∞ вИЮ -->
1
log
вБ° -->
n
∏ вИП -->
p
≤ вЙ§ -->
n
p
p
− вИТ -->
1
=
e
γ ќ≥ -->
,
{\displaystyle \lim _{n\to \infty }{\frac {1}{\log n}}\prod _{p\leq n}{\frac {p}{p-1}}=e^{\gamma },}
–і–µ p вАФ –њ—А–Њ—Б—В–µ —З–Є—Б–ї–Њ .
σ ѕГ -->
(
n
)
<
e
γ ќ≥ -->
n
log
вБ° -->
log
вБ° -->
n
{\displaystyle \ \sigma (n)<e^{\gamma }n\log \log n}
–≤–Є–Ї–Њ–љ—Г—Ф—В—М—Б—П –і–ї—П –≤—Б—Ц—Е –і–Њ—Б–Є—В—М –≤–µ–ї–Є–Ї–Є—Е n [ 13]
–£ 1984 —А–Њ—Ж—Ц –У–∞–є –†–Њ–±—Ц–љ –і–Њ–≤—Ц–≤, —Й–Њ –љ–µ—А—Ц–≤–љ—Ц—Б—В—М —Ф –≤—Ц—А–љ–Њ—О –і–ї—П –≤—Б—Ц—Е n вЙ• 5041 –≤ —В–Њ–Љ—Г —Ц —В—Ц–ї—М–Ї–Є –≤ —В–Њ–Љ—Г –≤–Є–њ–∞–і–Ї—Г, —П–Ї—Й–Њ –≥—Ц–њ–Њ—В–µ–Ј–∞ –†—Ц–Љ–∞–љ–∞ —Ф –≤—Ц—А–љ–Њ—О [ 14] —В–µ–Њ—А–µ–Љ–Њ—О –†–Њ–±—Ц–љ–∞ .
–Э–∞–є–±—Ц–ї—М—И–µ –≤—Ц–і–Њ–Љ–µ —З–Є—Б–ї–Њ, —Й–Њ –њ–Њ—А—Г—И—Г—Ф –љ–µ—А—Ц–≤–љ—Ц—Б—В—М –†–Њ–±—Ц–љ–∞ вАФ n = 5040. –ѓ–Ї—Й–Њ –≥—Ц–њ–Њ—В–µ–Ј–∞ –†—Ц–Љ–∞–љ–∞ –≤—Ц—А–љ–∞, —В–Њ –љ–µ–Љ–∞—Ф –±—Ц–ї—М—И–Є—Е —З–Є—Б–µ–ї, —Й–Њ –њ–Њ—А—Г—И—Г—О—В—М –љ–µ—А—Ц–≤–љ—Ц—Б—В—М. –†–Њ–±—Ц–љ –њ–Њ–Ї–∞–Ј–∞–≤, —Й–Њ –≤ —А–∞–Ј—Ц –њ–Њ–Љ–Є–ї–Ї–Њ–≤–Њ—Б—В—Ц –≥—Ц–њ–Њ—В–µ–Ј–Є —Ц—Б–љ—Г—Ф –љ–µ—Б–Ї—Ц–љ—З–µ–љ–љ–∞ –Ї—Ц–ї—М–Ї—Ц—Б—В—М —З–Є—Б–µ–ї n , —Й–Њ –њ–Њ—А—Г—И—Г—О—В—М –љ–µ—А—Ц–≤–љ—Ц—Б—В—М, —Ц –≤—Ц–і–Њ–Љ–Њ, —Й–Њ –љ–∞–є–Љ–µ–љ—И–µ –Ј —В–∞–Ї–Є—Е —З–Є—Б–µ–ї n вЙ• 5041 –Љ–∞—Ф –±—Г—В–Є –љ–∞–і–ї–Є—И–Ї–Њ–≤–Є–Љ —З–Є—Б–ї–Њ–Љ [ 15] –≤—Ц–ї—М–љ–Є—Е –≤—Ц–і –Ї–≤–∞–і—А–∞—В—Ц–≤ —З–Є—Б–µ–ї , —Ц —Й–Њ –≥—Ц–њ–Њ—В–µ–Ј–∞ –†—Ц–Љ–∞–љ–∞ –µ–Ї–≤—Ц–≤–∞–ї–µ–љ—В–љ–∞ –≤–Є–Ї–Њ–љ–∞–љ–љ—О –љ–µ—А—Ц–≤–љ–Њ—Б—В—Ц –і–ї—П –≤—Б—Ц—Е —З–Є—Б–µ–ї n , —Й–Њ –і—Ц–ї—П—В—М—Б—П –љ–∞ –њ'—П—В–Є–є —Б—В–µ–њ—Ц–љ—М –њ—А–Њ—Б—В–Њ–≥–Њ —З–Є—Б–ї–∞ [ 16] –Ф–ґ–µ—Д—А—Ц –Ы–∞–≥–∞—А—Ц–∞—Б (Jeffrey Lagarias) –≤ 2002 —А–Њ—Ж—Ц –і–Њ–≤—Ц–≤, —Й–Њ –≥—Ц–њ–Њ—В–µ–Ј–∞ –†—Ц–Љ–∞–љ–∞ –µ–Ї–≤—Ц–≤–∞–ї–µ–љ—В–љ–∞ —В–≤–µ—А–і–ґ–µ–љ–љ—П–Љ
σ ѕГ -->
(
n
)
≤ вЙ§ -->
H
n
+
ln
вБ° -->
(
H
n
)
e
H
n
{\displaystyle \sigma (n)\leq H_{n}+\ln(H_{n})e^{H_{n}}}
–і–ї—П –±—Г–і—М-—П–Ї–Њ–≥–Њ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–≥–Њ n , –і–µ
H
n
{\displaystyle H_{n}}
n -–µ –≥–∞—А–Љ–Њ–љ—Ц—З–љ–µ —З–Є—Б–ї–Њ [ 17] –†–Њ–±—Ц–љ –і–Њ–≤—Ц–≤, —Й–Њ –љ–µ—А—Ц–≤–љ—Ц—Б—В—М
σ ѕГ -->
(
n
)
<
e
γ ќ≥ -->
n
log
вБ° -->
log
вБ° -->
n
+
0.6483
n
log
вБ° -->
log
вБ° -->
n
{\displaystyle \ \sigma (n)<e^{\gamma }n\log \log n+{\frac {0.6483\ n}{\log \log n}}}
–≤–Є–Ї–Њ–љ—Г—Ф—В—М—Б—П –і–ї—П n вЙ• 3 –±–µ–Ј –±—Г–і—М-—П–Ї–Є—Е –і–Њ–і–∞—В–Ї–Њ–≤–Є—Е —Г–Љ–Њ–≤.
вЖС Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: DC Heath and Company, LCCN 77-171950 —Б—В–Њ—А 46
вЖС –њ–Њ—Б–ї—Ц–і–Њ–≤–љ—Ц—Б—В—М A000005 –Ј –Ю–љ–ї–∞–є–љ –µ–љ—Ж–Є–Ї–ї–Њ–њ–µ–і—Ц—Ч –њ–Њ—Б–ї—Ц–і–Њ–≤–љ–Њ—Б—В–µ–є —Ж—Ц–ї–Є—Е —З–Є—Б–µ–ї , OEIS
вЖС Pettofrezzo, Anthony J .; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766
, –°—В–Њ—А 58
вЖС –њ–Њ—Б–ї—Ц–і–Њ–≤–љ—Ц—Б—В—М A000203 –Ј –Ю–љ–ї–∞–є–љ –µ–љ—Ж–Є–Ї–ї–Њ–њ–µ–і—Ц—Ч –њ–Њ—Б–ї—Ц–і–Њ–≤–љ–Њ—Б—В–µ–є —Ж—Ц–ї–Є—Е —З–Є—Б–µ–ї , OEIS
вЖС –њ–Њ—Б–ї—Ц–і–Њ–≤–љ—Ц—Б—В—М A001065 –Ј –Ю–љ–ї–∞–є–љ –µ–љ—Ж–Є–Ї–ї–Њ–њ–µ–і—Ц—Ч –њ–Њ—Б–ї—Ц–і–Њ–≤–љ–Њ—Б—В–µ–є —Ж—Ц–ї–Є—Е —З–Є—Б–µ–ї , OEIS
вЖС Mitrinovic D. S., Sandor J., Crstici B., Handbook of Number Theory , Kluwer Academic Publishers, 1996, ISBN 0-7923-3823-5 , III.
вЖС Annapurna V., Inequalities of ѕГ(n) and ѕЖ(n) , Math. Mag., 45 , 1972, —Б—В—А. 187 вАУ 190
вЖС Mitrinovic D. S., Sandor J., Crstici B., Handbook of Number Theory , Kluwer Academic Publishers, 1996, ISBN 0-7923-3823-5 , III.
вЖС Bundschuh, P., Einf√Љhrung in die Zahlentheorie , Springer-Verlag, 1991, ISBN 3-540-55178-6 , 1.4.10
вЖС Siemon, H., Einf√Љhrung in die Zahlentheorie , Verlag Dr. Kovac, Hamburg, 2002, ISSN 1435 вАУ 6511, 5.5, 8.15.4 –Є 8.7
вЖС "Apostol Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3 , MR 0434929, Zbl 0335.10001
вЖС Gronwall, Thomas Hakon (1913), ¬ЂSome asymptotic expressions in the theory of numbers¬ї, Transactions of the American Mathematical Society 14: 113 -122, doi: 10.1090 / S0002-9947-1913-1500940-6
вЖС Ramanujan, Srinivasa (1997), ¬ЂHighly composite numbers, annotated by Jean-Louis Nicolas and Guy Robin¬ї, The Ramanujan Journal 1 (2): 119-153, doi: 10.1023 / A: 1009764017495, ISSN 1382-4090, MR 1606180
вЖС Robin, Guy (1984), ¬ЂGrandes valeurs de la fonction somme des diviseurs et hypothese de Riemann¬ї, Journal de Mathematiques Pures et Appliquees, Neuvieme Serie 63 (2 ): 187-213, ISSN 0021-7824, MR 774171
вЖС Akbary, Amir; Friggstad, Zachary (2009), ¬ЂSuperabundant numbers and the Riemann hypothesis¬ї, American Mathematical Monthly 116 (3): 273-275, doi: 10.4169 / 193009709X470128
вЖС YoungJu Choie, Nicolas Lichiardopol, Pieter Moree, Patrick Sole On Robin's criterion for the Riemann hypothesis 2007 Journal de theorie des nombres de Bordeaux, ISSN = 1246-7405, v19, issue 2, pages = 357-372
вЖС Lagarias, Jeffrey C. (2002) , ¬ЂAn elementary problem equivalent to the Riemann hypothesis¬ї, The American Mathematical Monthly 109 (6): 534-543, doi: 10.2307 / 2695443, ISSN 0002-9890, JSTOR 2695443, MR 19080
–І–∞–љ–і—А–∞—Б–µ–Ї—Е–∞—А–∞–љ –Ъ. –Т–≤–µ–і–µ–љ–Є–µ –≤ –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї—Г—О —В–µ–Њ—А–Є—О —З–Є—Б–µ–ї . вАФ –Ь–Њ—Б–Ї–≤–∞ : –Ь–Є—А , 1974. вАФ 187 —Б.(—А–Њ—Б.) Apostol Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3 , MR 0434929, Zbl 0335.10001
Bach, Eric; Shallit, Jeffrey, Algorithmic Number Theory , volume 1, 1996, MIT Press. ISBN 0-262-02405-5 , see page 234 in section 8.8.
Weisstein, Eric W. Robin's Theorem (–∞–љ–≥–ї.) –љ–∞ —Б–∞–є—В—Ц Wolfram MathWorld .Elementary Evaluation of Certain Convolution Sums Involving Divisor Functions
–Ч–∞–≥–∞–ї—М–љ—Ц –≤—Ц–і–Њ–Љ–Њ—Б—В—Ц –§–∞–Ї—В–Њ—А–Є–Ј–∞—Ж—Ц–є–љ—Ц —Д–Њ—А–Љ–Є –Ч –Њ–±–Љ–µ–ґ–µ–љ–Є–Љ–Є –І–Є—Б–ї–∞ –Ј –±–∞–≥–∞—В—М–Љ–∞ –Я–Њ–≤'—П–Ј–∞–љ—Ц –Ј –∞–ї—Ц–Ї–≤–Њ—В–љ–Є–Љ–Є –Ж–љ—И–µ











































































![{\displaystyle (x-p)(x-q)=x^{2}-(p+q)x+n=x^{2}-[(\sigma (n)-\phi (n))/2]x+[(\sigma (n)+\phi (n))/2-1]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6ed7a9738564d7c4116838b5b780c4b05b4754f)
![{\displaystyle p=(\sigma (n)-\phi (n))/4-{\sqrt {[(\sigma (n)-\phi (n))/4]^{2}-[(\sigma (n)+\phi (n))/2-1]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaa8761980df82ffe7850ae219721a81a02ff0f2)
![{\displaystyle q=(\sigma (n)-\phi (n))/4+{\sqrt {[(\sigma (n)-\phi (n))/4]^{2}-[(\sigma (n)+\phi (n))/2-1]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42a4dc6f0dfa3cab8af78ec78de3fbdffd970b86)































