Основні поняття теорії програмних інваріантів
|
Read other articles:

American actor (born 1972) For other people named Christopher Barnes, see Christopher Barnes (disambiguation). Christopher Daniel BarnesBarnes in 2022Born (1972-11-07) November 7, 1972 (age 51)Portland, Maine, U.S.Other namesC. B. Barnes, C. D. Barnes, Chris BarnesOccupationsActorwriterchild modelYears active1981–presentWebsitechristopherdanielbarnes.com Christopher Daniel Barnes (born November 7, 1972),[1] also known professionally as C. D. Barnes, C. B. Barnes and C...

In Spanje worden sommige snelwegen geëxploiteerd door een concessiehouder, voor deze snelwegen dient er tol betaald te worden. Sommige concessiehouders zijn eigendom van meerdere bedrijven, vaak bouwbedrijven of banken. De looptijd en de voorwaarden van de concessies worden bepaald door de overheid die de snelweg in concessie gegeven heeft, dit kan zowel de centrale overheid zijn die het netwerk van staatssnelwegen beheert als een autonome gemeenschap. De grote meerderheid van de tolwegen ma...

اضغط هنا للاطلاع على كيفية قراءة التصنيف أيل بربري حالة الحفظ أنواع قريبة من خطر الانقراض المرتبة التصنيفية نويع[1] التصنيف العلمي المملكة: الحيوانات الشعبة: الحبليات العمارة: الثدييات الرتبة: مزدوجات الأصابع الفصيلة: الأيليات الجنس: أيل النوع: أيل أحمر النويع: أيل �...

Салукі Салукі Походження Середній Схід Інші назви перський хорт Характеристики Зріст пси 58—71 см,суки: трохи менше Зріст самців пси 58—71 см Зріст самиць суки: трохи менше Тривалість життя 12—14 років Класифікація МКФ: Група Група 10. Хорти Секція Секція 1. Довгошерсті та з па�...
An Carassai usa ka comune ha lalawigan han Ascoli Piceno ha rehiyon han Marche ha nasod han Italya. Usa ka turók ini nga barasahon. Dako it imo maibubulig ha Wikipedia pinaagi han pagparabong hini. khlMarche · Mga comune han Ascoli PicenoAcquasanta Terme · Acquaviva Picena · Appignano del Tronto · Arquata del Tronto · Ascoli Piceno · Carassai · Castel di Lama · Castignano · Castorano · Colli del Tronto · Comunanza · Cossignano · Cupra Marittima · Folignano · Force ·...

For the contract bridge method, see Vacant Places. 1st episode of the 3rd season of Fargo The Law of Vacant PlacesFargo episodeEpisode no.Season 3Episode 1Directed byNoah HawleyWritten byNoah HawleyProduced byLeslie CowanRegis KimbleChad OakesMichael FrislevFeatured musicJeff RussoProduction codeXFO03001Original air dateApril 19, 2017 (2017-04-19)Running time66 minutesGuest appearances Michael Stuhlbarg as Sy Feltz Scott Hylands as Ennis Stussy Scoot McNairy as Maurice LeF...

Bharain vehicle license plates Vehicle registration plates of Bahrain have the Flag of Bahrain and the country's name in Arabic and Latin script. Special vehicles such as diplomatic cars have a colored bar in the upper section of the license plate without the flag. License plates for private vehicle owners are blue with a white background. In 2010, Bahrain switched to the version which is in use today.[1] The international vehicle registration code for Bahrain is BRN. Types of license...

لونا 2 المشغل إنرجيا المصنع إنرجيا[1] تاريخ الإطلاق 12 سبتمبر 1959[2] موقع الإطلاق منصة جاجارين[2]، ومركز بايكونور الفضائي تاريخ الهبوط 14 سبتمبر 1959[3][4] لونا 3 تعديل مصدري - تعديل لونا 2 (بالروسية: Луна-2) المسبار الثاني الذي أطلق
Mixed relay at the Biathlon World Championships 2016VenueOslo, NorwayDate3 MarchCompetitors100 from 25 nationsTeams25Winning time1:14:01.0Medalists Anaïs BescondMarie Dorin HabertQuentin Fillon MailletMartin Fourcade France Franziska PreußFranziska HildebrandArnd PeifferSimon Schempp Germany Marte OlsbuTiril EckhoffJohannes Thingnes BøTarjei Bø Norway← 20152017 → Biathlon at the 2016 World C...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Unnamable film – news · newspapers · books · scholar · JSTOR (September 2015) (Learn how and when to remove this template message) 1988 American filmThe UnnamableRelease posterDirected byJean-Paul OuelletteScreenplay byJean-Paul OuelletteBased onThe Un...

2017 single by Gloc-9 featuring Mike LuisIce TubigSingle by Gloc-9 featuring Mike Luisfrom the album Rotonda ReleasedAugust 11, 2017Recorded2017GenreHip hopLength3:57LabelUniversal Records PhilippinesSongwriter(s)Aristotle Pollisco Ice Tubig is a single by Filipino rapper and songwriter Gloc-9 featuring Mike Luis. The song was set to be released in July 2017[1] but eventually moved a month later. It will be part of his five-track EP entitled Rotonda under Universal Records Philippines...

Bogota Borough Ubicación en el condado de Bergen en Nueva JerseyUbicación de Nueva Jersey en EE. UU.Coordenadas 40°52′27″N 74°01′47″O / 40.8743, -74.0297Entidad Borough • País Estados Unidos • Estado Nueva Jersey • Condado BergenAlcalde Pat McHaleFundación 14 de noviembre de 1894Superficie • Total 2.1 km² • Tierra 2 km² • Agua (7.32%) 0.2 km²Altitud • Media 17 m s. n. m.Población&...
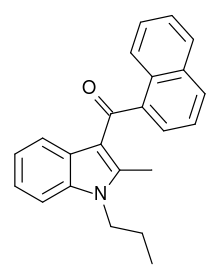
Chemical compound JWH-015Legal statusLegal status CA: Schedule II DE: Anlage II (Authorized trade only, not prescriptible) UK: Class B US: Schedule I Identifiers IUPAC name (2-Methyl-1-propyl-1H-indol-3-yl)-1-naphthalenylmethanone CAS Number155471-08-2 YPubChem CID4273754IUPHAR/BPS5558ChemSpider3480676 NUNIIW4FL204T10CompTox Dashboard (EPA)DTXSID60165902 ECHA InfoCard100.161.912 Chemical and physical dataFormulaC23H21NOMolar mass327.427 g·mol−13D model (J...

Asian Games medalists Main article: Handball at the Asian Games This is the complete list of Asian Games medalists in handball from 1982 to 2018. Men Games Gold Silver Bronze 1982 New Delhi China (CHN)Cai JianguoDeng ShanjunGao ZhongxinHu WeidongJin BailanLi YingcaiMin YueSong AnwenSun TieWang XiongWang YuetingWei HepingWu MingqunXie Jiyong Japan (JPN)Seimei GamoTakashi IkenoueYasuo IkomaEiichi InoHidetada ItoKoji MatsuiToru NaganoKiyoshi NishiyamaTakahiro OhataKoji Sait...

FN SLP 类型半自動戰術霰彈槍原产地 比利時生产历史研发者國營埃斯塔勒(Fabrique Nationale de Herstal,FN)研发日期2008年生产商國營赫斯塔爾(Fabrique Nationale de Herstal,FN)单位成本 SLP標準型:US$1,000 SLP Mark I型:US$1,324 生产日期2008年—衍生型 SLP標準型[1] SLP Mark I型[2] SLP戰術型[3] SLP Mark I戰術型[4] SLP Mark I比賽型[5] 基本规格重量空槍: SLP標準型�...

Canadian-American actress and author Beverly SassoonBeverly Adams in trailer for How to Stuff a Wild Bikini (1965)Born1944 or 1945 (age 78–79)Edmonton, Alberta, CanadaOther namesBeverly SassoonOccupation(s)Actress, authorYears active1963–1999Spouses Vidal Sassoon (m. 1967; div. 1980) Antonio Migoni (annulled) Philip Neal Children4, including Catya Sassoon Beverly Sassoon (born 1944...

Maltese English-language newspaper This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's notability guidelines for products and services. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notabilit...
The Book of Discipline refers to two works regulative of ecclesiastical order in the Church of Scotland, known as The First Book of Discipline (1560) and The Second Book of Discipline (1578), drawn up and printed in the Scottish Reformation. The first was drafted by a committee of six Johns, including leading reformer John Knox. It set out a system of Presbyterian polity on the Geneva model, but the lack of funds meant its programme of clerical organisation and education was largely abandoned...

Women's hammer throw at the 2018 World U20 ChampionshipsVenueRatina StadiumDates12 July (qualification)14 July (final)Competitors32 from 24 nationsWinning distance64.90 mMedalists Camryn Rogers Canada Alyssa Wilson United States Yaritza Martínez Cuba← 20162021 → Events at the2018 World ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen3000 mwomen5000 mmenwome...

Michel DuchaussoyDuchaussoy in 2008Lahir(1938-11-29)29 November 1938Valenciennes, PrancisMeninggal13 Maret 2012(2012-03-13) (umur 73)Paris, PrancisPekerjaanPemeranTahun aktif1962-2012 Michel René Jacques Duchaussoy (29 November 1938 – 13 Maret 2012)[1] adalah seorang pemeran film asal Prancis. Ia tampil dalam lebih dari 130 film antara 1962 dan 2012. Filmografi pilihan The Killing Game (1967) The Unfaithful Wife (1968) This Man Must Die (1969) Bye bye, Barba...


