![]() –ü–Ľ–ĺ—Č–į —Ä–ĺ–∂–Ķ–≤–ĺ–≥–ĺ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į —Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –ĺ–ī–Ĺ—É —Ā—Ć–ĺ–ľ—É –Ņ–Ľ–ĺ—Č—Ė –≤–Ķ–Ľ–ł–ļ–ĺ–≥–ĺ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į ABC.
–ü–Ľ–ĺ—Č–į —Ä–ĺ–∂–Ķ–≤–ĺ–≥–ĺ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į —Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –ĺ–ī–Ĺ—É —Ā—Ć–ĺ–ľ—É –Ņ–Ľ–ĺ—Č—Ė –≤–Ķ–Ľ–ł–ļ–ĺ–≥–ĺ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į ABC.
–£ –Ķ–≤–ļ–Ľ—Ė–ī–ĺ–≤—Ė–Ļ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä—Ė—ó —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ ABC –ľ—Ė—Ā—ā–ł—ā—Ć —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ, –Ņ–Ľ–ĺ—Č–į —Ź–ļ–ĺ–≥–ĺ —Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –ĺ–ī–Ĺ—É —Ā—Ć–ĺ–ľ—É –Ņ–Ľ–ĺ—Č—Ė ABC, —Ź–ļ–ł–Ļ –ľ–ĺ–∂–Ĺ–į –Ņ–ĺ–Ī—É–ī—É–≤–į—ā–ł —ā–į–ļ: —Ā—ā–ĺ—Ä–ĺ–Ĺ–ł —Ü—Ć–ĺ–≥–ĺ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į –Ľ–Ķ–∂–į—ā—Ć –Ĺ–į –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź—Ö p, q, r, –ī–Ķ
- p –∑'—Ē–ī–Ĺ—É—Ē A –∑ —ā–ĺ—á–ļ–ĺ—é –Ĺ–į BC, –≤—Ė–ī–ī–į–Ľ–Ķ–Ĺ–ĺ—é –≤—Ė–ī B –Ĺ–į —ā—Ä–Ķ—ā–ł–Ĺ—É –≤—Ė–ī—Ā—ā–į–Ĺ—Ė –≤—Ė–ī B –ī–ĺ C,
- q –∑'—Ē–ī–Ĺ—É—Ē B –∑ —ā–ĺ—á–ļ–ĺ—é –Ĺ–į CA, –≤—Ė–ī–ī–į–Ľ–Ķ–Ĺ–ĺ—é –≤—Ė–ī C –Ĺ–į —ā—Ä–Ķ—ā–ł–Ĺ—É –≤—Ė–ī—Ā—ā–į–Ĺ—Ė –≤—Ė–ī C –ī–ĺ A,
- r –∑'—Ē–ī–Ĺ—É—Ē C –∑ —ā–ĺ—á–ļ–ĺ—é –Ĺ–į AB, –≤—Ė–ī–ī–į–Ľ–Ķ–Ĺ–ĺ—é –≤—Ė–ī A –Ĺ–į —ā—Ä–Ķ—ā–ł–Ĺ—É –≤—Ė–ī—Ā—ā–į–Ĺ—Ė –≤—Ė–ī A –ī–ĺ B.
–Ē–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ—Ź —Ä—Ė–≤–Ĺ–ĺ—Ā—ā—Ė –Ņ–Ľ–ĺ—Č—Ė –ĺ–ī–Ĺ—Ė–Ļ —Ā—Ć–ĺ–ľ—Ė–Ļ –Ņ–Ľ–ĺ—Č—Ė –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–ĺ–≥–ĺ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į –≤–ł–Ņ–Ľ–ł–≤–į—Ē –∑ –Ņ–ĺ–Ī—É–ī–ĺ–≤–ł —ą–Ķ—Ā—ā–ł –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł—Ö –Ņ—Ä—Ź–ľ–ł—Ö:
- –ī–≤—Ė –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ—Ė p, –ĺ–ī–Ĺ–į —á–Ķ—Ä–Ķ–∑ C, —Ė–Ĺ—ą–į —á–Ķ—Ä–Ķ–∑ q.r
- –ī–≤—Ė –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ—Ė q, –ĺ–ī–Ĺ–į —á–Ķ—Ä–Ķ–∑ A, —Ė–Ĺ—ą–į —á–Ķ—Ä–Ķ–∑ r.p
- –ī–≤—Ė –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ—Ė r, –ĺ–ī–Ĺ–į —á–Ķ—Ä–Ķ–∑ B, —Ė–Ĺ—ą–į —á–Ķ—Ä–Ķ–∑ p.q.
–ď—É–≥–ĺ –®—ā–Ķ–Ļ–Ĺ–≥–į—É–∑ –∑–į–Ņ—Ä–ĺ–Ņ–ĺ–Ĺ—É–≤–į–≤ –≤—Ė–ī–Ī–ł—ā–ł (—Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ł–Ļ) —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ –∑—Ė —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ–ł –Ĺ–į p, q, r –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –Ļ–ĺ–≥–ĺ —Ā—ā–ĺ—Ä—Ė–Ĺ —Ė –≤–Ķ—Ä—ą–ł–Ĺ.[1] –¶—Ė —ą—Ė—Ā—ā—Ć –ī–ĺ–ī–į—ā–ļ–ĺ–≤–ł—Ö —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤ —á–į—Ā—ā–ļ–ĺ–≤–ĺ –Ņ–ĺ–ļ—Ä–ł–≤–į—é—ā—Ć ABC —Ė –∑–į–Ľ–ł—ą–į—é—ā—Ć —ą—Ė—Ā—ā—Ć —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤, —Č–ĺ ¬ę–∑–≤–ł—Ā–į—é—ā—ƬĽ –∑–į –ľ–Ķ–∂—Ė ABC. –ó–≤–į–∂–į—é—á–ł –Ĺ–į –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ—Ė—Ā—ā—Ć –Ņ—Ė–ī —á–į—Ā –Ņ–ĺ–Ī—É–ī–ĺ–≤–ł (—Ź–ļ –Ņ–ĺ–ļ–į–∑–į–≤ –ú–į—Ä—ā—Ė–Ĺ –ď–į—Ä–ī–Ĺ–Ķ—Ä —É –ĺ–Ĺ-–Ľ–į–Ļ–Ĺ –∂—É—Ä–Ĺ–į–Ľ—Ė –Ē–∂–Ķ–Ļ–ľ—Ā–į –†–Ķ–Ĺ–ī—Ė), –ĺ—á–Ķ–≤–ł–ī–Ĺ—Ė –Ņ–į—Ä–Ĺ—Ė –∑–Ī—Ė–≥–ł ¬ę–∑–≤–ł—Ā–į—é—á–ł—Ö¬Ľ —ā–į –≤—Ė–ī—Ā—É—ā–Ĺ—Ė—Ö —á–į—Ā—ā–ł–Ĺ –ź–í–°. –Į–ļ –≤–ł–ī–Ĺ–ĺ –∑ –≥—Ä–į—Ą—Ė—á–Ĺ–ĺ–≥–ĺ —Ä–ĺ–∑–≤'—Ź–∑–ļ—É, —ą—Ė—Ā—ā—Ć –≤—Ė–ī–Ī–ł—ā–ł—Ö —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤ —Ä–į–∑–ĺ–ľ –∑ –ĺ—Ä–ł–≥—Ė–Ĺ–į–Ľ–ĺ–ľ –ī–ĺ—Ä—Ė–≤–Ĺ—é—é—ā—Ć —Ü—Ė–Ľ–ĺ–ľ—É —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ—É ABC.[2]
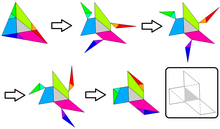 –ó–Ī—Ė–≥ –ī–ĺ–≤–∂–ł–Ĺ —Ā—ā–ĺ—Ä—Ė–Ĺ –ī–ĺ–∑–≤–ĺ–Ľ—Ź—Ē –ĺ–Ī–Ķ—Ä—ā–į—ā–ł –≤–ł–Ī—Ä–į–Ĺ—Ė —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–ł, —É—ā–≤–ĺ—Ä—é—é—á–ł —ā—Ä–ł –Ņ–į—Ä–į–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ł —Ä—Ė–≤–Ĺ–ĺ—ó –Ņ–Ľ–ĺ—Č—Ė, —Ź–ļ—Ė –ī—Ė–Ľ—Ź—ā—Ć—Ā—Ź –Ĺ–į–≤–Ņ—Ė–Ľ –Ĺ–į —ą—Ė—Ā—ā—Ć —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤ –ĺ–ī–Ĺ–į–ļ–ĺ–≤–ĺ–≥–ĺ —Ä–ĺ–∑–ľ—Ė—Ä—É –∑ –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–ł–ľ –≤–Ĺ—É—ā—Ä—Ė—ą–Ĺ—Ė–ľ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–ĺ–ľ.
–ó–Ī—Ė–≥ –ī–ĺ–≤–∂–ł–Ĺ —Ā—ā–ĺ—Ä—Ė–Ĺ –ī–ĺ–∑–≤–ĺ–Ľ—Ź—Ē –ĺ–Ī–Ķ—Ä—ā–į—ā–ł –≤–ł–Ī—Ä–į–Ĺ—Ė —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–ł, —É—ā–≤–ĺ—Ä—é—é—á–ł —ā—Ä–ł –Ņ–į—Ä–į–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ł —Ä—Ė–≤–Ĺ–ĺ—ó –Ņ–Ľ–ĺ—Č—Ė, —Ź–ļ—Ė –ī—Ė–Ľ—Ź—ā—Ć—Ā—Ź –Ĺ–į–≤–Ņ—Ė–Ľ –Ĺ–į —ą—Ė—Ā—ā—Ć —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤ –ĺ–ī–Ĺ–į–ļ–ĺ–≤–ĺ–≥–ĺ —Ä–ĺ–∑–ľ—Ė—Ä—É –∑ –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–ł–ľ –≤–Ĺ—É—ā—Ä—Ė—ą–Ĺ—Ė–ľ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–ĺ–ľ.
1859 —Ä–ĺ–ļ—É —Ü—é –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ—É –Ņ–ĺ–Ī—É–ī–ĺ–≤—É —ā–į –ĺ–Ī—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—Ź –Ņ–Ľ–ĺ—Č—Ė –Ĺ–į–≤—Ė–≤ —É —Ā–≤–ĺ—Ē–ľ—É –Ņ—Ė–ī—Ä—É—á–Ĺ–ł–ļ—É –∑ –Ķ–≤–ļ–Ľ—Ė–ī–ĺ–≤–ĺ—ó –≥–Ķ–ĺ–ľ–Ķ—ā—Ä—Ė—ó –†–ĺ–Ī–Ķ—Ä—ā –ü–ĺ—ā—ā—Ā.[3]
–ó–į —Ā–Ľ–ĺ–≤–į–ľ–ł –ö—É–ļ–į —ā–į –í—É–ī–į (2004), —Ü–Ķ–Ļ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ —Ā–Ņ–į–Ĺ—ā–Ķ–Ľ–ł—á–ł–≤ –†—Ė—á–į—Ä–ī–į –§–Ķ–Ļ–Ĺ–ľ–į–Ĺ–į –Ņ—Ė–ī —á–į—Ā –ĺ–Ī—Ė–ī–Ĺ—Ć–ĺ—ó —Ä–ĺ–∑–ľ–ĺ–≤–ł; –≤–ĺ–Ĺ–ł –Ĺ–į–ī–į—é—ā—Ć —á–ĺ—ā–ł—Ä–ł —Ä—Ė–∑–Ĺ—Ė –ī–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ—Ź.[4]
–ó–į–≥–į–Ľ—Ć–Ĺ—Ė—ą–ł–Ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –≤—Ė–ī–ĺ–ľ–ł–Ļ —Ź–ļ —ā–Ķ–ĺ—Ä–Ķ–ľ–į –†–į—É—Ā–į.
–ü—Ä–ł–ľ—Ė—ā–ļ–ł
–õ—Ė—ā–Ķ—Ä–į—ā—É—Ä–į