–Р–≤—В–Њ–Љ–∞—В–Є–Ј–Њ–≤–∞–љ–µ –Љ—Ц—А–Ї—Г–≤–∞–љ–љ—П
|
Read other articles:

Stasiun Kawunganten Stasiun Kawunganten, 2020LokasiKawunganten Lor, Kawunganten, Cilacap, Jawa Tengah 53253IndonesiaKetinggian+15 mOperatorKereta Api IndonesiaDaerah Operasi V PurwokertoLetak dari pangkalkm 363+471 lintas Bogor-Bandung-Banjar-Kutoarjo-Yogyakarta[1]Jumlah peron2 (satu peron sisi yang agak rendah dan satu peron pulau yang agak tinggi)Jumlah jalur3 (jalur 2: sepur lurus)Informasi lainKode stasiunKWG2011[2]KlasifikasiIII/kecil[2]Operasi layanan Hanya untuk...
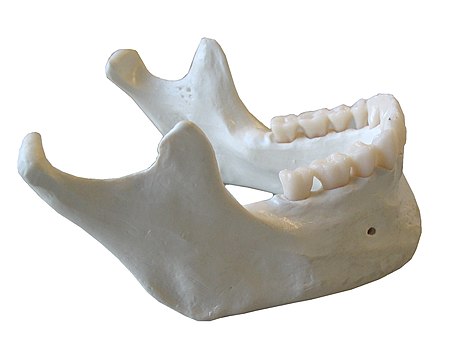
ЎІўДўБўОўГўПўС ЎІўДЎ≥ўПўСўБўДўРўКўС ЎІўДЎІЎ≥ўЕ ЎІўДЎєўДўЕўКmandibula ЎєЎЄўЕ ЎІўДўБўГ ЎІўДЎ≥ўБўДўКўС ЎІўДЎђўЕЎђўЕЎ© ЎІўДЎ®ЎіЎ±ўКўСЎ©ЎМ ўИўКЎЄўЗЎ± ЎєЎЄўЕ ЎІўДўБўГ ЎІўДЎ≥ўБўДўРўКўС Ў®ЎІўДўДўИўЖ ЎІўДЎ£Ў±ЎђўИЎІўЖўК Ў£Ў≥ўБўД ЎІўДЎµўИЎ±Ў©.ЎІўДЎђўЕЎђўЕЎ© ЎІўДЎ®ЎіЎ±ўКўСЎ©ЎМ ўИўКЎЄўЗЎ± ЎєЎЄўЕ ЎІўДўБўГ ЎІўДЎ≥ўБўДўРўКўС Ў®ЎІўДўДўИўЖ ЎІўДЎ£Ў±ЎђўИЎІўЖўК Ў£Ў≥ўБўД ЎІўДЎµўИЎ±Ў©. Ў™ўБЎІЎµўКўД Ў≥ўДўБ ЎІўДўВўИЎ≥ ЎІўДЎ®ўДЎєўИўЕўКЎ© ЎІўДЎ£ўИўДўЙ[1] ўЖўИЎє ўЕўЖ ЎєЎЄўЕЎМ ўИўГўКЎІўЖ Ў™ЎіЎ±ўКЎ≠ўК ўЕЎєўКў...

–Э–∞—Ж—Ц–Њ–љ–∞ћБ–ї—М–љ—Ц —А–∞–є–ЊћБ–љ–Є вАФ –∞–і–Љ—Ц–љ—Ц—Б—В—А–∞—В–Є–≤–љ–Њ-—В–µ—А–Є—В–Њ—А—Ц–∞–ї—М–љ—Ц –Њ–і–Є–љ–Є—Ж—Ц –≤ –°–†–°–†, —Б—В–≤–Њ—А–µ–љ—Ц –і–ї—П –Ј–∞–і–Њ–≤–Њ–ї–µ–љ–љ—П –µ—В–љ–Њ–Ї—Г–ї—М—В—Г—А–љ–Є—Е –њ–Њ—В—А–µ–± –Љ—Ц—Б—Ж–µ–≤–Њ–≥–Њ –љ–∞—Б–µ–ї–µ–љ–љ—П, —Й–Њ —Б—В–∞–љ–Њ–≤–Є–ї–Њ –≤–∞–≥–Њ–Љ–Є–є –≤—Ц–і—Б–Њ—В–Њ–Ї –Љ–µ—И–Ї–∞–љ—Ж—Ц–≤ —А–∞–є–Њ–љ—Г —Ц –±—Г–ї–Њ –≤—Ц–і–Љ—Ц–љ–љ–Є–Љ –≤—Ц–і —В–Є—В—Г–ї—М–љ–Њ–≥–Њ –љ–∞—А–Њ–і—Г –њ–µ–≤–љ–Њ—Ч —А–µ—Б–њ—Г–±–ї—Ц–Ї–Є. –І–∞—Б—В–Њ –њ–µ–≤–љ—Ц –љ–∞—Ж—Ц–Њ–љ–∞–ї—...

The article is about the list of state highways in the Indian state of Andhra Pradesh. The state has a total of 14,722 km (9,148 mi) of State Highways and they account for 29% of the total roads in the state. SH 31 is the longest State Highway in Andhra Pradesh. The new state highways are recently added and new numbering system is given for state highways to improve infrastructure and connectivity.[1][2] S.No State Highway No. Route Districts connecting 1 NH167AG Pid...

American online service for haulage companies This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (August 2017) (Learn how and when to remove this template message) DAT Freight & AnalyticsTypeSubsidiary of Roper TechnologiesIndustryTruckload shippingFounded1978HeadquartersBeaverton, Oregon, United StatesProductsT...

–Ф–ґ–Њ–≤–∞–љ–љ—Ц –У—А–∞–і–µ–љ—Ц–≥–Њ —Ц—В–∞–ї. Giovanni Gradenigo –Ф–ґ–Њ–≤–∞–љ–љ—Ц –У—А–∞–і–µ–љ—Ц–≥–Њ56-–є –і–Њ–ґ–Я–Њ—З–∞—В–Њ–Ї –њ—А–∞–≤–ї—Ц–љ–љ—П: 1355 —А—Ц–Ї–Ъ—Ц–љ–µ—Ж—М –њ—А–∞–≤–ї—Ц–љ–љ—П: 1356 —А—Ц–Ї –Я–Њ–њ–µ—А–µ–і–љ–Є–Ї: –Ь–∞—А–Є–љ–Њ –§–∞–ї—М—Ф—А–Њ–Э–∞—Б—В—Г–њ–љ–Є–Ї: –Ф–ґ–Њ–≤–∞–љ–љ—Ц –Ф–µ–ї—М—Д—Ц–љ–Њ –Ф–∞—В–∞ –љ–∞—А–Њ–і–ґ–µ–љ–љ—П: 1273–Ь—Ц—Б—Ж–µ –љ–∞—А–Њ–і–ґ–µ–љ–љ—П: –Т–µ–љ–µ—Ж—Ц—П–Ъ—А–∞—Ч–љ–∞: –Т–µ–љ–µ—Ж—Ц–є—Б—М–Ї–∞ —А–µ—Б–њ—Г–±–ї—Ц–Ї–∞–Ф–∞—В–∞ —Б–Љ–µ—А—В—Ц: 8 —Б–µ—А–њ–љ—П 1356–Ь

Comics character SolarisSolaris, as it appeared on the cover of DC One Million #3 (September 1998), art by Val Semeiks.Publication informationPublisherDC ComicsFirst appearanceDC One Million #1 (1998)Created byGrant MorrisonIn-story informationAlter egoSolarisSpeciesSentient artificial starTeam affiliationsSuperman dynastyPancosmic Justice JihadAbilitiesArtificial intelligence, energy control (solar radiation manipulation) Solaris (also known as Solaris the Tyrant Sun) is a DC Comics supervil...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2016) (Learn how and when to remove this template message) This article relies largely or entirely on a single source. Relevant discussion may be found o...

2008 study published by the World Bank and the Food and Agriculture Organization The Sunken Billions: The Economic Justification for Fisheries Reform AuthorRagnar Arnason, Kieran Kelleher and Rolf WillmannLanguageEnglishSubjectWorld fisheriesPublisherJoint publication by the World Bank and the FAOPublication date2008Media typePrintISBN978-0-8213-7790-1OCLC297146442Dewey Decimal338.3/727 22LC ClassSH328 .S79 2009 The Sunken Billions is a study jointly published in 2008 by the World B...

State of Malaysia Negri Sembilan and Darul Khusus redirect here. For other uses, see Negri (disambiguation). For Malaysian states (negeri) in general, see States and federal territories of Malaysia. For the Egyptian city, see Khusus. StateNegeri Sembilan Nogori SombilanStateNegeri Sembilan Darul KhususўЖЁҐЎ±ўК Ў≥ўЕЎ®ўКўДўЖ ЎѓЎІЎ± ЎІўДЎЃЎµўИЎµOther transcription(s) вАҐ JawiўЖЁҐЎ±ўК Ў≥ўЕЎ®ўКўДўЖ вАҐ Chineseж£ЃзЊОеЕ∞ (Simplified)ж£ЃзЊОиШ≠ (Traditional) ...

Wendell and Carol Race (his oldest daughter) Wendell E. Reed was an aircraft engineer noted primarily for inventing the engine microjet controller (EMC) (U.S. Patent 2,726,507, U.S. Patent 2,981,058), for which he was awarded the Wright Brothers Medal in 1955.[1][2][3] Reed's experiences in the USAAF piloting the B-25 kindled a lifelong interest in flight and he later completed his degree at University of Wisconsin in Mechanical Engineering.[4] He subsequently ...

American musician This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Soozie Tyrell вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (August 2010) (Learn how and when to remove this template message) S...
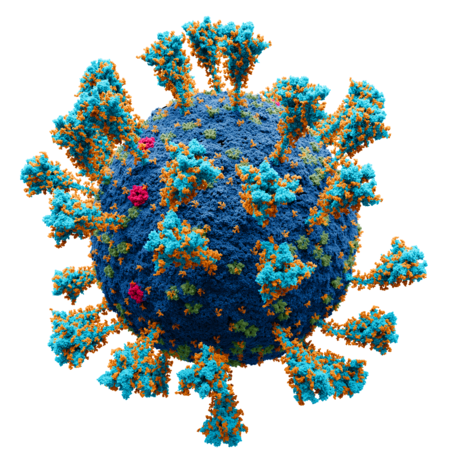
ЎІўДЎ™Ў≥ўДЎ≥ўД ЎІўДЎ≤ўЕўЖўК ЎђЎІЎ¶Ў≠Ў© ўБўКЎ±ўИЎ≥ ўГўИЎ±ўИўЖЎІ 2019вАУ20 ўБўК ўЕЎІЎ±Ў≥ 2020ўЕЎєўДўИўЕЎІЎ™ ЎєЎІўЕЎ©ЎђЎ≤Ў° ўЕўЖ ЎІўДЎЃЎЈ ЎІўДЎ≤ўЕўЖўК ўДЎђЎІЎ¶Ў≠Ў© ўБўКЎ±ўИЎ≥ ўГўИЎ±ўИўЖЎІ 2019-20 ЎђЎІўЖЎ® ўЕўЖ ЎђўИЎІўЖЎ® ЎђЎІЎ¶Ў≠Ў© ўБўКЎ±ўИЎ≥ ўГўИЎ±ўИўЖЎІ ЎІўДўЕўИЎґўИЎє ЎІўДЎ±Ў¶ўКЎ≥ ЎђЎІЎ¶Ў≠Ў© ўБўКЎ±ўИЎ≥ ўГўИЎ±ўИўЖЎІўЕЎІЎ±Ў≥ 2020 Ў®Ў™ЎІЎ±ўКЎЃ ўЕЎІЎ±Ў≥ 2020 Ў™ЎІЎ±ўКЎЃ ЎІўДЎ®ЎѓЎ° 1 ўЕЎІЎ±Ў≥ 2020 Ў™ЎІЎ±ўКЎЃ ЎІўДЎІўЖЎ™ўЗЎІЎ° 31 ўЕЎІЎ±Ў≥ 2020 ЎІўДЎ™Ў≥ўДЎ≥ўД ЎІўДЎ≤ўЕўЖўК ЎђЎІЎ¶Ў≠Ў© ўБўКЎ±ўИЎ≥ ўГўИЎ±ўИ...

Islamic leadership position, difference in shia Islam and sunni Islam For other uses, see Imam (disambiguation). Not to be confused with Iman or Imamah. Mughal Imams in discourse Part of a series on IslamUsul al-Fiqh Fiqh Ijazah Ijma Ijtihad Ikhtilaf Istihlal Istihsan Istishab Madhhab Madrasah Maslaha Qiyas Taqlid Urf Ahkam Fard Mustahabb Halal Mubah Makruh Haram Baligh Batil Bid'ah Fahisha Fasiq Fitna Fasad Gunah Haya Islah Istighfar Hirabah Istishhad Jihad Qasd Sunnah Tafsir Taghut Taqiya T...

This article is about the 2000 film. For the Italian comune, see Urbania. 2000 American filmUrbaniaDirected byJon ShearPhilippe DenhamWritten byDaniel Reitz (play and screenplay)Jon Shear (screenplay)Produced byMark V. DziakJ. Todd HarrisStephanie GoldenStarringDan FuttermanPaige TurcoSamuel BallJosh HamiltonMatt KeeslarAlan CummingCinematographyShane F. KellyPeter KonczalRonnie DennisEdited byRandy BrickerEd MarxMusic byMarc Anthony ThompsonDistributed byLions Gate FilmsRelease dates January...

Claudia Gravy (born 12 May 1945) is a Spanish nationalized actress born as Marie-Claude Perin in Boma, Democratic Republic of the Congo when it was the Belgian Congo. Claudia GravyGravy in 2018Born (1945-05-12) 12 May 1945 (age 78)Boma, Belgian CongoOther namesClaudia GraviOccupationActor Career Claudia has lived in Madrid since 1965, when she made her debut in the cinema with Fernando Fernán Gómez's adaption of Miguel Mihura's work, Ninette y un señor de Murcia. During the follo...

2004 single by McFly ObviouslyOne of artwork variantsSingle by McFlyfrom the album Room on the 3rd Floor B-sideGet Over YouReleased21 June 2004 (2004-06-21)[1]Genre Pop rock acoustic rock[2] Length3:18LabelIslandSongwriter(s) James Bourne Tom Fletcher Danny Jones Producer(s)Hugh PadghamMcFly singles chronology 5 Colours in Her Hair (2004) Obviously (2004) That Girl (2004) Music videoObviously on YouTube Obviously is a song by English pop rock band McFly. It was ...

Clasificaci√≥n de CAF para la Copa Mundial de F√Їtbol de 1978 1976-1977 Fecha 7 de marzo de 197611 de diciembre de 1977 Cantidad de equipos 26 Equipos clasificados TUN T√Їnez Partidos 42 Goles anotados 118 (2,81 por partido) Goleador Mahmoud El Khatib (6 goles) En la fase de clasificaci√≥n para la Copa Mundial de F√Їtbol de 1978 celebrado en Argentina, la CAF dispon√≠a de una plaza (de las 16 totales del mundial). Para asignar esta plaza, a la que optaban un total de 26 equipos...

Type of percussion mallet This article is about the musical tool. For other uses, see Drumstick (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Drum stick вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (June 2012) (Learn how and when to remove this template message) A selection of Nick Mason...

Class of natural numbers In mathematics, a superabundant number is a certain kind of natural number. A natural number n is called superabundant precisely when, for all m < n: σ ( m ) m < σ ( n ) n {\displaystyle {\frac {\sigma (m)}{m}}<{\frac {\sigma (n)}{n}}} where ѕГ denotes the sum-of-divisors function (i.e., the sum of all positive divisors of n, including n itself). The first few superabundant numbers are 1, 2, 4, 6, 12, 24, 36, 48, 60, 120, ... (sequence A004394 i...
