Кутова роздільність (теорія графів)
|
Read other articles:

SexagesimaLiturgical colorVioletSignificancePreparation for LentDateSecond Sunday before Ash Wednesday (56 calendar days before Easter Sunday)2022 dateFebruary 202023 dateFebruary 122024 dateFebruary 42025 dateFebruary 23Related toShrovetide Liturgical seasons Pre-Christmas Advent (Western) Nativity Fast (Byzantine) Annunciation (Syriac) Christmas Epiphany Ordinary Time (Western) Pre-Lent Lent (Western) / Great Lent (Eastern) Paschal Triduum Easter Pentecost Ordi...

Glucogenina 1[1] Estructura de la glucogenina del músculo del conejo.Estructuras disponiblesPDB Buscar ortólogos: PDBe, RCSB Estructuras enzimáticasRCSB PDB, PDBe, PDBsum IdentificadoresSímbolos GYG1 (HGNC: 4699) GN1Identificadoresexternos OMIM: 603942 EBI: GYG1GeneCards: Gen GYG1UniProt: GYG1 Bases de datos de enzimasIntEnz: entrada en IntEnz BRENDA: entrada en BRENDA ExPASy: NiceZime view KEGG: entrada en KEEG PRIAM: perfil PRIAM ExplorEnz: entrada en Explor...

Penyuntingan Artikel oleh pengguna baru atau anonim untuk saat ini tidak diizinkan.Lihat kebijakan pelindungan dan log pelindungan untuk informasi selengkapnya. Jika Anda tidak dapat menyunting Artikel ini dan Anda ingin melakukannya, Anda dapat memohon permintaan penyuntingan, diskusikan perubahan yang ingin dilakukan di halaman pembicaraan, memohon untuk melepaskan pelindungan, masuk, atau buatlah sebuah akun. Jak TVPT Danapati Abinaya InvestamaJakarta Selatan, DKI JakartaIndonesiaSaluranDi...

2012 single by the Killers RunawaysSingle coverSingle by the Killersfrom the album Battle Born ReleasedJuly 17, 2012Recorded2011–2012Genre Heartland rock new wave Length4:04LabelIslandComposer(s)The KillersLyricist(s)Brandon FlowersProducer(s) Steve Lillywhite Brendan O'Brien The Killers The Killers singles chronology The Cowboys' Christmas Ball (2011) Runaways (2012) Miss Atomic Bomb (2012) Music videoRunaways on YouTube Runaways is a song by American rock band the Killers. It was released...

YaquiThe location of the Yaqui people in Sonora, Mexico when first encountered by the SpanishDaerah dengan populasi signifikan United States ( Arizona, California)11,324BahasaYaqui, English, SpanishAgamaIndigenous Religion, ChristianityKelompok etnik terkaitMayo Uto-Aztecan people Yaqui people, c. 1910 Yaqui atau Yoeme adalah nama suku atau orang-orang pribumi Amerika yang merupakan leluhur dari lembah Río Yaqui yaitu wilayah utara Meksiko, Arizona, dan California.[1]...

Keuskupan Puerto PlataDioecesis Portus ArgentariiDiócesis de Puerto PlataKatolik Catedral San Felipe ApóstolLokasiNegaraRepublik DominikaWilayahProvinsi Puerto PlataProvinsi gerejawiProvinsi Santiago de los CaballerosStatistikLuas2.700 km2 (1.000 sq mi)Populasi- Total- Katolik(per 2004)346.520338,560 (97.7%)Paroki31InformasiDenominasiKatolik RomaRitusRitus RomaPendirian16 Desember 1996 (26 tahun lalu)KatedralKatedral Santo Filipus RasulKepemimpinan kiniPau...
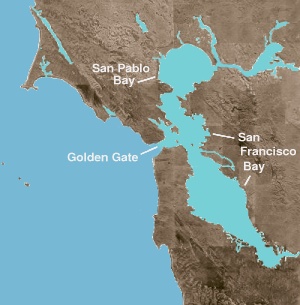
San Francisco Estuary The San Francisco Estuary together with the Sacramento–San Joaquin River Delta represents a highly altered ecosystem. The region has been heavily re-engineered to accommodate the needs of water delivery, shipping, agriculture, and most recently, suburban development. These needs have wrought direct changes in the movement of water and the nature of the landscape, and indirect changes from the introduction of non-native species. New species have altered the architecture...

11th century Icelandic explorer Thorfinn Karlsefni ThórdarsonStatue of Thorfinn by Einar JónssonBornc. 980–985Icelandic CommonwealthOccupationMerchant/Trader & ExplorerKnown forEarly exploration of VinlandPartnerGudrid ThorbjarnardóttirChildrenSnorri Thorfinnsson Part of a series on theNorse exploration ofNorth America Places Vinland Markland Helluland L'Anse aux Meadows Eastern Settlement Western Settlement Middle Settlement Gunnbjörn's skerries Great Ireland Tanfield Va...

1931 film Chinatown After DarkBilly Gilbert and Barbara Kent in Chinatown After DarkDirected byStuart PatonWritten byBetty BurbridgeProduced byRalph M. Like Cliff P. BroughtonCinematographyJules CronjagerEdited byByron RobinsonViola RoehlMusic byLee ZahlerProductioncompanyAction PicturesDistributed byMayfair PicturesRelease date October 15, 1931 (1931-10-15) Running time59 minutesCountryUnited StatesLanguageEnglish Chinatown After Dark is a 1931 American pre-Code drama film dir...

Mountain SorgschrofenSorgschrofen and ZinkenHighest pointElevation1,634.9 m (5,364 ft)metres above the Adriatic Prominence577 m (1,893 ft)Isolation3 km (1.9 mi) Coordinates47°33′21″N 10°27′15″E / 47.55583°N 10.45417°E / 47.55583; 10.45417GeographySorgschrofenLocation in Germany LocationBavaria, GermanyParent rangeAllgäu AlpsClimbingEasiest routeFrom Jungholz Sorgschrofen is a 1,635-metre-tall (5,364 ft) mou...

2019 StarCraft II World Championship Series Global Finals2019Tournament informationSportStarCraft IILocationAnaheim, CaliforniaAdministratorBlizzard EntertainmentVenue(s)Anaheim Convention CenterPurse$700,000Final positionsChampionPark Dark Ryung WooRunner-upRiccardo Reynor Romiti← 2018 The 2019 StarCraft II World Championship Series (WCS) is the 2019 edition of the StarCraft II World Championship Series, the top esports tournament circuit for StarCraft II.[1] The tournamen...

CreedCreed di Salt Lake City,Oktober 2009Informasi latar belakangNama lainNaked Toddler, Apostle's GreedAsalTallahassee, Florida, United StatesGenreHard rock, post-grungeTahun aktif1995 (1995)–2004, 2009–2012 (hiatus)LabelWind-upArtis terkaitAlter Bridge, ProjectedSitus webcreed.comAnggotaScott StappMark TremontiScott PhillipsBrian Marshall Creed adalah band rock alternatif yang terkenal pada akhir tahun 1990an dan awal 2000 di Amerika Serikat. Creed mengadaptasi lagu grunge rock alt...

Aeropuerto de Copenhague-Kastrup Københavns Lufthavn, Kastrup IATA: CPH OACI: EKCH FAA: LocalizaciónUbicación Tårnby, DinamarcaElevación 5Sirve a Copenhague Dinamarca Dinamarca Malmö Suecia SueciaDetalles del aeropuertoTipo PúblicoOperador Copenhagen Airports A/SEstadísticas (2021)Pasajeros 9 179 654Pasajeros nacionales 850 853Pasajeros internacionales 8 328 801Operaciones 109 925Pistas DirecciónLargoSuperficie04L/22R3600Asfalto04R/22L3300Asfalto12/...

Gli Archivi nazionali della Scozia (in inglese: National Archives of Scotland) sono l'archivio centrale dello stato della Scozia ed hanno sede a Edimburgo. Indice 1 Storia 2 Sedi 3 Patrimonio 4 Note 5 Collegamenti esterni Storia Il primo riferimento a un funzionario con la responsabilità di conservare i documenti risale al 1268, quando William of Dumfries risulta essere clerk of the rolls della cancelleria o chapel reale. Questa carica si trasformò più tardi in quella di Lord Clerk Registe...

Benzodiazepine drug BromazepamClinical dataTrade namesLexotan, Lexotanil, othersAHFS/Drugs.comMicromedex Detailed Consumer InformationRoutes ofadministrationBy mouthATC codeN05BA08 (WHO) Legal statusLegal status BR: Class B1 (Psychoactive drugs)[1] CA: Schedule IV DE: Prescription only (Anlage III for higher doses) UK: Class C US: Schedule IV Pharmacokinetic dataBioavailability84%MetabolismLiverElimination half-life12–20 hours (avg. 17hr)[2]...

Johnny Barbalinardo Lombardi Johnny Barbalinardo Lombardi (Toronto, 4 dicembre 1915 – Toronto, 18 marzo 2002) è stato un editore e imprenditore canadese, fondò una radio e fu un pioniere delle trasmissioni multiculturali in Canada. Figlio di immigrati italiani (di origine Pisticci, Basilicata), il padre si chiamava Leonardo Barbalinardo, (chi è cambiato il suo cognome in Lombardi)[1], era nato nella Little Italy di Toronto che allora corrispondeva al quartiere di College. Era un ...

Austrian physician Seligmann, Franz RomeoBorn30 June 1808MikulovDied15 September 1892(1892-09-15) (aged 84)ViennaOccupationAustrian doctor and medical historianAlma materUniversity of Vienna Abraham Romeo Seligmann better known as Franz Romeo Seligmann[1] (born 30 June 1808 in Nikolsburg, today Mikulov, in Moravia; died 15 September 1892 in Vienna), was an Austrian doctor and medical historian. Life Seligmann family grave at the Döbling Cemetery The son of doctor Isaak Seli...

この項目では、経済学上の市中銀行について説明しています。銀行制度上の商業銀行については「商業銀行」をご覧ください。 金融サービスに関連するテンプレート銀行業 銀行の種類 バルジ・ブラケット 中央 市中 信組 信用組合 カストディアン 輸出信用機関 投資 国立 ネット オフショア 郵便貯金 プライベート 公有(英語版) 貯蓄 貯蓄貸付 金融持株会社 信託 メ�...

Apache OpenOffice Apache OpenOffice 4.1.11 di LinuxTipegratis, aplikasi dan Paket aplikasi perkantoran BerdasarkaOpenOffice.org dan StarOffice Versi pertama30 April 2002 (2002-04-30)[1]Versi stabil 4.1.15 (22 Desember 2023) GenrePaket aplikasi perkantoranLisensiLGPL version 3[2] (OpenOffice.org 2 Beta 2 and earlier are dual-licensed under the SISSL and LGPL)[3] Apache License 2.0 (Apache OpenOffice 3.4 and later)[4]BahasaDaftar bahasa 99+ bahasa[5]...

Den här artikeln har skapats av Lsjbot, ett program (en robot) för automatisk redigering. (2013-06)Artikeln kan innehålla fakta- eller språkfel, eller ett märkligt urval av fakta, källor eller bilder. Mallen kan avlägsnas efter en kontroll av innehållet (vidare information) Ulochlaena hirta SystematikDomänEukaryoterEukaryotaRikeDjurAnimaliaStamLeddjurArthropodaUnderstamSexfotingarHexapodaKlassEgentliga insekterInsectaOrdningFjärilarLepidopteraÖverfamiljNoctuoideaFamiljNattflynNoct...













