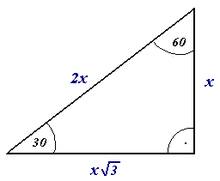
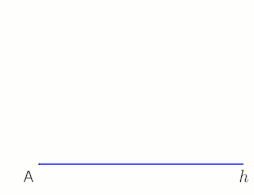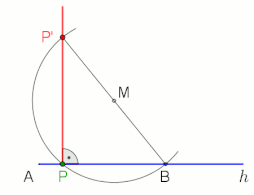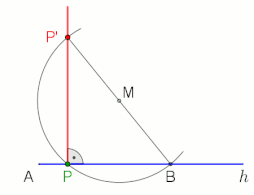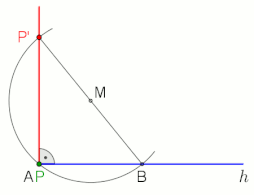
Dik açı
|
Read other articles:

La battaglia di Cajamarca, in un'incisione di Johann Theodor de Bry Miguel de Estete (Santo Domingo de la Calzada, 1495 – Lima, 1572 circa) è stato uno scrittore ed esploratore spagnolo, nonché uno dei primi conquistadores del Perù e redattore di una cronaca della conquista. Indice 1 Primi anni 2 La conquista del Perù 3 Vita di colonia 4 Le opere 5 Edizioni 6 Voci correlate 7 Altri progetti 8 Collegamenti esterni Primi anni Non sono pervenute notizie sulle esperienze giovanili di Miguel...

The facade of the Central Civic Library of Turin in 1929. Side towards Corso Palestro and Via BertrandiThe Biblioteca Civica Centrale of Turin, Italy, is a public library established in 1869.[1] It belongs to the Biblioteche Civiche Torinesi [it] library system. Among its collections are manuscripts produced by Vincenzo Gioberti. References ^ Biblioteca civica centrale. Anagrafe delle biblioteche italiane [it] (Registry of Italian Libraries) (in Italian). Ist...

Palacio Episcopal de Segovia Tipo palacio episcopalEstilo arquitectura del RenacimientoLocalización Segovia (España)Coordenadas 40°57′06″N 4°07′28″O / 40.951611111111, -4.1245277777778Construcción 1550Propietario Condado de Puñonrostro [editar datos en Wikidata] El Palacio Episcopal de Segovia es un edificio ubicado en el centro histórico de la ciudad española de Segovia. Fue residencia de los sucesivos obispos hasta 1969. Descripción El edificio, si...

England international rugby union player This article is about the English rugby union player. For the Wales rugby union player, see Eric Evans (rugby union, born 1894). Rugby playerEric EvansEric EvansDate of birth1 February 1921Place of birthDroylsden, Greater Manchester, EnglandDate of death12 January 1991(1991-01-12) (aged 69)SchoolAudenshaw Grammar SchoolOccupation(s)Sports TeacherRugby union careerPosition(s) HookerAmateur team(s)Years Team Apps (Points)1935-19391945-1963 Old Aldwi...

Тимчасовий основний закон про державну самостійність українських земель бувшої австро-угорської монархії, ухвалений Українською Національною Радою на засіданню 13 падолиста 1918 — історичний документ, прийнятий Українською Національною Радою 13 листопада 1918 року, що �...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: High Roller: The Stu Ungar Story – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this template message) 2003 American filmHigh Roller: The Stu Ungar StoryDirected byA. W. VidmerWritten byA. W. VidmerProduced byF.A. Miller...

Roman Catholic veneration of Mary Blessed VirginMaryMother of GodQueen of HeavenMother of the ChurchMediatrix of all gracesOur LadyBornSeptember 8 (Nativity of Mary)DiedThe Catholic Church teaches that, at the end of her natural life, she was assumed into heaven, body and soul (Assumption of Mary)Venerated inCatholic ChurchCanonizedPre-CongregationMajor shrineSanta Maria Maggiore, others (see Shrines to the Virgin Mary)FeastSee Marian feast daysAttributesBlue mantle, white veil, Immacula...

Avdo Spahić Avdo Spahic (2019) Personalia Geburtstag 12. Februar 1997 Geburtsort Berlin, Deutschland Größe 190 cm Position Tor Junioren Jahre Station 2005–2012 SFC Stern 1900 2012–2014 Tennis Borussia Berlin 2014–2015 Energie Cottbus Herren Jahre Station Spiele (Tore)1 2015–2016 Energie Cottbus II 8 (0) 2015–2019 Energie Cottbus 76 (0) 2019– 1. FC Kaiserslautern 46 (0) 1 Angegeben sind nur Ligaspiele. Stand: Saisonende 2022/23 Avdo Spahić (* 12. Februar 1997 in Berli...

British figure skater Stephanie MainStephanie Main at the British Championships in November 1995.Born (1976-09-20) 20 September 1976 (age 47)Edinburgh, ScotlandHeight1.57 m (5 ft 2 in)Figure skating careerCountry Great BritainCoachAlice Fell, Kathy Casey, Doug Leigh, Debbie Briggs, Kevin Bursey.Skating clubMurrayfieldBegan skating1979Retired2001 Stephanie Main (born 20 September 1976) is a British former competitive figure skater. She is a three-time British national ...

51.618326.754536Koordinaten: 51° 37′ 6″ N, 6° 45′ 16″ OStollbach (Naturschutzgebiet) Das Naturschutzgebiet Stollbach liegt auf dem Gebiet der Gemeinde Hünxe im Kreis Wesel in Nordrhein-Westfalen. Das aus zwei Teilflächen bestehende Gebiet erstreckt sich südwestlich des Kernortes von Hünxe und nördlich des Hünxer Ortsteils Bruckhausen zu beiden Seiten der A 3 und der Landesstraße L 1. Südwestlich des Gebietes, das vom Stollbach durchflosse...

Underemployed young adult in Japan This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2007) (Learn how and when to remove this template message) This article possibly contains original research. Please imp...

Brand of automotive surface care products Rain-XProduct typeAutomotive aftermarket in glass care; other car care: car washes, waxes, bug and tar removers, and headlight restoration kits.OwnerITW Global Brands, division of Illinois Tool Works (ITW)Introduced1972 (1972)Previous ownersPennzoil-Quaker State Company dba SOPUS ProductsTaglineOutsmart the elementsWebsiterainx.com Rain-X is a synthetic hydrophobic surface-applied product that causes water to bead up and run off surfaces, most co...

US American coin Franklin half dollarUnited StatesValue50 cents (0.50 US dollars)Mass12.50[1] gDiameter30.61[1] mm (1.21[1] in)Thickness1.8 mmEdgereeded[1]Composition 90% Ag 10% Cu[1] Silver0.36169[1] troy ozYears of minting1948–1963[1]Mint marksD, S on reverse, above yoke of bell and below letter E in STATES. Philadelphia Mint coins struck without mint mark.ObverseDesignBenjamin FranklinDesignerJohn R. Si...

Compilation of pre-Christian Celtic systems of timekeeping The Celtic calendar is a compilation of pre-Christian Celtic systems of timekeeping, including the Gaulish Coligny calendar, used by Celtic countries to define the beginning and length of the day, the week, the month, the seasons, quarter days, and festivals.[1] Continental Celtic calendar The Gaulish Coligny calendar is the oldest known Celtic solar-lunar ritual calendar. It was discovered in Coligny, France, and is now on di...

Major League Baseball franchise in Milwaukee, Wisconsin This article is about the present-day Major League Baseball team. For other uses, see Milwaukee Brewers (disambiguation). Milwaukee Brewers 2023 Milwaukee Brewers seasonEstablished in 1969Based in Milwaukee since 1970 Team logoCap insignia Major league affiliations National League (1998–present) Central Division (1998–present) American League (1969–1997) Central Division (1994–1997) East Division (1972–1993) West Division (1969...

Annual OTT film awards in India 2021 Filmfare OTT AwardsFilmfare OTT Awards 2021Awarded forExcellence in cinematic achievementsDate9 December 2021 (2021-12-09)VenueMumbaiCountryIndiaPresented byFilmfareFirst awarded19 December 2020 (2020-12-19)HighlightsMost awardsScam 1992: The Harshad Mehta Story (12)Best Drama SeriesScam 1992: The Harshad Mehta StoryBest Comedy SeriesGullakBest Film - Web OriginalsSerious MenBest Non - Fiction Original (Series)Bad Boy Billiona...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: George Clinton: The Mothership Connection – news · newspapers · books · scholar · JSTOR (August 2016) (Learn how and when to remove this template message) 1998 video by George Clinton; Parliament-FunkadelicGeorge Clinton: The Mothership ConnectionVideo by George Clinton;...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Soulfly discography – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this template message) Soulfly discographySoulfly performing in 2015Studio albums12Live albums2Compilation albums1Video albums1Music videos12EPs3Singles28...

Singaporean multinational supermarket company This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cold Storage supermarket – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this template message) Cold StorageTypePrivate (1903–1992) Subsidiary (1992–)IndustryRetailFou...

State agency of the Commonwealth of Massachusetts MDCR redirects here. For the airport with that ICAO code, see Cabo Rojo Airport. Department of Conservation and RecreationMassachusetts Dept. of Conservation and Recreation sealAgency logoDepartment overviewFormed2003Preceding agenciesMetropolitan District CommissionDepartment of Environmental ManagementJurisdictionMassachusetts, United StatesHeadquarters251 Causeway Street, BostonDepartment executiveDoug Rice, CommissionerWebsite[1] The Depar...