Büyük O gösterimi
|
Read other articles:

Samuel Waldegrave, from The Illustrated London News Samuel Waldegrave's tomb in Carlisle Cathedral Hon. Samuel Waldegrave (13 September 1817 – 1 October 1869) was Bishop of Carlisle from 1860 until his death. The second son of the 8th Earl Waldegrave, he was educated at Cheam School and graduated B.A. from Balliol College, Oxford in 1839.[1] In 1842, he became a deacon and was then curate to St Ebbe's, Oxford and rector of Barford St Martin in 1844. He was then canon of Salisbur...

Sveriges Olympiska Kommitté Олімпійський комітет Швеції Абревіатура SOK(швед.)[1], SOC(англ.)[2]Тип Національний олімпійський комітетЗасновано 1913Олімпійський стадіон (Стокгольм)[1][2]Правовий статус Неприбуткова організаціяМета розвиток спорту та олімпійського руху

Alejandro Arribas Arribas bermain untuk Rayo VallecanoInformasi pribadiNama lengkap Alejandro Arribas GarridoTanggal lahir 1 Mei 1989 (umur 34)Tempat lahir Madrid, SpainTinggi 1,82 m (6 ft 0 in)Posisi bermain Bek tengahInformasi klubKlub saat ini SevillaNomor 24Karier junior Rayo MajadahondaKarier senior*Tahun Tim Tampil (Gol)2007–2008 Rayo Majadahonda 2008–2010 Rayo B 47 (0)2009 → Navalcarnero (pinjam) 15 (1)2010–2012 Rayo Vallecano 74 (2)2012–2014 Osasuna 70 (3...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2018) تدخل منطقة البحر الأبيض المتوسط-داش للتخلف عن التأخر في التغذية العصبية، أو بشكل أكثر شيوعًا، حمية ميند ، يجمع بين أجزاء من النظام الغذائي (النمط الغذائى لوق

Latvian ice dancer (born 1997) Olga JakušinaOther namesJakushina/YakushinaBorn (1997-05-26) 26 May 1997 (age 26)Jelgava, LatviaHeight1.70 m (5 ft 7 in)Figure skating careerCountryLatviaPartnerAndrey NevskiyCoachAlexander ZhulinSkating clubKristal Ice FSCBegan skating2001 Olga Jakušina (born 26 May 1997) is a Latvian ice dancer. With Andrey Nevskiy, she is the 2015 Volvo Open Cup silver medalist and 2014 Tallinn Trophy bronze medalist. They have competed at three World Ch...
Saltos ornamentais nosJogos Olímpicos de Verão de 2012 Trampolim 3 m Individual masc fem Sincronizado masc fem Plataforma 10 m Individual masc fem Sincronizado masc fem A competição de saltos ornamentais na modalidade trampolim 3 metros sincronizado masculino foi disputada no dia 1 de agosto no Centro Aquático, em Londres.[1][2] Medalhistas Ouro CHN Luo Yutong e Qin Kai Prata RUS Ilya Zakharov e Evgeny Kuznetsov Bronze USA Troy Dumais e Kristian Ipsen Resultados Pos. Atletas Saltos Total...

Legislative body of the province of Zamboanga del Norte, Philippines Zamboanga del Norte Provincial Board Sangguniang Panlalawigan ng Zamboanga del NorteTypeTypeUnicameral Term limits3 terms (9 years)LeadershipPresiding OfficerJulius Napigquit, PDP–Laban since June 30, 2022 StructureSeats13 board members1 ex officio presiding officerPolitical groups PDP–Laban (9) Nacionalista (1) Nonpartisan (2) Length of term3 yearsAuthorityLocal Government Code of the Philippine...

Australian professional football player (born 1993) Connor Pain Pain with the Young Socceroos in 2013Personal informationFull name Connor Thomas Pain[1]Date of birth (1993-11-11) 11 November 1993 (age 30)Place of birth Sha Tin, British Hong Kong[2]Height 1.75 m (5 ft 9 in)[3]Position(s) WingerTeam informationCurrent team Al-OrobahNumber 7Senior career*Years Team Apps (Gls)2010–2011 Malvern City 20 (4)2012 Bentleigh Greens 19 (1)2012–2016 Melbour...

Subspecies of fish Kirikuchi char Conservation status Endangered (IUCN 2.3)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Salmoniformes Family: Salmonidae Genus: Salvelinus Species: S. leucomaenis Subspecies: S. l. japonicus Trinomial name Salvelinus leucomaenis japonicusŌshima, 1961 Synonyms[1] Salvelinus japonicus The kirikuchi char, Salvelinus leucomaenis japonicus, is a freshwater fish in the ...

الطباعة الملحية كانت العملية التصويرية الورقية السائدة لإنتاج صور موجبة مطبوعة في الفترة الزمنية الممتدة من عام 1839 وحتى حوالي عام 1860.[1][2] اختُرعت تقنية الطباعة الملحية في منتصف الثلاثينيات من القرن ال19 من قبل العالم والمخترع الإنكليزي وليم فوكس تالبوت. لقد قام بص�...

103rd season in existence of Arsenal F.C. Arsenal 1988–89 football seasonArsenal1988–89 seasonChairmanPeter Hill-WoodManagerGeorge GrahamFirst Division1stFA CupThird roundLeague CupThird roundLeague Centenary TrophyWinnersTop goalscorerLeague: Alan Smith (23)All: Alan Smith (25)Highest home attendance54,029 vs. Liverpool (9 November 1988)Lowest home attendance17,885 vs. Hull City (12 October 1988)Average home league attendance34,477[1] Home colours Away colours ← 1987�...

Indian actress (born 1985) Radhika ApteApte in 2018Born (1985-09-07) 7 September 1985 (age 38)Vellore, Tamil Nadu, IndiaAlma materFergusson CollegeOccupationActressYears active2005–presentSpouse Benedict Taylor (m. 2012) Radhika Apte (born 7 September 1985) is an Indian actress who works primarily in Hindi, Tamil, Telugu and Marathi films. Apte has received several awards including an International Emmy Award nomination, thus becoming the first ...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Kim Kitsuragi – news · newspapers · books · scholar · JSTOR (October 2023) ...

1935 film by Ray Enright For the 1933 animated film, see We're in the Money (1933 film). For song from the film Gold Diggers of 1933, see The Gold Diggers' Song (We're in the Money). We're in the MoneyFilm posterDirected byRay EnrightWritten byF. Hugh HerbertBrown HolmesStory byGeorge BilsonStarringJoan BlondellGlenda FarrellCinematographyArthur L. ToddEdited byOwen MarksMusic byHeinz RoemheldLeo F. ForbsteinDistributed byWarner Bros.Release date August 17, 1935 (1935-08-17) Ru...

Species of gastropod Odontocymbiola americana Apertural view of Odontocymbiola americana Scientific classification Kingdom: Animalia Phylum: Mollusca Class: Gastropoda (unranked): clade Caenogastropodaclade Hypsogastropodaclade Neogastropoda Superfamily: Muricoidea Family: Volutidae Subfamily: Cymbiinae Genus: Odontocymbiola Species: O. americana Binomial name Odontocymbiola americana(Reeve, 1856) Synonyms Odontocymbiola macaensis Calvo & Coltro, 1997 Odontocymbiola saotomensis Calvo...

Photo du groupe Ace of Base durant un concert en 2008 La liste des chansons suivante a été enregistrée par le groupe suédois Ace of Base. Sommaire : Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 0-9 Chanson Artiste(s) Écriture Album(s) Date Réf. Adventures in Paradise Ace of Base Jonas « Joker » Berggren Cruel Summer Flowers 1998 All for You Ace of Base The Golden Ratio 2010 All That She Wants Ace of Base Jonas « Joker » Berggren Ulf « Bud...

Former ice hockey team in the NHL For other uses, see Hamilton Tigers (disambiguation). Hamilton TigersFounded1878HistoryQuebec Bulldogs1878–1920Hamilton Tigers1920–1925Home arenaBarton Street ArenaCityHamilton, OntarioTeam coloursBlack, gold, white The Hamilton Tigers were a professional ice hockey team based in Hamilton, Ontario. They competed in the National Hockey League (NHL) from 1920 to 1925. The Tigers were formed by the sale of the Quebec Bulldogs NHL franchis...

This article is about the 1993 album. For similarly named albums, see Honky Tonk Angel (disambiguation). For the 1952 song, see It Wasn't God Who Made Honky Tonk Angels. 1993 studio album by Dolly Parton, Loretta Lynn and Tammy WynetteHonky Tonk AngelsStudio album by Dolly Parton, Loretta Lynn and Tammy WynetteReleasedNovember 2, 1993RecordedFebruary 1993StudioNightingale Studio (Nashville)Masterfonics (Nashville)The Doghouse (Nashville)GenreCountryLength32:34LabelColumbia NashvillePr...

Cette cathédrale n’est pas la seule cathédrale Saint-Georges. Cathédrale Saint-Georges La cathédrale Saint-Georges Présentation Nom local ቅዱስ ጊዮርጊስ ቤተክርስቲያን Culte Christianisme éthiopien orthodoxe Type Cathédrale Début de la construction 1896 Fin des travaux 1896 Architecte Sebastiano Castagna Autres campagnes de travaux Restaurée après la Libération (1941) Style dominant Octogonal Géographie Pays Éthiopie Ville Addis-Abeba Coordonnées 9° ...



















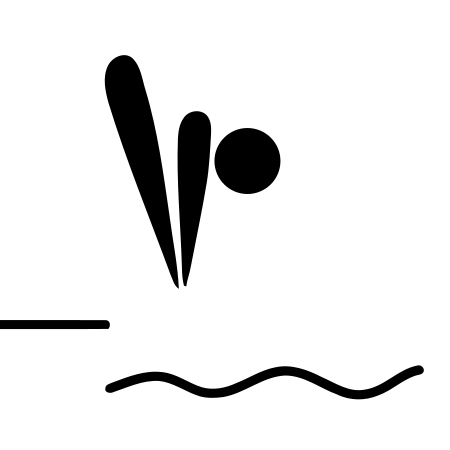
![{\displaystyle O([\log n]^{c})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb079b1fd64da744fc661d4c1c9e9d83a13eb447)




























