Konvex mängd
|
Read other articles:

Ini adalah nama Melayu; nama Onn merupakan patronimik, bukan nama keluarga, dan tokoh ini dipanggil menggunakan nama depannya, Hussein. Yang Amat Berbahagia TunHussein OnnSMNحسين عونPerdana Menteri Malaysia ke-3Digelar sebagaiBapak PersatuanBapa Perpaduanباڤ ڤرڤادوانMasa jabatan15 Januari 1976 – 16 Juli 1981Penguasa monarkiYahya PetraAhmad ShahWakilMahathir MohamadPendahuluAbdul Razak HusseinPenggantiMahathir MohamadWakil Perdana Menteri Malaysia ke-3Masa jaba...

Artikel ini bukan mengenai Sindo, acara berita Sindo TV. Seputar IndonesiaLogo terakhir Seputar IndonesiaGenreProgram beritaPengembangRCTIPresenterTommy TjokroNawayogi KusumaRizky HasanRyanka PutraTasya SyariefLedi MarinaNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim28RilisJaringan asliRCTI (1989-2017)SCTV (1990-1996)Rilis asli25 Agustus 1989 –31 Oktober 2017Pranala luarSitus web Seputar Indonesia (juga disingkat sebagai Sindo) adalah program berita pertama yang diproduksi ...

Almazán municipio de EspañaBanderaEscudo Plaza de la localidad AlmazánUbicación de Almazán en España. AlmazánUbicación de Almazán en la provincia de Soria. Mapa interactivo — AlmazánPaís España• Com. autónoma Castilla y León• Provincia Soria• Comarca Comarca de Almazán• Partido judicial AlmazánUbicación 41°29′09″N 2°31′59″O / 41.485833333333, -2.5330555555556• Altitu...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) بريم جوشوا معلومات شخصية الميلاد سنة 1946 (العمر 76–77 سنة)[1] مواطنة ألمانيا الحياة العملية المهنة موسيقي اللغات الألمانية المواقع IMDB صف�...

Cet article est une ébauche concernant l’astronomie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Un interféromètre astronomique est un réseau de télescopes ou segments de miroirs qui agissent ensemble aux fins de détection avec une résolution plus grande, via l'interférométrie. L'avantage d'un interféromètre est que son pouvoir de résolution est le même que celui d'un télescope avec la même o...

Nota: Para outros significados, veja DOP. Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Junho de 2019) Versão portuguesa do logotipo que acompanha os produtos com Denominação de Origem Protegida (DOP) pela União Europeia. Sidra Natural Piñera, DOP Queijo Stilton Azul, DOP A...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2021) يندرج مصطلح إعادة التأهيل البصري (أو إعادة تأهيل الرؤية) تحت تصنيف إعادة التأهيل الطبي، ويهدف لتحسين الرؤية أو ضعف البصر. أو بمعنى آخر هي عملية استعادة القدرة

Este artigo não cita fontes confiáveis. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Fevereiro de 2019) Coordenadas: 40° 25' 24 N, 3° 41' 23 W Biblioteca Nacional de España Biblioteca Nacional da Espanha Fachada da Biblioteca Nacional da Espanha em Madrid. País Espanha Tipo Pública Estabelecida 29 de dezembro de 1711 (311 anos) Lo...

American sports pay television network For the Canadian version of this channel, see NBA TV Canada. For the Philippine version of this channel, see NBA TV Philippines. Television channel NBA TVCountryUnited StatesBroadcast areaWorldwideHeadquartersAtlanta, Georgia, U.S.ProgrammingLanguage(s)EnglishPicture format1080i HDTV(downscaled to letterboxed 480i for the SDTV feed)OwnershipOwnerNational Basketball Association(operated by TNT Sports)Sister channelsMLB NetworkMotor TrendAT&T SportsNet...

This article is about the series of animated short films. For other uses, see Fireball (disambiguation). FireballCover of the first DVD volumeファイアボール(Faiabōru)GenreScience fiction Anime television seriesDirected byWataru ArakawaWritten byWataru ArakawaMusic byYoshiyuki UsuiStudio Jinni's Animation Studios Walt Disney Television International Japan Original run April 7, 2008 – June 30, 2008Episodes13 (List of episodes) Anime television seriesFireball CharmingDir...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Masjid Raya Al-Falah Sragen adalah sebuah Masjid yang terletak di Sragen,Kabupaten Sragen,Jawa Tengah. Masjid Raya Al-Falah SragenAgamaAfiliasi agamaIslamLokasiLokasiSragen,Kabupaten Sragen,Jawa Tengah.Koordinat{{WikidataCoord}} – missing coordinate ...

This literature-related list is incomplete; you can help by adding missing items. (June 2022) Alternative list formats Alphabetical Chronological vte This is a chronological list of women playwrights who were active in England and Wales, and the Kingdom of Great Britain and Ireland before approximately 1800, with a brief indication of productivity. (For a chronological list, see the link on the right.) Nota Bene: Authors of dramatic works are the focus of this list, though many of these write...

For other uses, see Still Bill (disambiguation). 1972 studio album by Bill WithersStill BillStudio album by Bill WithersReleasedMay 1972StudioThe Record Plant (Los Angeles)GenreSoulR&BfunkbluesLength36:14LabelSussexProducerBenorce BlackmonWithersJames GadsonMelvin DunlapRay JacksonBill Withers chronology Just as I Am(1971) Still Bill(1972) Live at Carnegie Hall(1973) Singles from Still Bill Lean on MeReleased: April 21, 1972 Use MeReleased: 1972 Kissing My LoveReleased: 1973 Still...

M.A.B. PaintsTypePublicIndustryPaint/CoatingsFounded1899HeadquartersBroomall, PA, U.S.ProductsPaintIndustrial coatingPainting equipmentRevenue$146,000,000OwnerSherwin-WilliamsNumber of employees730 (2006)Websitewww.mabpaints.com M.A.B. Paints (officially M.A. Bruder & Sons Inc.) was a regional manufacturer of architectural, commercial and industrial coatings for the professional and do-it-yourself markets. Founded in 1899 in South Philadelphia by Michael A. Bruder, M.A.B. Paints grew to o...

This article is about the 1979 Mi-Sex song. For the 1978 Yellow Magic Orchestra song, see Yellow Magic Orchestra (album). 1979 single by Mi-SexComputer GamesSingle by Mi-Sexfrom the album Graffiti Crimes ReleasedSeptember 1979 (Australia/NZ)Recorded1979GenreSynth-popLength3:54LabelCBSSongwriter(s) Murray Burns Steve Gilpin Kevin Stanton Producer(s)Peter DawkinsMi-Sex singles chronology But You Don't Care (1979) Computer Games (1979) People (1980) Computer Games is a song by New Zealand band M...

Fijian rugby union player (born 1984) Rugby playerVereniki GonevaGoneva in 2014Birth nameVereniki GonevaDate of birth (1984-04-05) 5 April 1984 (age 39)Place of birthLautoka, FijiHeight5.9 ft (1.79 m)Weight102 kg (16 st 1 lb; 225 lb)SpouseRaijeli KatalauRugby union careerPosition(s) Wing, Centre, FullbackCurrent team Mont-de-MarsanSenior careerYears Team Apps (Points)2009–2011 US Colomiers 46 (28)2011–2012 Tarbes 19 (40)2012–2016 Leicester Tigers 89 (2...

Traditional blues song Bottle It Up and GoSingle by Tommy McClennanA-sideWhiskey Headed WomanReleased1939 (1939)RecordedNovember 22, 1939StudioRCA Studio A, ChicagoGenreBluesLength2:46LabelBluebirdSongwriter(s)Unknown Bottle Up and Go or Bottle It Up and Go is a song that is a standard of the blues.[1] Based on earlier songs, Delta bluesman Tommy McClennan recorded Bottle It Up and Go in 1939. The song has been interpreted and recorded by numerous artists, sometimes using alterna...

Sân bay quốc tế Simón BolívarAeropuerto de Maiquetia Mã IATACCS Mã ICAOSVMI Thông tin chungKiểu sân bayPublicChủ sở hữuIAAMCơ quan quản lýInstituto Autónomo del Aeropuerto Internacional de MaiquetíaThành phốCaracasVị tríCaracasĐộ cao235 ft / 72 mTọa độ10°36′11″B 066°59′26″T / 10,60306°B 66,99056°T / 10.60306; -66.99056Trang mạngwww.aeropuerto-maiquetia.com.veĐường băng Hướng Chiều dài Bề mặt ...

Annual British football reference book The Football YearbookOriginal titleRothmans Football YearbookLanguageEnglishGenreAlmanacPublisherHeadlineNo. of books52 The Football Yearbook (formerly Rothmans Football Yearbook and Sky Sports Football Yearbook) is a British football reference book published annually by Headline (a division of Hodder Headline). It was first published in 1970 for the 1970–71 season, its first compilers being Tony Williams and Roy Peskett.[1] For many years the ...

Municipio de Clearwater Municipio Municipio de ClearwaterUbicación en el condado de Wright en Minnesota Ubicación de Minnesota en EE. UU.Coordenadas 45°22′09″N 94°01′46″O / 45.369166666667, -94.029444444444Entidad Municipio • País Estados Unidos • Estado Minnesota • Condado WrightSuperficie • Total 60.71 km² • Tierra 56.95 km² • Agua (6.19 %) 3.76 km²Altitud • Media 314 m s. n....

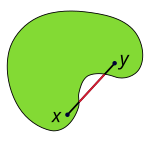

![{\displaystyle \lambda x_{1}+(1-\lambda )x_{2}\in X\quad \forall \quad \lambda \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f2db4b6f93f325075721ae62912ba6d11ac22d2)






![{\displaystyle \lambda x_{1}+(1-\lambda )x_{2},\ \lambda \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22314a9a215989ac3bc7b931548a067e936c7346)













![{\displaystyle x=(1-\lambda )x^{(1)}+\lambda x^{(2)},{\mbox{ med }}\lambda \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcce670c74988b1ff5a28d7f119b1ab7462ca9f9)



![{\displaystyle \sum _{j=1}^{n}a_{ij}[(1-\lambda )x_{j}^{(1)}+\lambda x_{j}^{(2)}]\leq b_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60abf450415866a0651f35a457300a85f8664da5)

