Привидна звездана величина
|
Read other articles:

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2019) تاكاشي موراكامي معلومات شخصية الميلاد 25 مايو 1944 (79 سنة) شيزوكا مواطنة اليابان الحياة العملية المهنة لاعب غولف الرياضة غولف تعديل مصدري - تعدي...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Menara air Manggarai Menara air Manggarai adalah bangunan di Manggarai, Jakarta Selatan yang dibuat sekitar tahun 1918. Menara ini digunakan untuk menyalurkan air di daerah Jakarta dengan menggunakan teknologi bejana berhubungan dari sumber air di Bog...

Apodemia virgulti Classificação científica Domínio: Eukaryota Reino: Animalia Filo: Arthropoda Classe: Insecta Ordem: Lepidoptera Família: Riodinidae Tribo: Emesidini Gênero: Apodemia Espécies: A. virgulti Nome binomial Apodemia virgulti(Behr, 1865) Apodemia virgulti é uma espécie de borboleta na família de borboletas conhecida como Riodinidae.[1][2] Pode ser encontrada na América do Norte.[1] O número MONA ou Hodges de Apodemia virgulti é 4402.1.[3] Subespéc...

Track map. The 2002 Cadillac Grand Prix of Washington, D.C. was the fifth round of the 2002 American Le Mans Series season. It took place in a 1.66 mi (2.67 km) temporary street circuit set around the streets and parking lot adjacent to Robert F. Kennedy Memorial Stadium in Washington, D.C., on July 21, 2002. The venue was not renewed for another season due to complaints from neighbors about noise and the race was the only event of its kind held in Washington.[1] The event w...

بندر أمجز بندرامجز - قرية - تقسيم إداري البلد إيران المحافظة كرمان المقاطعة عنبر أباد الناحية الناحية المركزية (مقاطعة عنبر أباد) القسم الريفي قسم أمجز الريفي (مقاطعة عنبر أباد) السكان معلومات أخرى التوقيت توقيت إيران (+3:30 غرينيتش) توقيت صيفي توقيت إيران (+4:30) �...

Arnett Cobb (rechts) met bandleider Lionel Hampton (in de lucht), in New York. circa juni 1946 (foto:William Gottlieb) Arnette Cleophus Cobb (Houston, 10 augustus 1918 – aldaar, 24 maart 1989) was een Amerikaanse jazz-tenorsaxofonist. Hij was een energieke tough saxofoonspeler in de swing-traditie. Biografie Cobb begon zijn muzikale carrière in de lokale bands van Chester Boone (1934-1936) en Milt Larkin (1936-1942). Bij Larkin speelde hij naast onder meer Illinois Jacquet, Eddie Cleanhead...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) الدوري الإسباني الدرجة الثانية 1934–35 تفاصيل الموسم دوري الدرجة الثانية الإسباني البلد إسبانيا ال�...

2008 video gameElebits: The Adventures of Kai and ZeroDeveloper(s)KonamiPublisher(s)KonamiDesigner(s)Shingo Mukaitoge (producer)[1]Composer(s)Maki KiriokaHiroshi TanabePlatform(s)Nintendo DSReleaseJP: December 11, 2008NA: January 6, 2009EU: February 20, 2009Genre(s)ActionMode(s)Single-player, multiplayer Elebits: The Adventures of Kai and Zero (エレビッツ カイとゼロの不思議な旅, Elebits: Kai to Zero no Fushigi na Tabi), known as Eledees: The Adventures of Kai and Zero ...

Line of consumer-oriented laptop computers and tablets Lenovo YogaDeveloperLenovoManufacturerWistronType2-in-1 PCLifespan2012; 11 years ago (2012)Operating systemWindows/LinuxCPUAMD APU, AMD RyzenIntel Core i3/i5/i7Display11.6-15, with touchscreenGraphicsAMD Radeon (Pro), Nvidia GeForce/QuadroInputKeyboard, touchpad (trackpoint only for Thinkpad sub-line)CameraCamera with integrated microphone (front-facing)Marketing targetConsumer / Home purposeRelatedThinkPad Yoga sub-line...

American football player (1909–2004) Not to be confused with Dixie Roberts. Dixie RobertsVanderbilt Commodores – No. 4PositionHalfbackMajorEngineeringPersonal informationBorn:(1909-07-20)July 20, 1909Cassville, White County, TennesseeDied:August 17, 2004(2004-08-17) (aged 95)Nashville, TennesseeWeight174 lb (79 kg)Career historyCollegeVanderbilt (1930–1932)High schoolMcMinnville CentralCareer highlights and awards All-Southern (1932) William Clyde Dixie R...

Metro station in Shenzhen, Guangdong, China Yangtai Mountain East阳台山东PlatformGeneral informationLocationLonghua District, Shenzhen, GuangdongChinaCoordinates22°40′15″N 113°59′12″E / 22.670765°N 113.986582°E / 22.670765; 113.986582Operated bySZMC (Shenzhen Metro Group)Line(s) Line 6Platforms2 (1 island platform)Tracks2ConstructionStructure typeElevatedAccessibleYesHistoryOpened18 August 2020Services Preceding station Shen...
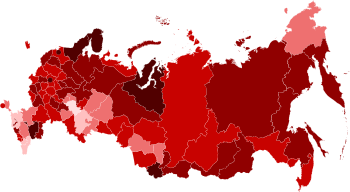
Artikel ini mendokumentasikan suatu disease pandemic terkini. Informasi mengenai hal itu dapat berubah dengan cepat jika informasi lebih lanjut tersedia; laporan berita dan sumber-sumber primer lainnya mungkin tidak bisa diandalkan. Pembaruan terakhir untuk artikel ini mungkin tidak mencerminkan informasi terkini mengenai disease pandemic ini untuk semua bidang. Artikel ini bukan mengenai Pandemi Covid-19 di Polandia atau Pandemi Covid-19 di Spanyol. Pandemi Koronavirus di RusiaKasus yang ter...

2000 American film$pentDirected byGil Cates Jr.Written byGil Cates Jr.Produced byJordan SummersRana Joy GlickmanGil Cates Jr.StarringJason LondonCharlie SpradlingErin BeauxPhill LewisCinematographyRobert D. TomerEdited byJonathan CatesMusic byStan RidgwayDistributed byRegent EntertainmentRelease date July 21, 2000 (2000-07-21) (US) Running time91 minutesCountryUnited StatesLanguageEnglishBox office$9,287 $pent is a 2000 drama film directed by Gil Cates Jr. and starring Jaso...

Rijeka Open 2007 Sport Tennis Data 7 maggio - 13 maggio Campioni Singolare Marin Čilić Doppio Jérôme Haehnel / Jean-René Lisnard 2008 Il Rijeka Open 2007 è stato un torneo di tennis facente parte della categoria ATP Challenger Series nell'ambito dell'ATP Challenger Series 2007. Il torneo si è giocato a Fiume (Rijeka) in Croazia dal 7 al 13 maggio 2007 su campi in terra rossa e aveva un montepremi di $30 000+H. Indice 1 Vincitori 1.1 Singolare 1.2 Doppio 2 Collegamenti esterni Vincitori...

American hammer thrower Loree SmithPersonal informationNationalityAmericanBorn (1982-11-06) November 6, 1982 (age 41)Melbourne, Florida, U.S.Height5 ft 6 in (1.68 m)[1]SportTurned pro2008Updated on August 24, 2008. Loree Smith (born November 6, 1982) is an American hammer thrower. Early years Smith said she played sports just to pass the time growing up. When asked to describe her start in track and field, she said she was just a chubby kid throwing 25 feet in the ...

Wakil Wali Kota ProbolinggoLambang Kota Probolinggo Republik IndonesiaPetahanamasih lowongsejak 9 Desember 2020Masa jabatan5 tahunDibentuk2004Pejabat pertamaBandyk SutrisnoSitus webprobolinggokota.go.id Wakil Wali Kota Probolinggo adalah posisi kedua yang memerintah Kota Probolinggo di bawah Wali Kota Probolinggo. Posisi ini pertama kali dibentuk pada tahun 2004. Daftar No Wakil Wali Kota Mulai Jabatan Akhir Jabatan Prd. Ket. Wali Kota 1 Bandyk Sutrisno 2004 2009 1 H.M. BuchoriS.H...

On Virtues and Vices (Greek: Περὶ Ἀρετῶν καὶ Κακιῶν; Latin: De Virtutibus et Vitiis Libellus) is the shortest of the four ethical treatises attributed to Aristotle. The work is now regarded as spurious by scholars and its true origins are uncertain though it was probably created by a member of the peripatetic school.[1] See also Eudemian Ethics Magna Moralia Nicomachean Ethics Notes ^ Zeller (1883:145). References Zeller, Eduard (1883). A History of Eclecticism...

Unorganized BoroughboroughUnorganized Borough – VedutaLa stazione di Nenana. LocalizzazioneStato Stati Uniti Stato federato Alaska TerritorioCoordinate57°30′N 156°42′W / 57.5°N 156.7°W57.5; -156.7 (Unorganized Borough)Coordinate: 57°30′N 156°42′W / 57.5°N 156.7°W57.5; -156.7 (Unorganized Borough) Superficie969 318 km² Abitanti77 393 (2009) Densità0,08 ab./km² Altre informazioniFuso orarioUTC-9 CartografiaUnorgan...

Dirty MoneyTitolo originaleDirty Money PaeseStati Uniti d'America Anno2018 Generedocumentario Edizioni2 Puntate12 Durata50-77 minuti (a episodio) Lingua originaleinglese RealizzazioneProduttore esecutivoAdam Del Deo, Yon Motskin, Lisa Nishimura, Stacey Offman, Jason Spingarn-Koff, Alex Gibney Casa di produzioneJigsaw Productions DistributoreNetflix Manuale Dirty Money è una serie documentaristica statunitense che racconta storie di corruzione aziendale e di reati finanziari.[1] Tutti...

حملة بلاد الرافدين جزء من الحرب العالمية الأولى الخنادق العثمانية خلال حصار الكوت معلومات عامة التاريخ 6 نوفمبر 1914 إلى 14 نوفمبر 1918 الموقع بلاد الرافدين (العراق الآن) النتيجة انتصار الحلفاء، معاهدة سيفر الانتداب البريطاني على العراق المتحاربون المملكة المتحدة الهند البري...
![{\displaystyle {\sqrt[{5}]{100}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d26eff2c044a521107db3cf827e04c2b8415691d)





