Центрированные многоугольные числа

Не следует путать с центральными многоугольными числами — количеством частей на которые можно разрезать круг данным количество разрезов.

Центрированные многоугольные числа — класс плоских ${\displaystyle k}$-угольных фигурных чисел (${\displaystyle k\geqslant 3}$), получаемый следующим геометрическим построением. Сначала на плоскости фиксируется некоторая центральная точка. Затем вокруг неё строится правильный ${\displaystyle k}$-угольник с ${\displaystyle k}$ точками вершин, каждая сторона содержит две точки (см. рисунок). Далее снаружи строятся новые слои ${\displaystyle k}$-угольников, причём каждая их сторона на новом слое содержит на одну точку больше, чем в предыдущем слое, то есть начиная со второго слоя каждый следующий слой содержит на ${\displaystyle k}$ больше точек, чем предыдущий. Общее число точек внутри каждого слоя и принимается в качестве центрированного многоугольного числа (точка в центре считается начальным слоем)^[1].

Примеры построения центрированных многоугольных чисел:

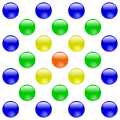
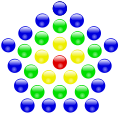
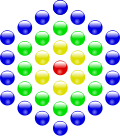
Треугольные	Квадратные	Пятиугольные	Шестиугольные

Из построения видно, что центрированные многоугольные числа получаются как частичные суммы следующего ряда: ${\displaystyle 1+k+2k+3k+4k+\dots }$ (например, центрированные квадратные числа, для которых ${\displaystyle k=4,}$ образуют последовательность: ${\displaystyle 1,5,13,25,41\dots }$) Этот ряд можно записать как ${\displaystyle 1+k(1+2+3+4+\dots ).}$, откуда видно, что в скобках — порождающий ряд для классических треугольных чисел. Следовательно, каждая последовательность центрированных ${\displaystyle k}$-угольных чисел, начиная со 2-го элемента, может быть представлена как ${\displaystyle kT_{n}+1,}$ где ${\displaystyle T_{n}(n=1,2,3\dots )}$ — последовательность треугольных чисел. Например, центрированные квадратные числа — это учетверённые треугольные числа плюс 1, порождающий ряд для них имеет вид: ${\displaystyle 1+4+8+12\dots }$^[2]

Общая формула^[2] для ${\displaystyle n}$-го центрированного ${\displaystyle k}$-угольного числа ${\displaystyle C_{n}^{(k)}}$:

${\displaystyle C_{n}^{(k)}=1+k{\frac {n(n-1)}{2}}={\frac {kn^{2}-kn+2}{2}};\ n=1,2,3\dots }$

(ОЦФ)

Сводная таблица

Число углов k	Тип числа	Начало последовательности	Ссылка на OEIS
3	Центрированные треугольные числа	1, 4, 10, 19, 31, …	A005448
4	Центрированные квадратные числа	1, 5, 13, 25, 41, …	A001844
5	Центрированные пятиугольные числа	1, 6, 16, 31, 51, …	A005891
6	Центрированные шестиугольные числа	1, 7, 19, 37, 61, …	A003215
7	Центрированные семиугольные числа	1, 8, 22, 43, 71, …	A069099
8	Центрированные восьмиугольные числа	1, 9, 25, 49, 81, …	A016754
9	Центрированные девятиугольные числа	1, 10, 28, 55, 91, …	A060544
10	Центрированные десятиугольные числа	1, 11, 31, 61, 101, …	A062786

и так далее.

Примечания

1. Деза Е., Деза М., 2016, с. 39—40.
2. Деза Е., Деза М., 2016, с. 40—41.

Литература

• Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 30. — 320 с. — ISBN 5-09-006575-6.
• Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
• Деза Е., Деза М. Фигурные числа. — М.: МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.

Ссылки

• Weisstein, Eric W. Centered polygonal number (англ.) на сайте Wolfram MathWorld.
• Фигурные числа