–Ъ–≤–∞–љ—В–Њ–≤–Њ–µ —А–∞–Ј–і–µ–ї–µ–љ–Є–µ —Б–µ–Ї—А–µ—В–∞ вАФ –Ї–≤–∞–љ—В–Њ–≤–∞—П –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є—З–µ—Б–Ї–∞—П —Б—Е–µ–Љ–∞ –і–ї—П –±–µ–Ј–Њ–њ–∞—Б–љ–Њ–є —Б–≤—П–Ј–Є, –Ї–Њ—В–Њ—А–∞—П –≤—Л—Е–Њ–і–Є—В –Ј–∞ —А–∞–Љ–Ї–Є –њ—А–Њ—Б—В–Њ–≥–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –Ї–ї—О—З–µ–є . –Ю–љ–∞ –Љ–Њ–і–Є—Д–Є—Ж–Є—А—Г–µ—В –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї—Г—О —Б—Е–µ–Љ—Г —А–∞–Ј–і–µ–ї–µ–љ–Є—П —Б–µ–Ї—А–µ—В–∞ , –Є—Б–њ–Њ–ї—М–Ј—Г—П –Ї–≤–∞–љ—В–Њ–≤—Г—О –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—О –Є —В–µ–Њ—А–µ–Љ—Г –Њ –Ј–∞–њ—А–µ—В–µ –Ї–ї–Њ–љ–Є—А–Њ–≤–∞–љ–Є—П –і–ї—П –і–Њ—Б—В–Є–ґ–µ–љ–Є—П —Г–≤–µ–ї–Є—З–µ–љ–љ–Њ–є –±–µ–Ј–Њ–њ–∞—Б–љ–Њ—Б—В–Є –Ї–Њ–Љ–Љ—Г–љ–Є–Ї–∞—Ж–Є–є.
–Ь–µ—В–Њ–і —А–∞–Ј–і–µ–ї–µ–љ–Є—П —Б–µ–Ї—А–µ—В–∞ —Б–Њ—Б—В–Њ–Є—В –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ: –Њ—В–њ—А–∞–≤–Є—В–µ–ї—М –ґ–µ–ї–∞–µ—В –њ–Њ–і–µ–ї–Є—В—М—Б—П —Б–µ–Ї—А–µ—В–Њ–Љ —Б —А—П–і–Њ–Љ —Б—В–Њ—А–Њ–љ-–њ–Њ–ї—Г—З–∞—В–µ–ї–µ–є —В–∞–Ї–Є–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ, —З—В–Њ–±—Л —Б–µ–Ї—А–µ—В –±—Л–ї –њ–Њ–ї–љ–Њ—Б—В—М—О —А–∞—Б–Ї—А—Л—В —В–Њ–ї—М–Ї–Њ –≤ —В–Њ–Љ —Б–ї—Г—З–∞–µ, –µ—Б–ї–Є –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –±–Њ–ї—М—И–∞—П —З–∞—Б—В—М –њ–Њ–ї—Г—З–∞—В–µ–ї–µ–є —А–∞–±–Њ—В–∞–µ—В –≤–Љ–µ—Б—В–µ. –Ю–і–љ–∞–Ї–Њ, –µ—Б–ї–Є –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ –њ–Њ–ї—Г—З–∞—В–µ–ї–µ–є, —А–∞–±–Њ—В–∞—О—Й–Є—Е –≤–Љ–µ—Б—В–µ, –љ–µ —Е–≤–∞—В–∞–µ—В, —З—В–Њ–±—Л —А–∞—Б–Ї—А—Л—В—М —Б–µ–Ї—А–µ—В, —Б–µ–Ї—А–µ—В –Њ—Б—В–∞—С—В—Б—П —Б–Њ–≤–µ—А—И–µ–љ–љ–Њ –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л–Љ.
–Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–∞—П —Б—Е–µ–Љ–∞ –±—Л–ї–∞ –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ –њ—А–µ–і–ї–Њ–ґ–µ–љ–∞ –Р–і–Є –®–∞–Љ–Є—А–Њ–Љ [ 1] –Ф–ґ–Њ—А–і–ґ–µ–Љ –С–ї—Н–Ї–ї–Є [ 2] –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Б–Њ—Б—В–Њ—П–љ–Є—П –і–ї—П —Б–Њ–Ј–і–∞–љ–Є—П –±–µ–Ј–Њ–њ–∞—Б–љ–Њ–≥–Њ –Ї–ї—О—З–∞ , –Ї–Њ—В–Њ—А—Л–є –Љ–Њ–ґ–µ—В –±—Л—В—М –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ –і–ї—П –њ–µ—А–µ–і–∞—З–Є —Б–µ–Ї—А–µ—В–∞ —Б –њ–Њ–Љ–Њ—Й—М—О –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є—Е –і–∞–љ–љ—Л—Е[ 3] [ 4] [ 5]
–Ъ–≤–∞–љ—В–Њ–≤–Њ–µ —А–∞–Ј–і–µ–ї–µ–љ–Є–µ —Б–µ–Ї—А–µ—В–∞ –њ—А–µ–і–ї–∞–≥–∞–µ—В—Б—П –і–ї—П –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П –≤ –Ї–≤–∞–љ—В–Њ–≤—Л—Е –і–µ–љ—М–≥–∞—Е [ 6] –Ї–≤–∞–љ—В–Њ–≤—Л—Е —Б–µ—В–µ–є –Є —А–∞—Б–њ—А–µ–і–µ–ї—С–љ–љ—Л—Е –Ї–≤–∞–љ—В–Њ–≤—Л—Е –≤—Л—З–Є—Б–ї–µ–љ–Є–є .
–≠—В–Њ—В –њ—А–Є–Љ–µ—А —Б–ї–µ–і—Г–µ—В –Њ—А–Є–≥–Є–љ–∞–ї—М–љ–Њ–є —Б—Е–µ–Љ–µ, —А–∞–Ј—А–∞–±–Њ—В–∞–љ–љ–Њ–є –≤ 1998 –≥–Њ–і—Г. –°—Е–µ–Љ–∞ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В GHZ-—Б–Њ—Б—В–Њ—П–љ–Є–µ –∞–љ–≥–ї. GreenbergerвАУHorneвАУZeilinger state [ 7]
–Я—Г—Б—В—М –Њ—В–њ—А–∞–≤–Є—В–µ–ї—М –Њ–±–Њ–Ј–љ–∞—З–∞–µ—В—Б—П –Ї–∞–Ї –Р–ї–Є—Б–∞ , –∞ –і–≤–∞ –њ–Њ–ї—Г—З–∞—В–µ–ї—П –Ї–∞–Ї –С–Њ–± –Є –І–∞—А–ї–Є. –¶–µ–ї—М –Р–ї–Є—Б—Л вАФ –Њ—В–њ—А–∞–≤–Є—В—М –Ї–∞–ґ–і–Њ–Љ—Г –њ–Њ–ї—Г—З–∞—В–µ–ї—О ¬Ђ—З–∞—Б—В—М¬ї —Б–≤–Њ–µ–≥–Њ —Б–µ–Ї—А–µ—В–љ–Њ–≥–Њ –Ї–ї—О—З–∞ (–љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ —В–Њ–ї—М–Ї–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ) —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —З—В–Њ–±—Л:
–Э–Є –С–Њ–±, –љ–Є –І–∞—А–ї–Є –љ–µ –Є–Љ–µ—О—В –љ–Є–Ї–∞–Ї–Њ–є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є –Њ –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ–Љ –Ї–ї—О—З–µ –Р–ї–Є—Б—Л, –Є –њ–Њ—Н—В–Њ–Љ—Г –љ–Є–Ї—В–Њ –љ–µ –Љ–Њ–ґ–µ—В –Є–Ј–≤–ї–µ—З—М —Б–µ–Ї—А–µ—В —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ.
–¶–µ–ї–Є–Ї–Њ–Љ —Б–µ–Ї—А–µ—В –Љ–Њ–ґ–љ–Њ —Г–Ј–љ–∞—В—М, —В–Њ–ї—М–Ї–Њ –µ—Б–ї–Є –С–Њ–± –Є –І–∞—А–ї–Є –±—Г–і—Г—В —А–∞–±–Њ—В–∞—В—М –≤–Љ–µ—Б—В–µ.
–Я—А–Є—Б—Г—В—Б—В–≤–Є–µ –ї–Є–±–Њ –≤–љ–µ—И–љ–µ–≥–Њ –њ–Њ–і—Б–ї—Г—И–Є–≤–∞—О—Й–µ–≥–Њ, –ї–Є–±–Њ –љ–µ—З–µ—Б—В–љ–Њ–≥–Њ –њ—А–Є—С–Љ–љ–Є–Ї–∞ (–ї–Є–±–Њ –С–Њ–±–∞, –ї–Є–±–Њ –І–∞—А–ї–Є) –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–±–љ–∞—А—Г–ґ–µ–љ–Њ –±–µ–Ј —А–∞—Б–Ї—А—Л—В–Є—П —Б–µ–Ї—А–µ—В–∞. –Р–ї–Є—Б–∞ –Є–љ–Є—Ж–Є–Є—А—Г–µ—В –њ—А–Њ—В–Њ–Ї–Њ–ї, –њ–µ—А–µ–і–∞–≤ –С–Њ–±—Г –Є –І–∞—А–ї–Є –њ–Њ –Њ–і–љ–Њ–є —З–∞—Б—В–Є—Ж–µ –Є–Ј —В—А–Њ–є–Ї–Є GHZ –≤ (—Б—В–∞–љ–і–∞—А—В–љ–Њ–Љ) Z-–±–∞–Ј–Є—Б–µ, —Г–і–µ—А–ґ–Є–≤–∞—П —В—А–µ—В—М—О —З–∞—Б—В–Є—Ж—Г —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ:
|
Ψ ќ® -->
⟩ вЯ© -->
G
H
Z
=
|
000
⟩ вЯ© -->
+
|
111
⟩ вЯ© -->
2
{\displaystyle |\mathrm {\Psi } \rangle _{\rm {GHZ}}={\frac {|000\rangle +|111\rangle }{\sqrt {2}}}}
–≥–і–µ
|
0
⟩ вЯ© -->
{\displaystyle |\mathrm {0} \rangle }
|
1
⟩ вЯ© -->
{\displaystyle |\mathrm {1} \rangle }
–Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ—Л–Љ–Є —Б–Њ—Б—В–Њ—П–љ–Є—П–Љ–Є –≤ –≥–Є–ї—М–±–µ—А—В–Њ–≤–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ .
–Я–Њ—Б–ї–µ —В–Њ–≥–Њ, –Ї–∞–Ї –Ї–∞–ґ–і—Л–є —Г—З–∞—Б—В–љ–Є–Ї –Є–Ј–Љ–µ—А—П–µ—В —Б–≤–Њ—О —З–∞—Б—В–Є—Ж—Г –≤ –•- –Є–ї–Є Y-–±–∞–Ј–Є—Б–µ (–≤—Л–±–Є—А–∞–µ—В—Б—П —Б–ї—Г—З–∞–є–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ), –Њ–љ–Є —Б–Њ–Њ–±—Й–∞—О—В (–њ–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ—Г, –Њ–±—Й–µ—Б—В–≤–µ–љ–љ–Њ–Љ—Г –Ї–∞–љ–∞–ї—Г), –Ї–∞–Ї–Њ–є –±–∞–Ј–Є—Б –Њ–љ–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є –і–ї—П –Є–Ј–Љ–µ—А–µ–љ–Є—П, –љ–Њ –љ–µ —Б–∞–Љ —А–µ–Ј—Г–ї—М—В–∞—В. –Ю–±—К–µ–і–Є–љ–Є–≤ —А–µ–Ј—Г–ї—М—В–∞—В—Л –Є–Ј–Љ–µ—А–µ–љ–Є–є, –С–Њ–± –Є –І–∞—А–ї–Є –Љ–Њ–≥—Г—В –≤—Л—З–Є—Б–ї–Є—В—М, —З—В–Њ –Р–ї–Є—Б–∞ –Љ–Њ–ґ–µ—В –њ–Њ–ї—Г—З–Є—В—М (—Б –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О 1/2) –њ—А–Є –Є–Ј–Љ–µ—А–µ–љ–Є–Є —Б–≤–Њ–µ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П. –Я–Њ–≤—В–Њ—А—П—П —Н—В–Њ—В –њ—А–Њ—Ж–µ—Б—Б –Љ–љ–Њ–≥–Њ —А–∞–Ј, —В—А–Є —Г—З–∞—Б—В–љ–Є–Ї–∞ –Љ–Њ–≥—Г—В —Г—Б—В–∞–љ–Њ–≤–Є—В—М —Б–Њ–≤–Љ–µ—Б—В–љ—Л–є –Ї–ї—О—З –і–ї—П –±–µ–Ј–Њ–њ–∞—Б–љ–Њ–≥–Њ –Њ–±—Й–µ–љ–Є—П.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –љ–∞–≥–ї—П–і–љ—Л–є –њ—А–Є–Љ–µ—А —В–Њ–≥–Њ, –Ї–∞–Ї —Н—В–Њ –±—Г–і–µ—В —А–∞–±–Њ—В–∞—В—М. –Ю–њ—А–µ–і–µ–ї–Є–Љ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ —Б–Њ—Б—В–Њ—П–љ–Є—П —Е –Є —Г —Б–ї–µ–і—Г—О—Й–Є–Љ —Б—В–∞–љ–і–∞—А—В–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ:
|
+
x
⟩ вЯ© -->
=
|
0
⟩ вЯ© -->
+
|
1
⟩ вЯ© -->
2
,
|
− вИТ -->
x
⟩ вЯ© -->
=
|
0
⟩ вЯ© -->
− вИТ -->
|
1
⟩ вЯ© -->
2
{\displaystyle |\mathrm {+x} \rangle ={\frac {|0\rangle +|1\rangle }{\sqrt {2}}},|\mathrm {-x} \rangle ={\frac {|0\rangle -|1\rangle }{\sqrt {2}}}}
|
+
y
⟩ вЯ© -->
=
|
0
⟩ вЯ© -->
+
i
|
1
⟩ вЯ© -->
2
,
|
− вИТ -->
y
⟩ вЯ© -->
=
|
0
⟩ вЯ© -->
− вИТ -->
i
|
1
⟩ вЯ© -->
2
{\displaystyle |\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}}
–Ґ–Њ–≥–і–∞ —Б–Њ—Б—В–Њ—П–љ–Є–µ GHZ –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М –Ї–∞–Ї:
|
Ψ ќ® -->
⟩ вЯ© -->
G
H
Z
=
1
2
2
[
(
|
+
x
⟩ вЯ© -->
a
|
+
x
⟩ вЯ© -->
b
+
|
− вИТ -->
x
⟩ вЯ© -->
a
|
− вИТ -->
x
⟩ вЯ© -->
b
)
(
|
0
⟩ вЯ© -->
c
+
|
1
⟩ вЯ© -->
c
)
+
(
|
+
x
⟩ вЯ© -->
a
|
− вИТ -->
x
⟩ вЯ© -->
b
+
|
+
x
⟩ вЯ© -->
a
|
− вИТ -->
x
⟩ вЯ© -->
b
)
(
|
0
⟩ вЯ© -->
c
− вИТ -->
|
1
⟩ вЯ© -->
c
)
]
{\displaystyle |\mathrm {\Psi } \rangle _{\rm {GHZ}}={\frac {1}{2{\sqrt {2}}}}[({|+x\rangle _{a}|+x\rangle _{b}+|-x\rangle _{a}|-x\rangle _{b}})(|0\rangle _{c}+|1\rangle _{c})+({|+x\rangle _{a}|-x\rangle _{b}+|+x\rangle _{a}|-x\rangle _{b}})(|0\rangle _{c}-|1\rangle _{c})]}
–≥–і–µ (–∞, b, —Б) –Њ–±–Њ–Ј–љ–∞—З–∞—О—В —З–∞—Б—В–Є—Ж—Л (–і–ї—П –Р–ї–Є—Б—Л, –С–Њ–±–∞, –І–∞—А–ї–Є) –Є —Б–Њ—Б—В–Њ—П–љ–Є—П –Р–ї–Є—Б—Л –Є –С–Њ–±–∞ –Ј–∞–њ–Є—Б–∞–љ—Л –≤ X-–±–∞–Ј–Є—Б–µ. –Я—А–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є —В–∞–Ї–Њ–є —Д–Њ—А–Љ—Л –Ј–∞–њ–Є—Б–Є —Б—В–∞–љ–Њ–≤–Є—В—Б—П –Њ—З–µ–≤–Є–і–љ—Л–Љ, —З—В–Њ —Б—Г—Й–µ—Б—В–≤—Г–µ—В –Ї–Њ—А—А–µ–ї—П—Ж–Є—П –Љ–µ–ґ–і—Г –Є–Ј–Љ–µ—А–µ–љ–Є—П–Љ–Є –Р–ї–Є—Б—Л –Є –С–Њ–±–∞ –Є –Њ–і–љ–Њ—З–∞—Б—В–Є—З–љ—Л–Љ —Б–Њ—Б—В–Њ—П–љ–Є–µ–Љ –І–∞—А–ї–Є:
–Х—Б–ї–Є —Б–Њ—Б—В–Њ—П–љ–Є—П –Р–ї–Є—Б—Л –Є –С–Њ–±–∞ —Б–Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ–љ—Л, —В–Њ —Г –І–∞—А–ї–Є —Б–Њ—Б—В–Њ—П–љ–Є–µ
|
0
⟩ вЯ© -->
c
+
|
1
⟩ вЯ© -->
c
2
{\displaystyle {\frac {|0\rangle _{c}+|1\rangle _{c}}{\sqrt {2}}}}
|
0
⟩ вЯ© -->
c
− вИТ -->
|
1
⟩ вЯ© -->
c
2
{\displaystyle {\frac {|0\rangle _{c}-|1\rangle _{c}}{\sqrt {2}}}}
–Т–ї–Є—П–љ–Є–µ –Є–Ј–Љ–µ—А–µ–љ–Є–є –Р–ї–Є—Б—Л –Є –С–Њ–±–∞ –љ–∞ —Б–Њ—Б—В–Њ—П–љ–Є–µ –І–∞—А–ї–Є –і–ї—П —Б—В–∞–љ–і–∞—А—В–љ–Њ–≥–Њ GHZ-—Б–Њ—Б—В–Њ—П–љ–Є—П –Ш–Ј —В–∞–±–ї–Є—Ж—Л, —А–µ–Ј—О–Љ–Є—А—Г—О—Й–µ–є —Н—В–Є –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є, —П—Б–љ–Њ, —З—В–Њ –µ—Б–ї–Є –І–∞—А–ї–Є –Ј–љ–∞–µ—В –≤ –Ї–∞–Ї–Є—Е –±–∞–Ј–Є—Б–∞—Е –њ—А–Њ–≤–Њ–і–Є–ї–Є—Б—М –Є–Ј–Љ–µ—А–µ–љ–Є—П –Р–ї–Є—Б—Л –Є –С–Њ–±–∞, —В–Њ –Њ–љ –Љ–Њ–ґ–µ—В –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –Є–Ј–Љ–µ—А–µ–љ–Є–µ —Б–≤–Њ–µ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П, —З—В–Њ–±—Л –Њ–њ—А–µ–і–µ–ї–Є—В—М, –±—Л–ї–Є –ї–Є —Г –љ–Є—Е –Њ–і–Є–љ–∞–Ї–Њ–≤—Л–µ —А–µ–Ј—Г–ї—М—В–∞—В—Л –Є–ї–Є –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л–µ. –Э–Њ, —З—В–Њ–±—Л —Б–і–µ–ї–∞—В—М —Н—В–Њ—В –≤—Л–≤–Њ–і, –І–∞—А–ї–Є –і–Њ–ї–ґ–µ–љ –≤—Л–±—А–∞—В—М –њ—А–∞–≤–Є–ї—М–љ—Л–є –±–∞–Ј–Є—Б –і–ї—П –Є–Ј–Љ–µ—А–µ–љ–Є—П —Б–Њ–±—Б—В–≤–µ–љ–љ–Њ–є —З–∞—Б—В–Є—Ж—Л. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ–љ —Б–ї—Г—З–∞–є–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –≤—Л–±–Є—А–∞–µ—В –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П –љ–µ –Ї–Њ–Љ–Љ—Г—В–Є—А—Г—О—Й–Є–Љ–Є –±–∞–Ј–Є—Б–∞–Љ–Є, –Њ–љ –Љ–Њ–ґ–µ—В –Є–Ј–≤–ї–µ—З—М –њ–Њ–ї–µ–Ј–љ—Г—О –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—О —В–Њ–ї—М–Ї–Њ —Б –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О 50 %. –° —В–∞–Ї–Њ–є –ґ–µ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О —А–µ–Ј—Г–ї—М—В–∞—В—Л –љ–Є—З–µ–≥–Њ –љ–µ –і–∞—О—В –Є –і–Њ–ї–ґ–љ—Л –±—Л—В—М –Њ—В–±—А–Њ—И–µ–љ—Л. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –Ї–∞–Ї –≤–Є–і–љ–Њ –Є–Ј —В–∞–±–ї–Є—Ж—Л, –І–∞—А–ї–Є –љ–µ –Љ–Њ–ґ–µ—В –Њ–њ—А–µ–і–µ–ї–Є—В—М, –Ї—В–Њ –Є–Љ–µ–љ–љ–Њ —З—В–Њ –Є–Ј–Љ–µ—А—П–ї, —В–Њ–ї—М–Ї–Њ –±—Л–ї–Є –ї–Є —А–µ–Ј—Г–ї—М—В–∞—В—Л –Р–ї–Є—Б—Л –Є –С–Њ–±–∞ –Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ—Л –Є–ї–Є –∞–љ—В–Є–Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ—Л. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –µ–і–Є–љ—Б—В–≤–µ–љ–љ—Л–є —Б–њ–Њ—Б–Њ–± –і–ї—П –І–∞—А–ї–Є —Г–Ј–љ–∞—В—М, —З—В–Њ –±—Л–ї–Њ —Г –Р–ї–Є—Б—Л вАФ —А–∞–±–Њ—В–∞—В—М –≤–Љ–µ—Б—В–µ —Б –С–Њ–±–Њ–Љ –Є –Њ–±–Љ–µ–љ–Є–≤–∞—В—М—Б—П —Б –љ–Є–Љ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ–Є –Є–Ј–Љ–µ—А–µ–љ–Є–є. –Ґ–Њ–≥–і–∞ –Њ–љ–Є —Б–Љ–Њ–≥—Г—В –Є–Ј–≤–ї–µ—З—М —А–µ–Ј—Г–ї—М—В–∞—В—Л –Ї–∞–ґ–і–Њ–≥–Њ –Є–Ј–Љ–µ—А–µ–љ–Є—П –Р–ї–Є—Б—Л –Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —Н—В—Г –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—О –і–ї—П —Б–Њ–Ј–і–∞–љ–Є—П –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–ї—О—З–∞, –Ї–Њ—В–Њ—А—Л–є –Ј–љ–∞—О—В —В–Њ–ї—М–Ї–Њ –Њ–љ–Є.
–Я—А–Њ—Б—В–Њ–є —Б–ї—Г—З–∞–є —Б GHZ-—Б–Њ—Б—В–Њ—П–љ–Є–µ–Љ –Љ–Њ–ґ–µ—В –±—Л—В—М —А–∞—Б—И–Є—А–µ–љ —Б –њ–Њ–Љ–Њ—Й—М—О —Б–Є—Б—В–µ–Љ—Л –њ–Њ—А–Њ–≥–Њ–≤. –Т –њ–Њ—А–Њ–≥–Њ–≤–Њ–є —Б—Е–µ–Љ–µ ((k, n)) (–і–≤–Њ–є–љ—Л–µ —Б–Ї–Њ–±–Ї–Є –Њ–±–Њ–Ј–љ–∞—З–∞—О—В –Ї–≤–∞–љ—В–Њ–≤—Г—О —Б—Е–µ–Љ—Г), –Р–ї–Є—Б–∞ –і–µ–ї–Є—В —Б–≤–Њ–є —Б–µ–Ї—А–µ—В–љ—Л–є –Ї–ї—О—З (–Ї–≤–∞–љ—В–Њ–≤–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ) –љ–∞ n —Б–µ–Ї—А–µ—В–љ—Л—Е –Ї–ї—О—З–µ–є —В–∞–Ї, —З—В–Њ –µ—Б–ї–Є –≤–Ј—П—В—М –ї—О–±—Л–µ kвЙ§n –Ї–ї—О—З–µ–є, —В–Њ –±—Г–і–µ—В –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –Є–Ј–≤–ї–µ—З—М –њ–Њ–ї–љ—Г—О –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—О –Њ –Ї–ї—О—З–µ –Р–ї–Є—Б—Л, –∞ –µ—Б–ї–Є k-1 –Є–ї–Є –Љ–µ–љ—М—И–µ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Ї–ї—О—З–µ–є, —В–Њ –љ–µ—В. –І–Є—Б–ї–Њ –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї–µ–є k, –љ–µ–Њ–±—Е–Њ–і–Є–Љ—Л—Е –і–ї—П –Є–Ј–≤–ї–µ—З–µ–љ–Є—П —Б–µ–Ї—А–µ—В–∞, –Њ–≥—А–∞–љ–Є—З–µ–љ–Њ –љ–µ—А–∞–≤–µ–љ—Б—В–≤–Њ–Љ n /2 < k вЙ§ n
–Ф–Њ —В–µ—Е –њ–Њ—А, –њ–Њ–Ї–∞ —Б—Г—Й–µ—Б—В–≤—Г–µ—В –њ–Њ—А–Њ–≥–Њ–≤–∞—П —Б—Е–µ–Љ–∞ ((k ,n )) , –њ–Њ—А–Њ–≥–Њ–≤–∞—П —Б—Е–µ–Љ–∞ ((k ,n -1)) –Љ–Њ–ґ–µ—В –±—Л—В—М –њ–Њ–ї—Г—З–µ–љ–∞ –њ—Г—В–µ–Љ –њ—А–Њ—Б—В–Њ–≥–Њ –Њ—В–±—А–∞—Б—Л–≤–∞–љ–Є—П –Њ–і–љ–Њ–≥–Њ –Ї–ї—О—З–∞ (k –і–Њ–ї–ґ–љ–Њ –±—Л—В—М —Б—В—А–Њ–≥–Њ –Љ–µ–љ—М—И–µ n).
–°–ї–µ–і—Г—О—Й–∞—П —Б—Е–µ–Љ–∞ –Њ–њ–Є—Б—Л–≤–∞–µ—В –њ—А–Њ—Б—В—Г—О –њ–Њ—А–Њ–≥–Њ–≤—Г—О —Б—Е–µ–Љ—Г ((2,3))[ 5]
|
Ψ ќ® -->
⟩ вЯ© -->
a
=
α ќ± -->
|
0
⟩ вЯ© -->
+
β ќ≤ -->
|
1
⟩ вЯ© -->
+
γ ќ≥ -->
|
2
⟩ вЯ© -->
,
{\displaystyle |\mathrm {\Psi } \rangle _{a}=\alpha |0\rangle +\beta |1\rangle +\gamma |2\rangle ,}
–†–∞—Б–Ї—А–Њ–µ–Љ –µ–≥–Њ, –Ї–∞–Ї —В—А–Є –Ї—Г—В—А–Є—В–∞ :
|
ψ ѕИ -->
⟩ вЯ© -->
=
α ќ± -->
(
|
000
⟩ вЯ© -->
+
|
111
⟩ вЯ© -->
+
|
222
⟩ вЯ© -->
)
+
β ќ≤ -->
(
|
012
⟩ вЯ© -->
+
|
120
⟩ вЯ© -->
+
|
201
⟩ вЯ© -->
)
+
γ ќ≥ -->
(
|
021
⟩ вЯ© -->
+
|
102
⟩ вЯ© -->
+
|
210
⟩ вЯ© -->
)
{\displaystyle |\mathrm {\psi } \rangle =\alpha (|000\rangle +|111\rangle +|222\rangle )+\beta (|012\rangle +|120\rangle +|201\rangle )+\gamma (|021\rangle +|102\rangle +|210\rangle )}
–Є —А–∞–Ј–і–∞–і–Є–Љ –њ–Њ –Њ–і–љ–Њ–Љ—Г –Ї—Г—В—А–Є—В—Г –Ї–∞–ґ–і–Њ–Љ—Г –Є–Ј —В—А—С—Е —Г—З–∞—Б—В–љ–Є–Ї–Њ–≤. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –Њ–і–Є–љ –Ї–ї—О—З –љ–µ –і–∞—С—В –љ–Є–Ї–∞–Ї–Њ–є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є –Њ –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є –Р–ї–Є—Б—Л, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –Ї–∞–ґ–і—Л–є –љ–∞—Е–Њ–і–Є—В—Б—П –≤ –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ —Б–Љ–µ—И–∞–љ–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є. –Ґ–µ–Љ –љ–µ –Љ–µ–љ–µ–µ, –і–≤–∞ –Ї–ї—О—З–∞ –Љ–Њ–≥—Г—В –±—Л—В—М –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ—Л –і–ї—П —А–µ–Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–Є –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П. –Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З—В–Њ —Г –љ–∞—Б –µ—Б—В—М –њ–µ—А–≤—Л–µ –і–≤–∞ –Ї–ї—О—З–∞. –Ф–Њ–±–∞–≤–Є–Љ –њ–µ—А–≤—Л–є –Ї–ї—О—З –Ї–Њ –≤—В–Њ—А–Њ–Љ—Г (–њ–Њ –Љ–Њ–і—Г–ї—О —В—А–Є), –∞ –Ј–∞—В–µ–Љ –њ–Њ–ї—Г—З–Є–≤—И–µ–µ—Б—П –љ–Њ–≤–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ –і–Њ–±–∞–≤–Є–Љ –Ї –њ–µ—А–≤–Њ–Љ—Г –Ї–ї—О—З—Г. –Т –Є—В–Њ–≥–µ –њ–Њ–ї—Г—З–Є–Љ:
|
ψ ѕИ -->
⟩ вЯ© -->
=
(
α ќ± -->
|
0
⟩ вЯ© -->
+
β ќ≤ -->
|
1
⟩ вЯ© -->
+
γ ќ≥ -->
|
2
⟩ вЯ© -->
)
(
|
00
⟩ вЯ© -->
+
|
12
⟩ вЯ© -->
+
|
21
⟩ вЯ© -->
)
{\displaystyle |\mathrm {\psi } \rangle =(\alpha |0\rangle +\beta |1\rangle +\gamma |2\rangle )(|00\rangle +|12\rangle +|21\rangle )}
–≥–і–µ –њ–µ—А–≤—Л–є –Ї—Г—В—А–Є—В вАФ –≤ —В–Њ—З–љ–Њ—Б—В–Є –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ –Р–ї–Є—Б—Л. –° –њ–Њ–Љ–Њ—Й—М—О —Н—В–Њ–≥–Њ –Љ–µ—В–Њ–і–∞ –Є—Б—Е–Њ–і–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –≤–Њ—Б—Б—В–∞–љ–Њ–≤–ї–µ–љ–Њ –љ–∞ –Њ–і–љ–Њ–є –Є–Ј —З–∞—Б—В–Є—Ж, –Ї–Њ—В–Њ—А—Л–µ –Љ—Л —А–∞–Ј–і–∞–ї–Є, –љ–Њ –Њ—З–µ–љ—М –≤–∞–ґ–љ–Њ, —З—В–Њ–±—Л –≤ —Е–Њ–і–µ —Н—В–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –љ–µ –њ—А–Њ–Є–Ј–≤–Њ–і–Є–ї–Є—Б—М –љ–Є–Ї–∞–Ї–Є–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П, —З—В–Њ–±—Л –љ–µ –і–Њ–њ—Г—Б—В–Є—В—М –Ї–Њ–ї–ї–∞–њ—Б –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є.
–С–µ–Ј–Њ–њ–∞—Б–љ–Њ—Б—В—М –Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —А–∞–Ј–і–µ–ї–µ–љ–Є—П —Б–µ–Ї—А–µ—В–∞ –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ —В–µ–Њ—А–µ–Љ—Г –Њ –Ј–∞–њ—А–µ—В–µ –Ї–ї–Њ–љ–Є—А–Њ–≤–∞–љ–Є—П –і–ї—П –Ј–∞—Й–Є—В—Л –Њ—В –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –њ–µ—А–µ—Е–≤–∞—В–Њ–≤ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є. –≠—В–Њ—В —А–∞–Ј–і–µ–ї –њ–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞–µ—В –њ—А–Њ—В–Њ–Ї–Њ–ї –Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ –Ј–∞–њ—Г—В—Л–≤–∞–љ–Є—П –і–≤—Г—Е —З–∞—Б—В–Є—Ж, –Ї—А–∞—В–Ї–Њ —Г–њ–Њ–Љ—П–љ—Г—В—Л–є –≤—Л—И–µ.[ 7]
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –њ–Њ–і—Б–ї—Г—И–Є–≤–∞—О—Й–µ–≥–Њ, –Х–≤—Г, –Ї–Њ—В–Њ—А–∞—П, –Ї–∞–Ї –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —Б–њ–Њ—Б–Њ–±–љ–∞ –∞–±—Б–Њ–ї—О—В–љ–Њ —В–Њ—З–љ–Њ —А–∞—Б–њ–Њ–Ј–љ–∞–≤–∞—В—М –Є –≤–Њ—Б—Б–Њ–Ј–і–∞–≤–∞—В—М –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Б–Њ—Б—В–Њ—П–љ–Є—П, –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Л–µ –≤ –њ—А–Њ—В–Њ–Ї–Њ–ї–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —А–∞–Ј–і–µ–ї–µ–љ–Є—П —Б–µ–Ї—А–µ—В–∞. –¶–µ–ї—М –Х–≤—Л вАФ –њ–µ—А–µ—Е–≤–∞—В–Є—В—М –Њ–і–Є–љ –Є–Ј –Ї–ї—О—З–µ–є –њ–Њ–ї—Г—З–∞—В–µ–ї–µ–є (—Б–Ї–∞–ґ–µ–Љ, –С–Њ–±–∞), –Є–Ј–Љ–µ—А–Є—В—М –µ–≥–Њ, –Ј–∞—В–µ–Љ –≤–Њ—Б—Б–Њ–Ј–і–∞—В—М —Н—В–Њ —Б–Њ—Б—В–Њ—П–љ–Є–µ –Є –Њ—В–њ—А–∞–≤–Є—В—М –і–∞–ї—М—И–µ –њ–Њ –љ–∞–Ј–љ–∞—З–µ–љ–Є—О. –Я—А–Њ–±–ї–µ–Љ–∞ –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —В–Њ–Љ, —З—В–Њ –Х–≤–µ –љ—Г–ґ–љ–Њ —Б–ї—Г—З–∞–є–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –≤—Л–±—А–∞—В—М –±–∞–Ј–Є—Б –і–ї—П –Є–Ј–Љ–µ—А–µ–љ–Є—П, –Є –≤ –њ–Њ–ї–Њ–≤–Є–љ–µ —Б–ї—Г—З–∞–µ–≤ –Њ–љ–∞ –±—Г–і–µ—В –≤—Л–±–Є—А–∞—В—М –љ–µ–≤–µ—А–љ—Л–є. –Х—Б–ї–Є –Њ–љ–∞ –≤—Л–±–µ—А–µ—В –њ—А–∞–≤–Є–ї—М–љ—Л–є –±–∞–Ј–Є—Б, –Њ–љ–∞ —Б —Г–≤–µ—А–µ–љ–љ–Њ—Б—В—М—О –њ–Њ–ї—Г—З–Є—В –њ—А–∞–≤–Є–ї—М–љ—Л–є —А–µ–Ј—Г–ї—М—В–∞—В –Є —Б–Љ–Њ–ґ–µ—В –≤–Њ—Б—Б–Њ–Ј–і–∞—В—М –Є—Б—Е–Њ–і–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ –Ї–ї—О—З–∞, –Ї–Њ—В–Њ—А–Њ–µ –Њ–љ–∞ –Є–Ј–Љ–µ—А–Є–ї–∞, —З—В–Њ–±—Л –Њ—В–њ—А–∞–≤–Є—В—М –µ–≥–Њ –Њ–±—А–∞—В–љ–Њ –С–Њ–±—Г. –Ю–і–љ–∞–Ї–Њ, –µ—Б–ї–Є –Њ–љ–∞ –≤—Л–±–µ—А–µ—В –љ–µ–≤–µ—А–љ—Л–є –±–∞–Ј–Є—Б, —В–Њ –Њ—В–њ—А–∞–≤–Є—В –Њ–і–љ–Њ –Є–Ј –і–≤—Г—Е —Б–Њ—Б—В–Њ—П–љ–Є–є –і—А—Г–≥–Њ–≥–Њ –±–∞–Ј–Є—Б–∞. –Ъ–Њ–≥–і–∞ –С–Њ–± –Є–Ј–Љ–µ—А–Є—В –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ –Њ—В –Р–ї–Є—Б—Л –ї–Њ–ґ–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ, —В–Њ —Б –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О 50 % –Њ–љ –≤—Б–µ-—В–∞–Ї–Є –њ–Њ–ї—Г—З–Є—В –њ—А–∞–≤–Є–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ, —В–∞–Ї –Ї–∞–Ї —Б–Њ—Б—В–Њ—П–љ–Є–µ –≤ –љ–µ–њ—А–∞–≤–Є–ї—М–љ–Њ–Љ –±–∞–Ј–Є—Б–µ —П–≤–ї—П–µ—В—Б—П —Б—Г–њ–µ—А–њ–Њ–Ј–Є—Ж–Є–µ–є –і–≤—Г—Е —Б–Њ—Б—В–Њ—П–љ–Є–є –≤ –њ—А–∞–≤–Є–ї—М–љ–Њ–Љ –±–∞–Ј–Є—Б–µ. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Н—В–Њ –≤–Љ–µ—И–∞—В–µ–ї—М—Б—В–≤–Њ —Б–Њ —Б—В–Њ—А–Њ–љ—Л –Х–≤—Л —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В –Њ—И–Є–±–Ї—Г –≤ –њ—А–Њ—В–Њ–Ї–Њ–ї–µ –љ–∞ 25 %. –Я—А–Є –і–Њ—Б—В–∞—В–Њ—З–љ–Њ–Љ –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ –Є–Ј–Љ–µ—А–µ–љ–Є–є –±—Г–і–µ—В –њ–Њ—З—В–Є –љ–µ–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –њ—А–Њ–њ—Г—Б—В–Є—В—М –Њ—И–Є–±–Ї–Є –њ—А–Њ—В–Њ–Ї–Њ–ї–∞, –≤–Њ–Ј–љ–Є–Ї–∞—О—Й–Є–µ —Б –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О 75 % –≤–Љ–µ—Б—В–Њ 50 %, –њ—А–µ–і—Б–Ї–∞–Ј–∞–љ–љ—Л—Е —В–µ–Њ—А–Є–µ–є, —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –Љ–Њ–ґ–љ–Њ –њ–Њ–љ—П—В—М, —З—В–Њ –≤ –Ї–∞–љ–∞–ї–µ —Б–≤—П–Ј–Є –µ—Б—В—М –њ–Њ–і—Б–ї—Г—И–Є–≤–∞—О—Й–Є–є.
–С–Њ–ї–µ–µ —Б–ї–Њ–ґ–љ—Л–µ —Б—В—А–∞—В–µ–≥–Є–Є –њ–Њ–і—Б–ї—Г—И–Є–≤–∞–љ–Є—П –Љ–Њ–≥—Г—В –±—Л—В—М –≤—Л–њ–Њ–ї–љ–µ–љ—Л —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е —Б–Њ—Б—В–Њ—П–љ–Є–є, –љ–Њ –њ–Њ–і—Б–ї—Г—И–Є–≤–∞—О—Й–Є–є –≤—Б–µ —А–∞–≤–љ–Њ –±—Г–і–µ—В –Њ–±–љ–∞—А—Г–ґ–µ–љ –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ.
–Ґ–µ–њ–µ—А—М —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–ї—Г—З–∞–є, –Ї–Њ–≥–і–∞ –Њ–і–Є–љ –Є–Ј —Г—З–∞—Б—В–љ–Є–Ї–Њ–≤ –њ—А–Њ—В–Њ–Ї–Њ–ї–∞ (—Б–Ї–∞–ґ–µ–Љ, –С–Њ–±) –і–µ–є—Б—В–≤—Г–µ—В –Ї–∞–Ї –Ј–ї–Њ—Г–Љ—Л—И–ї–µ–љ–љ–Є–Ї, –њ—Л—В–∞—П—Б—М –њ–Њ–ї—Г—З–Є—В—М —Б–µ–Ї—А–µ—В –±–µ–Ј –≤–µ–і–Њ–Љ–∞ –і—А—Г–≥–Є—Е —Г—З–∞—Б—В–љ–Є–Ї–Њ–≤. –Я—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞–≤ –≤–Њ–Ј–љ–Є–Ї–∞—О—Й–Є–µ –Ј–і–µ—Б—М —А–∞–Ј–ї–Є—З–љ—Л–µ —Б–Є—В—Г–∞—Ж–Є–Є, –Љ–Њ–ґ–љ–Њ –њ—А–Є–є—В–Є –Ї –≤—Л–≤–Њ–і—Г, —З—В–Њ –≤—Л–±–Њ—А–Њ–Љ –љ–∞–і–ї–µ–ґ–∞—Й–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –і–µ–є—Б—В–≤–Є–є, –≤ –Ї–Њ—В–Њ—А–Њ–Љ –С–Њ–± –Є –І–∞—А–ї–Є –Њ–±–Љ–µ–љ–Є–≤–∞—О—В—Б—П —Б–≤–Њ–Є–Љ–Є —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ–Є –њ—А–Є —В–µ—Б—В–Є—А–Њ–≤–∞–љ–Є–Є –љ–∞ –њ–Њ–і—Б–ї—Г—И–Є–≤–∞–љ–Є–µ, –Љ–Њ–ґ–љ–Њ –≥–∞—А–∞–љ—В–Є—А–Њ–≤–∞—В—М –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є–µ –ї—О–±–Њ–≥–Њ –Њ–±–Љ–∞–љ–∞, –Ї–Њ—В–Њ—А—Л–є –Љ–Њ–ґ–µ—В –Є–Љ–µ—В—М –Ј–і–µ—Б—М –Љ–µ—Б—В–Њ. –Я—А–∞–≤–Є–ї—М–љ—Л–є –њ–Њ—А—П–і–Њ–Ї —В–∞–Ї–Њ–є:
–Я–Њ–ї—Г—З–∞—В–µ–ї—М 1 –Њ—В–і–∞—С—В —А–µ–Ј—Г–ї—М—В–∞—В—Л —Б–≤–Њ–µ–≥–Њ –Є–Ј–Љ–µ—А–µ–љ–Є—П.
–Я–Њ–ї—Г—З–∞—В–µ–ї—М 2 –Њ—В–і–∞—С—В —А–µ–Ј—Г–ї—М—В–∞—В—Л —Б–≤–Њ–µ–≥–Њ –Є–Ј–Љ–µ—А–µ–љ–Є—П.
–Я–Њ–ї—Г—З–∞—В–µ–ї—М 2 —Б–Њ–Њ–±—Й–∞–µ—В –≤ –Ї–∞–Ї–Њ–Љ –±–∞–Ј–Є—Б–µ –њ—А–Њ–≤–Њ–і–Є–ї–Є—Б—М –Є–Ј–Љ–µ—А–µ–љ–Є—П.
–Я–Њ–ї—Г—З–∞—В–µ–ї—М 1 —Б–Њ–Њ–±—Й–∞–µ—В –≤ –Ї–∞–Ї–Њ–Љ –±–∞–Ј–Є—Б–µ –њ—А–Њ–≤–Њ–і–Є–ї–Є—Б—М –Є–Ј–Љ–µ—А–µ–љ–Є—П. –Ґ–∞–Ї–Њ–є –њ–Њ—А—П–і–Њ–Ї –љ–µ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –њ–Њ–ї—Г—З–∞—В–µ–ї—О 2 —Г–Ј–љ–∞—В—М, –≤ –Ї–∞–Ї–Њ–Љ –±–∞–Ј–Є—Б–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ—В–њ—А–∞–≤–ї—П—В—М –Є–Ј–Љ–µ—А–µ–љ–Є—П, —З—В–Њ–±—Л –Њ–±–Љ–∞–љ—Г—В—М –і—А—Г–≥–Є—Е —Г—З–∞—Б—В–љ–Є–Ї–Њ–≤, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –њ–Њ–ї—Г—З–∞—В–µ–ї—М 2 –µ—Й—С –љ–µ –Ј–љ–∞–µ—В, –Ї–∞–Ї–Њ–є –±–∞–Ј–Є—Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї –њ–Њ–ї—Г—З–∞—В–µ–ї—М 1. –Р–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ–ї—Г—З–∞—В–µ–ї—М 1 –і–Њ–ї–ґ–µ–љ —Б–љ–∞—З–∞–ї–∞ –Њ—В–њ—А–∞–≤–Є—В—М —Б–≤–Њ–Є —А–µ–Ј—Г–ї—М—В–∞—В—Л, –Њ–љ –љ–µ –Љ–Њ–ґ–µ—В –њ–Њ–љ—П—В—М, –і–Њ–ї–ґ–љ—Л –ї–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П –±—Л—В—М –Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є –Є–ї–Є –∞–љ—В–Є–Ї–Њ–Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є –і–ї—П –њ—А–∞–≤–Є–ї—М–љ–Њ–є –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Є —Б –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Л–Љ–Є –і—А—Г–≥–Є–Љ–Є –±–∞–Ј–Є—Б–∞–Љ–Є. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –љ–µ—З–µ—Б—В–љ—Л–µ –і–µ–є—Б—В–≤–Є—П –±—Г–і—Г—В —Б–Њ–Ј–і–∞–≤–∞—В—М –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–µ –Њ—И–Є–±–Ї–Є –љ–∞ —Н—В–∞–њ–µ –њ—А–Њ–≤–µ—А–Ї–Є –љ–∞ –њ–Њ–і—Б–ї—Г—И–Є–≤–∞–љ–Є–µ, –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ –Њ—В —В–Њ–≥–Њ, —П–≤–ї—П–µ—В—Б—П –ї–Є –Ј–ї–Њ—Г–Љ—Л—И–ї–µ–љ–љ–Є–Ї–Њ–Љ –њ–Њ–ї—Г—З–∞—В–µ–ї—М 1 –Є–ї–Є –њ–Њ–ї—Г—З–∞—В–µ–ї—М 2. –Я–Њ—Н—В–Њ–Љ—Г –њ–Њ—А—П–і–Њ–Ї –Њ—В–њ—А–∞–≤–ї–µ–љ–Є—П –і–∞–љ–љ—Л—Е –і–Њ–ї–ґ–µ–љ –±—Л—В—М —В—Й–∞—В–µ–ї—М–љ–Њ –≤—Л–±—А–∞–љ, —З—В–Њ–±—Л –љ–µ –і–∞—В—М –љ–µ—З–µ—Б—В–љ–Њ–Љ—Г –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—О –њ–Њ–ї—Г—З–Є—В—М —Б–µ–Ї—А–µ—В –Є –Њ—Б—В–∞—В—М—Б—П –љ–µ–Ј–∞–Љ–µ—З–µ–љ–љ—Л–Љ –і–ї—П –і—А—Г–≥–Є—Е —Г—З–∞—Б—В–љ–Є–Ї–Њ–≤.
–Я–µ—А–≤–∞—П —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–∞—П –і–µ–Љ–Њ–љ—Б—В—А–∞—Ж–Є—П –Ъ–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —А–∞–Ј–і–µ–ї–µ–љ–Є—П —Б–µ–Ї—А–µ—В–∞ –±—Л–ї–∞ –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤ 2001 –≥–Њ–і—Г. –Ю–љ–∞ —Б—В–∞–ї–∞ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ–є –±–ї–∞–≥–Њ–і–∞—А—П –і–Њ—Б—В–Є–ґ–µ–љ–Є—П–Љ –≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Њ–њ—В–Є–Ї–µ [ 8]
–Я–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–∞—П –Є–і–µ—П –і–ї—П –Ъ–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —А–∞–Ј–і–µ–ї–µ–љ–Є—П –Ї–ї—О—З–µ–є —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–є GHZ –±—Л–ї–∞ –Њ—З–µ–љ—М —Б–ї–Њ–ґ–љ–Њ–є –і–ї—П —А–µ–∞–ї–Є–Ј–∞—Ж–Є–Є –Є–Ј-–Ј–∞ —В—А—Г–і–љ–Њ—Б—В–µ–є –≤ –њ–Њ–ї—Г—З–µ–љ–Є–Є —В—А—С—Е —Б–Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ–љ—Л—Е —З–∞—Б—В–Є—Ж. –Я—А–µ–і–ї–∞–≥–∞–ї–Њ—Б—М —Б–і–µ–ї–∞—В—М —Н—В–Њ –ї–Є–±–Њ —З–µ—А–µ–Ј –њ–∞—А–∞–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ —А–∞—Б—Б–µ—П–љ–Є–µ —Б
χ ѕЗ -->
3
{\displaystyle \chi ^{3}}
[ 9] —Б–њ–Њ–љ—В–∞–љ–љ–Њ–≥–Њ –њ–∞—А–∞–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б—Б–µ—П–љ–Є—П —Б
χ ѕЗ -->
2
{\displaystyle \chi ^{2}}
–Њ–њ—В–Є—З–µ—Б–Ї–Њ–є –љ–∞–Ї–∞—З–Ї–Њ–є .
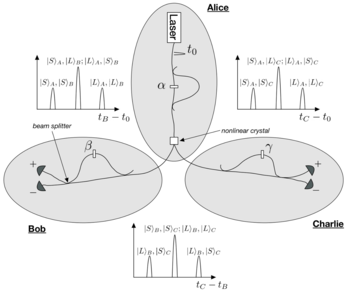
–Ф–≤—Г—Е—Д–Њ—В–Њ–љ–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —А–∞–Ј–і–µ–ї–µ–љ–Є–µ —Б–µ–Ї—А–µ—В–∞ —Б –њ–Њ–Љ–Њ—Й—М—О —Б–њ–Њ–љ—В–∞–љ–љ–Њ–≥–Њ –њ–∞—А–∞–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б—Б–µ—П–љ–Є—П . –≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–∞—П —Г—Б—В–∞–љ–Њ–≤–Ї–∞ —А–∞–±–Њ—В–∞–µ—В —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
–Р–ї–Є—Б–∞: –Є–Љ–њ—Г–ї—М—Б–љ—Л–є –ї–∞–Ј–µ—А, –Є–Ј–ї—Г—З–∞–µ—В –≤ –Љ–Њ–Љ–µ–љ—В –≤—А–µ–Љ–µ–љ–Є
t
0
{\displaystyle t_{0}}
α ќ± -->
.
{\displaystyle \alpha .}
–С–Њ–± –Є –І–∞—А–ї–Є: –Њ–±–∞ –Є–Љ–µ—О—В –Є–љ—В–µ—А—Д–µ—А–Њ–Љ–µ—В—А—Л, –Є–і–µ–љ—В–Є—З–љ—Л–µ —В–Њ–Љ—Г, —З—В–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–∞ –Р–ї–Є—Б–∞, –њ–Њ—Н—В–Њ–Љ—Г –і–Њ—Б—В–Є–≥–∞–µ—В—Б—П –∞–±—Б–Њ–ї—О—В–љ–Њ —В–∞–Ї–∞—П –ґ–µ —А–∞–Ј–љ–Є—Ж–∞ –≤–Њ –≤—А–µ–Љ–µ–љ–Є –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П –њ–ї–µ—З–∞–Љ–Є. –Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ –Ї–∞–ґ–і—Л–є –Є–Љ–µ–µ—В —Д–∞–Ј–Њ–≤—А–∞—Й–∞—В–µ–ї—М, –Њ–±–Њ–Ј–љ–∞—З–∞–µ–Љ—Л–є
β ќ≤ -->
{\displaystyle \beta }
γ ќ≥ -->
{\displaystyle \gamma }
t
B
{\displaystyle t_{B}}
t
C
{\displaystyle t_{C}}
–Ш—Б–њ–Њ–ї—М–Ј—Г–µ–Љ —Б–ї–µ–і—Г—О—Й–µ–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ –њ—Г—В–Є –Њ–±–Љ–µ–љ–∞ —Д–Њ—В–Њ–љ–∞–Љ–Є:
|
X
⟩ вЯ© -->
i
,
|
Y
⟩ вЯ© -->
j
{\displaystyle |\mathrm {X} \rangle _{i},|\mathrm {Y} \rangle _{j}}
|
S
⟩ вЯ© -->
A
,
|
L
⟩ вЯ© -->
j
{\displaystyle |\mathrm {S} \rangle _{A},|\mathrm {L} \rangle _{j}}
|
L
⟩ вЯ© -->
A
,
|
S
⟩ вЯ© -->
j
{\displaystyle |\mathrm {L} \rangle _{A},|\mathrm {S} \rangle _{j}}
|
S
⟩ вЯ© -->
B
,
|
S
⟩ вЯ© -->
C
{\displaystyle |\mathrm {S} \rangle _{B},|\mathrm {S} \rangle _{C}}
|
L
⟩ вЯ© -->
B
,
|
L
⟩ вЯ© -->
C
{\displaystyle |\mathrm {L} \rangle _{B},|\mathrm {L} \rangle _{C}}
|
ψ ѕИ -->
⟩ вЯ© -->
=
1
2
(
|
L
⟩ вЯ© -->
A
,
|
S
⟩ вЯ© -->
B
|
S
⟩ вЯ© -->
C
+
e
i
(
α ќ± -->
+
β ќ≤ -->
+
γ ќ≥ -->
)
|
S
⟩ вЯ© -->
A
,
|
L
⟩ вЯ© -->
B
|
L
⟩ вЯ© -->
C
)
)
{\displaystyle |\mathrm {\psi } \rangle ={\frac {1}{\sqrt {2}}}(|L\rangle _{A},|S\rangle _{B}|S\rangle _{C}+e^{i(\alpha +\beta +\gamma )}|S\rangle _{A},|L\rangle _{B}|L\rangle _{C}))}
–≠—В–Њ —Б–Њ—Б—В–Њ—П–љ–Є–µ –Љ–Њ–ґ–љ–Њ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М –Ї–∞–Ї ¬Ђ–њ—Б–µ–≤–і–Њ-GHZ-—Б–Њ—Б—В–Њ—П–љ–Є–µ¬ї, –≤ –Ї–Њ—В–Њ—А–Њ–Љ –Њ—В–ї–Є—З–Є–µ –Њ—В –Є—Б—В–Є–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П GHZ –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —В–Њ–Љ, —З—В–Њ —В—А–Є —Д–Њ—В–Њ–љ–∞ –љ–µ —Б—Г—Й–µ—Б—В–≤—Г—О—В –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ. –Ґ–µ–Љ –љ–µ –Љ–µ–љ–µ–µ, —В—А–Њ–є–љ–Њ–µ ¬Ђ—Б–Њ–≤–њ–∞–і–µ–љ–Є–µ¬ї –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ–Є—Б–∞–љ–Њ —В–Њ—З–љ–Њ —В–∞–Ї–Њ–є –ґ–µ –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є, –Ї–∞–Ї –і–ї—П –Є—Б—В–Є–љ–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П GHZ.
P
i
,
j
,
k
=
1
8
(
1
+
i
j
k
cos
вБ° -->
(
α ќ± -->
+
β ќ≤ -->
+
γ ќ≥ -->
)
)
{\displaystyle P_{i,j,k}={\frac {1}{8}}(1+ijk\cos(\alpha +\beta +\gamma ))}
–Я–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞–µ—В—Б—П, —З—В–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —А–∞–Ј–і–µ–ї–µ–љ–Є–µ –Ї–ї—О—З–µ–є –±—Г–і–µ—В —А–∞–±–Њ—В–∞—В—М —В–Њ—З–љ–Њ —В–∞–Ї –ґ–µ –і–ї—П —Н—В–Њ–≥–Њ –і–≤—Г—Е-—З–∞—Б—В–Є—З–љ–Њ–≥–Њ –Є—Б—В–Њ—З–љ–Є–Ї–∞.
–£—Б—В–∞–љ–Њ–≤–Є–≤ —Д–∞–Ј—Л
α ќ± -->
,
β ќ≤ -->
,
{\displaystyle \alpha ,\beta ,}
γ ќ≥ -->
{\displaystyle \gamma }
π ѕА -->
2
{\displaystyle {\frac {\pi }{2}}}
–љ–µ—А–∞–≤–µ–љ—Б—В–≤–∞ –С–µ–ї–ї–∞ –і–ї—П —В—А—С—Е —З–∞—Б—В–Є—Ж:
S
3
=
|
E
(
α ќ± -->
′
+
β ќ≤ -->
+
γ ќ≥ -->
)
+
E
(
α ќ± -->
+
β ќ≤ -->
′
+
γ ќ≥ -->
)
+
E
(
α ќ± -->
+
β ќ≤ -->
+
γ ќ≥ -->
′
)
− вИТ -->
E
(
α ќ± -->
′
+
β ќ≤ -->
′
+
γ ќ≥ -->
′
)
|
≤ вЙ§ -->
2
{\displaystyle S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}}
–≥–і–µ
E
(
α ќ± -->
+
β ќ≤ -->
+
γ ќ≥ -->
)
{\displaystyle E(\alpha +\beta +\gamma )}
(
α ќ± -->
,
β ќ≤ -->
,
γ ќ≥ -->
)
{\displaystyle (\alpha ,\beta ,\gamma )}
S
e
x
p
=
3.69
{\displaystyle S_{\rm {exp}}=3.69}
–≠—В–Њ—В –Њ—Б–љ–Њ–≤–Њ–њ–Њ–ї–∞–≥–∞—О—Й–Є–є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В –њ–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ –Ї–≤–∞–љ—В–Њ–≤—Л–µ –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Є–Ј —Н—В–Њ–є —Г—Б—В–∞–љ–Њ–≤–Ї–Є –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ –Њ–њ–Є—Б—Л–≤–∞—О—В—Б—П —Д—Г–љ–Ї—Ж–Є–µ–є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є
P
i
,
j
,
k
{\displaystyle P_{i,j,k}}
вЖС Shamir, Adi (1 November 1979). "How to share a secret" (PDF) . Communications of the ACM . 22 (11): 612вАФ613. doi :10.1145/359168.359176 . S2CID 16321225 . –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ (PDF) 10 –∞–≤–≥—Г—Б—В–∞ 2017 . вЖС Blakley, G.R. (1979). "Safeguarding Cryptographic Keys" (PDF) . Managing Requirements Knowledge, International Workshop on (AFIPS) . 48 : 313вАФ317. doi :10.1109/AFIPS.1979.98 . S2CID 38199738 . –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ –Є–Ј –Њ—А–Є–≥–Є–љ–∞–ї–∞ (PDF) 28 –Є—О–љ—П 2018 . вЖС Hillery, Mark; Bu≈Њek, Vladim√≠r; Berthiaume, Andr√© (1998). "Quantum Secret Sharing" (PDF) . Physical Review A . 59 (3): 1829вАФ1834. doi :10.1103/PhysRevA.59.1829 . –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ (PDF) 14 –і–µ–Ї–∞–±—А—П 2021 . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 14 –і–µ–Ї–∞–±—А—П 2021 . вЖС Gottesman, Daniel (2000). "Theory of quantum secret sharing" . Physical Review A . 61 (4): 042311. doi :10.1103/PhysRevA.61.042311 . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 14 –і–µ–Ї–∞–±—А—П 2021 . вЖС 1 2 Cleve, Richard; Gottesman, Daniel; Lo, Hoi-Kwong (1999). "How to share a quantum secret" (PDF) . Physical Review Letters . 83 (3): 648вАФ651. doi :10.1103/PhysRevLett.83.648 . –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ (PDF) 5 –і–µ–Ї–∞–±—А—П 2022 . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 14 –і–µ–Ї–∞–±—А—П 2021 . вЖС Wiesner, Stephen (January 1983). "Conjugate coding" . ACM SIGACT News . 15 (1): 78вАФ88. doi :10.1145/1008908.1008920 . –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ 4 –і–µ–Ї–∞–±—А—П 2022 . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 16 –і–µ–Ї–∞–±—А—П 2021 . вЖС 1 2 Karlsson, Anders; Koashi, Masato; Imoto, Nobuyuki (1999). "Quantum entanglement for secret sharing and secret splitting" . Physical Review A . 59 (1): 162вАФ168. doi :10.1103/PhysRevA.59.162 . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 14 –і–µ–Ї–∞–±—А—П 2021 . вЖС Tittel, W.; Zbinden, H.; Gisin, N. (2001). "Experimental demonstration of quantum secret sharing" . Physical Review A . 63 (4): 042301. doi :10.1103/PhysRevA.63.042301 . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 15 –і–µ–Ї–∞–±—А—П 2021 . вЖС ≈їukowski, M.; Zeilinger, A.; Horne, M.A.; Weinfurter, H. (1998). "Quest for GHZ states" (PDF) . Acta Physica Polonica A . 98 (1): 187вАФ195. –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ (PDF) 15 –Є—О–љ—П 2022 . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 15 –і–µ–Ї–∞–±—А—П 2021 .
























![{\displaystyle |\mathrm {\Psi } \rangle _{\rm {GHZ}}={\frac {1}{2{\sqrt {2}}}}[({|+x\rangle _{a}|+x\rangle _{b}+|-x\rangle _{a}|-x\rangle _{b}})(|0\rangle _{c}+|1\rangle _{c})+({|+x\rangle _{a}|-x\rangle _{b}+|+x\rangle _{a}|-x\rangle _{b}})(|0\rangle _{c}-|1\rangle _{c})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02e85aeaf2b26146fa63593cb3951694d090dcc1)