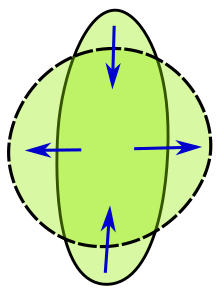
Изопериметрическая задача
|
Read other articles:

Yves Bissouma Bissouma bermain untuk Brighton & Hove Albion pada 2018Informasi pribadiNama lengkap Yves Bissouma[1]Tanggal lahir 30 Agustus 1996 (umur 27)[2]Tempat lahir Issia, Pantai GadingTinggi 1,81 m (5 ft 11+1⁄2 in)[2]Posisi bermain Gelandang BertahanInformasi klubKlub saat ini Tottenham HotspurNomor 8Karier junior Majestic SC2009–2014 JMG Academy BamakoKarier senior*Tahun Tim Tampil (Gol)2014–2016 AS Real Bamako 2016–2017 Lille...

Fictional character Fictional character William BludworthFinal Destination characterTony Todd as William Bludworth, as depicted in Final Destination 5First appearanceFinal DestinationLast appearanceFinal Destination 5Created byJeffrey ReddickPortrayed byTony ToddIn-universe informationOccupationCoronerLocationMt. Abraham, New York North Bay, New YorkStatusAlive William Bludworth is a fictional character in the Final Destination film series, portrayed by Tony Todd. He appears in Final Destinat...

This article is part of a series on theBudget and debt in theUnited States of America Major dimensions Economy Expenditures Federal budget Financial position Military budget Public debt Taxation Unemployment Total gov't spending Programs Medicare Social programs Social Security Contemporary issues Bowles–Simpson Commission Bush tax cuts Debt ceiling history Deficit reduction Fiscal cliff Healthcare reform Political debates Social Security debate Starve the beast Subprime mortgage crisis 2007

German clock maker This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nikolaus Lilienfeld – news · newspapers · books · scholar · JSTOR (February 2021) (Learn how and when to remove this template message) Nikolaus Lilienfeld Astronomical clock in the St. Nicholas Church, Stralsund Nikolaus Lilienfeld (also Nico...

Cerro Pan de Azúcar Cumbre del Pan de AzúcarLocalización geográficaCordillera Andes-Valle de AburráLocalización administrativaPaís ColombiaLocalización Medellín, Colombia ColombiaCaracterísticas generalesTipo CerroAltitud 2138 m s. n. m.Mapa de localización[editar datos en Wikidata] El cerro Pan de Azúcar es una formación rocosa ubicada en el centroriente de la ciudad Medellín, Antioquia, fue el punto clave para empezar la construcción de la Villa de la Can...

Portal Geschichte | Portal Biografien | Aktuelle Ereignisse | Jahreskalender | Tagesartikel ◄ | 10. Jahrhundert | 11. Jahrhundert | 12. Jahrhundert | ► ◄ | 1020er | 1030er | 1040er | 1050er | 1060er | 1070er | 1080er | ► ◄◄ | ◄ | 1054 | 1055 | 1056 | 1057 | 1058 | 1059 | 1060 | 1061 | 1062 | ► | ►► Staatsoberhäupter · Nekrolog Kalenderübersicht 1058 Januar Kw Mo Di Mi Do Fr Sa So 1 1 2 3 4 2 5 6 7 8 9 10 ...

التأثيرات العصبية والحيوية للتمارين الرياضية تعديل مصدري - تعديل تولد التمرينات الرياضية تأثيرات عصبية وحيوية عديدة متضمنةً مدىً واسعًا من التأثيرات على التركيبة البنائية للدماغ ووظائفه وعلى الإدراك المعرفي.[1][2][3][4] أثبتت الكثير من البحوث المجرا...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of FIFA World Cup final stadiums – news · newspapers · books · scholar · JSTOR (March 2020) (Learn how and when to remove this template message) There have been 21 editions of the FIFA World Cup which is an international association football tournament est...

Episode in the life of Jesus Transfiguration of Christ redirects here. For paintings with this name, see Transfiguration of Jesus in Christian art § Paintings with articles. The Transfiguration by Raphael, c. 1520 Events in theLife of Jesusaccording to the canonical gospels Early life Annunciation Visitation Nativity Virgin birth Adoration of the Shepherds Circumcision Presentation Adoration of the Magi Flight into Egypt Massacre of the Innocents Return to Nazareth Finding in the Temple...

American animated television series (2007–2010) ChowderGenre Adventure Fantasy Surreal comedy[1] Created byC. H. GreenblattDirected by Juli Hashiguchi Eddy Houchins Kris Sherwood Shaun Cashman Majella Milne Mike Milo Creative directorWilliam ReissVoices of Nicky Jones Dwight Schultz John DiMaggio Tara Strong C. H. Greenblatt Dana Snyder Liliana Mumy Mindy Sterling Theme music composer C. H. Greenblatt Dan Boer Zac Pike Composers Dan Boer Zac Pike Country of originUnited StatesOrigin...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Godzilla Island – news · newspapers · books · scholar · JSTOR (July 2021) (Learn how and when to remove this template message) Japanese TV series or program Godzilla IslandTitle cardGenreTokusatsuKaijuSuperheroScience fictionDeveloped byTohoWritten byTakah...

この項目では、器官の一つについて説明しています。二十八宿の一つについては「胃宿」をご覧ください。 胃 胃の解剖1:食道 2:ヒス角 3:噴門 4:胃角 5:幽門 6:十二指腸 A:胃底部 B:胃体部 C:前庭部 X:小彎 Y:大彎 1.胃体部(en:Body of stomach) 2.胃底部(en:Fundus) 3.前庭部(en:Anterior wall) 4.大彎(en:Greater curvature) 5.小彎(en:Lesser curvature) 6.噴門(en:Cardia) 9.幽門括約筋(en:Pyloric sphincter) 10.幽門洞(...

SirJohn Spencer LoginBorn9 November 1809Stromness, Orkney, United KingdomDied18 October 1863Felixstowe, Suffolk, United KingdomNationalityBritishEducationUniversity of EdinburghOccupation(s)Surgeon, Royal NavyKnown forGuardianship of Maharajah Duleep Singh and Koh-i-NoorSpouseLena Campbell Sir John Spencer Login (9 November 1809 – 18 October 1863) was a Scottish surgeon in British India, best remembered as the guardian of Maharajah Duleep Singh and the Koh-i-Noor diamond following the ...

Soviet class of destroyer leaders Soviet destroyer Kiev redirects here. For the Leningrad-class destroyer, see Soviet destroyer leader Kiev. For other classes of ships, see Kiev class. For other ships, see Kiev (ship). Line drawings to different scales of the never-completed Kiev-class destroyers; Project 48 (top), Project 48-K (bottom) Class overview Operators Soviet Navy Preceded byTashkent class Succeeded byNone Built1939–1941 Planned14 Completed0 Cancelled11 Scrapped3 General ...

District in Aqmola Region, KazakhstanArshalyDistrictArşaly audanyCountry KazakhstanRegionAqmola RegionAdministrative centerArshalyFounded1930Government • AkimAidar Itemgenovich Baymanov[1]Area • Total2,200 sq mi (5,800 km2)Population (2013)[2] • Total27,119Time zoneUTC+6 (East) Arshaly District (Kazakh: Аршалы ауданы, Arşaly audany) is a district of Akmola Region in northern Kazakhstan. The administrati...

Private university in Uttar Pradesh, IndiaThis article is about a private university established in Mathura. For the state university established in Lucknow, see Bhatkhande Sanskriti Vishwavidyalaya. Sanskriti UniversityMottoFor Excellence in LifeTypePrivate universityEstablished2016ChancellorDr.Sachin GuptaLocationChhata, Mathura, Uttar Pradesh, IndiaWebsitesanskriti.edu.in Sanskriti University is a private university located in Mathura, Uttar Pradesh, India. Academics Like all private unive...

UK chain of convenience stores This article has an unclear citation style. The references used may be made clearer with a different or consistent style of citation and footnoting. (April 2020) (Learn how and when to remove this template message) A Sainsbury’s Local store Sainsbury's Local (a trading name of Sainsbury's Supermarkets Ltd) is a chain of 770 convenience shops operated by the UK's second largest supermarket chain Sainsbury's.[1] History A store in York, North Yorkshire I...

United States historic placeRankin BuildingU.S. National Register of Historic PlacesU.S. Historic districtContributing property Contemporary view of the Rankin BuildingShow map of CaliforniaShow map of the United StatesLocation117 West Fourth Street at Sycamore, downtown Santa Ana, CaliforniaCoordinates33°44′54″N 117°52′06″W / 33.7482°N 117.8684°W / 33.7482; -117.8684Area0.2 acres (0.081 ha)Built1917Built byGeorge DrebleArchitectElwing and Tedford (San...

Danish journalist and schoolteacher, resistance fighter during World War II Hedda Lundh Hedda Lundh (1921–2012) was a Danish journalist and schoolteacher who, under the German occupation of Denmark in World War II, was a Danish resistance fighter. Based at the time in Aarhus, she is remembered as a railway saboteur, explosives expert and courier in the resistance movement.[1][2] Early life Born on 29 September 1921 in Korsør, Hedda Lundh was the daughter of the newspaper ed...

Indian actress Kirti KulhariKulhari in 2023Born (1985-05-30) 30 May 1985 (age 38)[1][2]Bombay, Maharashtra, IndiaOccupationActressYears active2009–presentSpouse Saahil Sehgal (m. 2016; sep. 2021) Kirti Kulhari (born 30 May 1985) is an Indian actress who works in Hindi-language films and series. She made her acting debut with the film Khichdi: The Movie in 2010 and then starred in Shaitan in 2011.[3] She th...