–ó–į–ī–į—á–į –ė–ĺ—Ā–ł—Ą–į –§–Ľ–į–≤–ł—Ź ‚ÄĒ –∑–į–ī–į—á–į, –≤—Ö–ĺ–ī—Ź—Č–į—Ź –≤ –ĺ–ī–Ĺ—É –ł–∑ —Ä–į–Ĺ–Ĺ–ł—Ö —Ä–į–Ī–ĺ—ā –Ņ–ĺ –∑–į–Ĺ–ł–ľ–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ (1612 –≥–ĺ–ī–į) –Ď–į—ą–Ķ –ī–Ķ –ú–Ķ–∑–ł—Ä–ł–į–ļ–į. –ó–į–ī–į—á–į –∑–į–ļ–Ľ—é—á–į–Ķ—ā—Ā—Ź –≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ: –Ņ–ĺ –ļ—Ä—É–≥—É —Ā—ā–ĺ–ł—ā 41 –≤–ĺ–ł–Ĺ, –Ĺ–į—á–ł–Ĺ–į—Ź —Ā –Ņ–Ķ—Ä–≤–ĺ–≥–ĺ –≤–ĺ–ł–Ĺ–į –ĺ–Ĺ–ł —É–Ī–ł–≤–į—é—ā –ļ–į–∂–ī–ĺ–≥–ĺ —ā—Ä–Ķ—ā—Ć–Ķ–≥–ĺ. –°–Ņ—Ä–į—ą–ł–≤–į–Ķ—ā—Ā—Ź, –≤ –ļ–į–ļ–ĺ–ľ –ľ–Ķ—Ā—ā–Ķ –Ĺ—É–∂–Ĺ–ĺ –≤—Ā—ā–į—ā—Ć, —á—ā–ĺ–Ī—č –ĺ—Ā—ā–į—ā—Ć—Ā—Ź –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł–ľ –≤—č–∂–ł–≤—ą–ł–ľ. –í –Ī–ĺ–Ľ–Ķ–Ķ –ĺ–Ī—Č–Ķ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–Ķ —É—á–į—Ā—ā–≤—É–Ķ—ā n –≤–ĺ–ł–Ĺ–ĺ–≤, –ļ–ĺ—ā–ĺ—Ä—č–Ķ —Ā—á–ł—ā–į—é—ā—Ā—Ź –Ņ–ĺ –ļ—Ä—É–≥—É, –ł —É–Ī–ł–≤–į—é—ā –ļ–į–∂–ī–ĺ–≥–ĺ m-–≥–ĺ.
–Ě–į–∑–≤–į–Ĺ–ł–Ķ –∑–į–ī–į—á–ł –≤–ĺ—Ā—Ö–ĺ–ī–ł—ā –ļ –ł—Ā—ā–ĺ—Ä–ł–ł, —Ā–Ľ—É—á–ł–≤—ą–Ķ–Ļ—Ā—Ź —Ā –ė–ĺ—Ā–ł—Ą–ĺ–ľ –§–Ľ–į–≤–ł–Ķ–ľ –≤–ĺ –≤—Ä–Ķ–ľ—Ź –ė—É–ī–Ķ–Ļ—Ā–ļ–ĺ–Ļ –≤–ĺ–Ļ–Ĺ—č.
–ė—Ā—ā–ĺ—Ä–ł—Ź
–≠—ā–į –∑–į–ī–į—á–į –ł–∑–≤–Ķ—Ā—ā–Ĺ–į —Ā 1612 –≥–ĺ–ī–į, –ļ–ĺ–≥–ī–į —Ą—Ä–į–Ĺ—Ü—É–∑—Ā–ļ–ł–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –Ď–į—ą–Ķ –ĺ–Ņ—É–Ī–Ľ–ł–ļ–ĺ–≤–į–Ľ —ć—ā—É –∑–į–ī–į—á—É –≤ —Ā–≤–ĺ—Ď–ľ —Ā–Ī–ĺ—Ä–Ĺ–ł–ļ–Ķ Problem es Plaisants. –°—é–∂–Ķ—ā –∑–į–ī–į—á–ł –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ –Ĺ–į –ł—Ā—ā–ĺ—Ä–ł–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ė–ĺ—Ā–ł—Ą–ĺ–ľ –§–Ľ–į–≤–ł–Ķ–ľ –≤ —Ā–≤–ĺ—Ď–ľ –ł—Ā—ā–ĺ—Ä–ł—á–Ķ—Ā–ļ–ĺ–ľ —ā—Ä—É–ī–Ķ ¬ę–ė—É–ī–Ķ–Ļ—Ā–ļ–į—Ź –≤–ĺ–Ļ–Ĺ–į¬Ľ.
–°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ —ć—ā–ĺ–Ļ –ł—Ā—ā–ĺ—Ä–ł–ł, –ė–ĺ—Ā–ł—Ą –§–Ľ–į–≤–ł–Ļ —Ā–ĺ —Ā–≤–ĺ–ł–ľ –ĺ—ā—Ä—Ź–ī–ĺ–ľ –ł–∑ —Ā–ĺ—Ä–ĺ–ļ–į —á–Ķ–Ľ–ĺ–≤–Ķ–ļ –Ņ–ĺ—Ā–Ľ–Ķ –Ņ–į–ī–Ķ–Ĺ–ł—Ź –ô–ĺ–ī—Ą–į—ā–į —Ā–ļ—Ä—č–Ľ—Ā—Ź –≤ –Ņ–Ķ—Č–Ķ—Ä–Ķ, –Ĺ–ĺ –Ī—č–Ľ –ĺ–Ī–Ĺ–į—Ä—É–∂–Ķ–Ĺ —Ä–ł–ľ–Ľ—Ź–Ĺ–į–ľ–ł.
–í—Ā–Ķ –≤ –ĺ—ā—Ä—Ź–ī–Ķ, –ļ—Ä–ĺ–ľ–Ķ –ė–ĺ—Ā–ł—Ą–į, –Ņ—Ä–Ķ–ī–Ņ–ĺ—á–Ľ–ł —Ā–ĺ–≤–Ķ—Ä—ą–ł—ā—Ć —Ā–į–ľ–ĺ—É–Ī–ł–Ļ—Ā—ā–≤–ĺ, –Ĺ–ĺ –Ĺ–Ķ —Ā–ī–į–≤–į—ā—Ć—Ā—Ź –≤ –Ņ–Ľ–Ķ–Ĺ.
–ė–ĺ—Ā–ł—Ą –Ņ—č—ā–į–Ľ—Ā—Ź –ĺ—ā–ļ–Ľ–ĺ–Ĺ–ł—ā—Ć —Ā–≤–ĺ–ł—Ö —ā–ĺ–≤–į—Ä–ł—Č–Ķ–Ļ –ĺ—ā —Ā–į–ľ–ĺ—É–Ī–ł–Ļ—Ā—ā–≤–į. –ě–ī–Ĺ–į–ļ–ĺ –ĺ–Ĺ–ł –ĺ–Ī–≤–ł–Ĺ—Ź–Ľ–ł –Ķ–≥–ĺ –≤ —ā—Ä—É—Ā–ĺ—Ā—ā–ł –ł —Ö–ĺ—ā–Ķ–Ľ–ł —É–Ī–ł—ā—Ć —Ā–≤–ĺ–Ķ–≥–ĺ –ļ–ĺ–ľ–į–Ĺ–ī–ł—Ä–į.
–Ē–į–Ľ–Ķ–Ķ –ė–ĺ—Ā–ł—Ą (–≥–ĺ–≤–ĺ—Ä—Ź –ĺ —Ā–Ķ–Ī–Ķ –≤ —ā—Ä–Ķ—ā—Ć–Ķ–ľ –Ľ–ł—Ü–Ķ) –Ņ–ł—ą–Ķ—ā:
–ė –≤ —ć—ā–ĺ–ľ —ā—Ź–∂—Ď–Ľ–ĺ–ľ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł –ė–ĺ—Ā–ł—Ą–į –Ĺ–Ķ –Ņ–ĺ–ļ–ł–Ĺ—É–Ľ–ĺ –Ķ–≥–ĺ –Ī–Ľ–į–≥–ĺ—Ä–į–∑—É–ľ–ł–Ķ: –≤ –Ĺ–į–ī–Ķ–∂–ī–Ķ –Ĺ–į –ľ–ł–Ľ–ĺ—Ā—ā—Ć –Ď–ĺ–∂–ł—é –ĺ–Ĺ —Ä–Ķ—ą–ł–Ľ —Ä–ł—Ā–ļ–Ĺ—É—ā—Ć —Ā–≤–ĺ–Ķ–Ļ –∂–ł–∑–Ĺ—Ć—é –ł —Ā–ļ–į–∑–į–Ľ: ¬ę–†–į–∑ —Ä–Ķ—ą–Ķ–Ĺ–ĺ —É–ľ–Ķ—Ä–Ķ—ā—Ć, —ā–į–ļ –ī–į–≤–į–Ļ—ā–Ķ –Ņ—Ä–Ķ–ī–ĺ—Ā—ā–į–≤–ł–ľ –∂—Ä–Ķ–Ī–ł—é —Ä–Ķ—ą–ł—ā—Ć, –ļ—ā–ĺ –ļ–ĺ–≥–ĺ –ī–ĺ–Ľ–∂–Ķ–Ĺ —É–Ī–ł–≤–į—ā—Ć. –Ę–ĺ—ā, –Ĺ–į –ļ–ĺ–≥–ĺ –Ņ–į–ī—Ď—ā –∂—Ä–Ķ–Ī–ł–Ļ, —É–ľ—Ä—Ď—ā –ĺ—ā —Ä—É–ļ –Ī–Ľ–ł–∂–į–Ļ—ą–Ķ–≥–ĺ –∑–į –Ĺ–ł–ľ, –ł —ā–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –ľ—č –≤—Ā–Ķ –Ņ–ĺ –ĺ—á–Ķ—Ä–Ķ–ī–ł –Ņ—Ä–ł–ľ–Ķ–ľ —Ā–ľ–Ķ—Ä—ā—Ć –ĺ–ī–ł–Ĺ –ĺ—ā –ī—Ä—É–≥–ĺ–≥–ĺ –ł –ł–∑–Ī–Ķ–≥–Ĺ–Ķ–ľ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł —Ā–į–ľ–ł —É–Ī–ł–≤–į—ā—Ć —Ā–Ķ–Ī—Ź; –Ī—É–ī–Ķ—ā, –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ, –Ĺ–Ķ—Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ, –Ķ—Ā–Ľ–ł –Ņ–ĺ—Ā–Ľ–Ķ —ā–ĺ–≥–ĺ, –ļ–į–ļ –ī—Ä—É–≥–ł–Ķ —É–∂–Ķ —É–ľ—Ä—É—ā, –ĺ–ī–ł–Ĺ —Ä–į–∑–ī—É–ľ–į–Ķ—ā –ł –ĺ—Ā—ā–į–Ĺ–Ķ—ā—Ā—Ź –≤ –∂–ł–≤—č—Ö¬Ľ. –≠—ā–ł–ľ –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ–ľ –ĺ–Ĺ –≤–Ĺ–ĺ–≤—Ć –≤–ĺ–∑–≤—Ä–į—ā–ł–Ľ —Ā–Ķ–Ī–Ķ –ł—Ö –ī–ĺ–≤–Ķ—Ä–ł–Ķ; —É–≥–ĺ–≤–ĺ—Ä–ł–≤ –ī—Ä—É–≥–ł—Ö, –ĺ–Ĺ —Ā–į–ľ —ā–į–ļ–∂–Ķ —É—á–į—Ā—ā–≤–ĺ–≤–į–Ľ —Ā –Ĺ–ł–ľ–ł –≤ –∂—Ä–Ķ–Ī–ł–ł. –ö–į–∂–ī—č–Ļ, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –Ņ–į–Ľ –∂—Ä–Ķ–Ī–ł–Ļ, –Ņ–ĺ –ĺ—á–Ķ—Ä–Ķ–ī–ł –ī–ĺ–Ī—Ä–ĺ–≤–ĺ–Ľ—Ć–Ĺ–ĺ –ī–į–Ľ —Ā–Ķ–Ī—Ź –∑–į–ļ–ĺ–Ľ–ĺ—ā—Ć –ī—Ä—É–≥–ĺ–ľ—É, –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į–≤—ą–Ķ–ľ—É –∑–į –Ĺ–ł–ľ —ā–ĺ–≤–į—Ä–ł—Č—É, —ā–į–ļ –ļ–į–ļ –≤—Ā–ļ–ĺ—Ä–Ķ –∑–į —ā–Ķ–ľ –ī–ĺ–Ľ–∂–Ķ–Ĺ –Ī—č–Ľ —É–ľ–Ķ—Ä–Ķ—ā—Ć —ā–į–ļ–∂–Ķ –ł –Ņ–ĺ–Ľ–ļ–ĺ–≤–ĺ–ī–Ķ—Ü, –į —Ā–ľ–Ķ—Ä—ā—Ć –≤–ľ–Ķ—Ā—ā–Ķ —Ā –ė–ĺ—Ā–ł—Ą–ĺ–ľ –ļ–į–∑–į–Ľ–į—Ā—Ć –ł–ľ –Ľ—É—á—ą–Ķ –∂–ł–∑–Ĺ–ł. –ü–ĺ —Ā—á–į—Ā—ā–Ľ–ł–≤–ĺ–Ļ –Ľ–ł —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ—Ā—ā–ł, –į –Ī—č—ā—Ć –ľ–ĺ–∂–Ķ—ā –Ņ–ĺ –Ī–ĺ–∂–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–ľ—É –Ņ—Ä–Ķ–ī–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é, –ĺ—Ā—ā–į–Ľ—Ā—Ź –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł–ľ –ł–ľ–Ķ–Ĺ–Ĺ–ĺ –ė–ĺ—Ā–ł—Ą –Ķ—Č—Ď —Ā –ĺ–ī–Ĺ–ł–ľ. –ź —ā–į–ļ –ļ–į–ļ –ĺ–Ĺ –Ĺ–Ķ —Ö–ĺ—ā–Ķ–Ľ –Ĺ–ł —Ā–į–ľ–ĺ–ľ—É –Ī—č—ā—Ć —É–Ī–ł—ā—č–ľ –Ņ–ĺ –∂—Ä–Ķ–Ī–ł—é, –Ĺ–ł –∑–į–Ņ—Ź—ā–Ĺ–į—ā—Ć —Ā–≤–ĺ–ł —Ä—É–ļ–ł –ļ—Ä–ĺ–≤—Ć—é —Ā–ĺ–ĺ—ā–Ķ—á–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ł–ļ–į, —ā–ĺ –ĺ–Ĺ —É–Ī–Ķ–ī–ł–Ľ –ł –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–Ķ–≥–ĺ —Ā–ī–į—ā—Ć—Ā—Ź —Ä–ł–ľ–Ľ—Ź–Ĺ–į–ľ –ł —Ā–ĺ—Ö—Ä–į–Ĺ–ł—ā—Ć —Ā–Ķ–Ī–Ķ –∂–ł–∑–Ĺ—Ć.–ė–ĺ—Ā–ł—Ą –§–Ľ–į–≤–ł–Ļ. –ė—É–ī–Ķ–Ļ—Ā–ļ–į—Ź –≤–ĺ–Ļ–Ĺ–į, –ļ–Ĺ–ł–≥–į 3, –≥–Ľ–į–≤–į 8, 7
–í –∑–į–ī–į—á–Ķ –Ď–į—ą–Ķ —Ā–ĺ–Ľ–ī–į—ā—č –Ĺ–Ķ –Ī—Ä–ĺ—Ā–į—é—ā –∂—Ä–Ķ–Ī–ł–Ļ, –į –≤—Ā—ā–į—é—ā –Ņ–ĺ –ļ—Ä—É–≥—É –ł —É–Ī–ł–≤–į—é—ā –ļ–į–∂–ī–ĺ–≥–ĺ —ā—Ä–Ķ—ā—Ć–Ķ–≥–ĺ. –í —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ —É –ė–ĺ—Ā–ł—Ą–į –Ņ–ĺ—Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –Ĺ–Ķ –Ņ–ĺ–Ľ–į–≥–į—ā—Ć—Ā—Ź –Ĺ–į –≤–ĺ–Ľ—é —Ā–Ľ—É—á–į—Ź, –į –≥–į—Ä–į–Ĺ—ā–ł—Ä–ĺ–≤–į–Ĺ–ĺ —Ā–Ņ–į—Ā—ā–ł—Ā—Ć. –Ď–į—ą–Ķ —Ā–Ņ—Ä–į—ą–ł–≤–į–Ķ—ā, –≥–ī–Ķ –Ĺ—É–∂–Ĺ–ĺ –≤—Ā—ā–į—ā—Ć –ė–ĺ—Ā–ł—Ą—É –ł –Ķ–≥–ĺ —ā–ĺ–≤–į—Ä–ł—Č—É, —á—ā–ĺ–Ī—č –ĺ—Ā—ā–į—ā—Ć—Ā—Ź –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł–ľ–ł, –Ĺ–į –ļ–ĺ–≥–ĺ –≤—č–Ņ–į–ī–Ķ—ā –∂—Ä–Ķ–Ī–ł–Ļ[1].
–ó–į–ī–į—á–į –≤–ī–ĺ—Ö–Ĺ–ĺ–≤–ł–Ľ–į –°—ā–į–Ĺ–ł—Ā–Ľ–į–≤–į –£–Ľ–į–ľ–į –Ĺ–į —Ā–ĺ–∑–ī–į–Ĺ–ł–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź —Ā—á–į—Ā—ā–Ľ–ł–≤–ĺ–≥–ĺ —á–ł—Ā–Ľ–į[1].
–Ě–į —Ä–Ķ—ą–Ķ–Ĺ–ł–ł –∑–į–ī–į—á–ł –ė–ĺ—Ā–ł—Ą–į –ī–Ľ—Ź  –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ —Ą–ĺ–ļ—É—Ā ¬ęLove Ritual¬Ľ[2], —Ā–ĺ–∑–ī–į–Ĺ–Ĺ—č–Ļ –ł—Ā–Ņ–į–Ĺ—Ā–ļ–ł–ľ —Ą–ĺ–ļ—É—Ā–Ĺ–ł–ļ–ĺ–ľ –í—É–ī–ł –ź—Ä–į–≥–ĺ–Ĺ–ĺ–ľ[–ł—Ā–Ņ.], –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ–ĺ–ļ–į–∑—č–≤–į—é—ā –ü–Ķ–Ĺ–Ĺ –ł –Ę–Ķ–Ľ–Ľ–Ķ—Ä[3].
–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ —Ą–ĺ–ļ—É—Ā ¬ęLove Ritual¬Ľ[2], —Ā–ĺ–∑–ī–į–Ĺ–Ĺ—č–Ļ –ł—Ā–Ņ–į–Ĺ—Ā–ļ–ł–ľ —Ą–ĺ–ļ—É—Ā–Ĺ–ł–ļ–ĺ–ľ –í—É–ī–ł –ź—Ä–į–≥–ĺ–Ĺ–ĺ–ľ[–ł—Ā–Ņ.], –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ–ĺ–ļ–į–∑—č–≤–į—é—ā –ü–Ķ–Ĺ–Ĺ –ł –Ę–Ķ–Ľ–Ľ–Ķ—Ä[3].
–†–Ķ–ļ—É—Ä—Ä–Ķ–Ĺ—ā–Ĺ—č–Ķ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź
–ē—Ā–Ľ–ł –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –∑–į–ī–į—á–ł –ī–Ľ—Ź –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ —á–ł—Ā–Ľ–į –≤–ĺ–ł–Ĺ–ĺ–≤, —ā–ĺ –Ķ–≥–ĺ –ľ–ĺ–∂–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –ī–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –∑–į–ī–į—á–ł —Ā –Ĺ–į –Ķ–ī–ł–Ĺ–ł—Ü—É –Ī–ĺ–Ľ—Ć—ą–ł–ľ —á–ł—Ā–Ľ–ĺ–ľ –≤–ĺ–ł–Ĺ–ĺ–≤.
–Ē–Ľ—Ź  –ł–ľ–Ķ–Ķ–ľ
–ł–ľ–Ķ–Ķ–ľ

–Ē–Ľ—Ź  –ł–ľ–Ķ–Ķ–ľ
–ł–ľ–Ķ–Ķ–ľ

–ě—á–Ķ–≤–ł–ī–Ĺ–ĺ –ī–Ľ—Ź –ĺ–Ī—Č–Ķ–≥–ĺ —Ā–Ľ—É—á–į—Ź –Ī—É–ī–Ķ–ľ –ł–ľ–Ķ—ā—Ć

–í–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ —Ä–Ķ–ļ—É—Ä—Ä–Ķ–Ĺ—ā–Ĺ—č—Ö —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ —Ā—Ö–ĺ–ī—Ź—ā—Ā—Ź –Ĺ–į–ľ–Ĺ–ĺ–≥–ĺ –Ī—č—Ā—ā—Ä–Ķ–Ķ —á–Ķ–ľ –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ—č–Ķ. –í–ĺ—ā –Ņ—Ä–ł–ľ–Ķ—Ä —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –∑–į–ī–į—á–ł –ī–Ľ—Ź  —Ā –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—á–Ķ—Ā–ļ–ł–ľ —á–ł—Ā–Ľ–ĺ–ľ —ą–į–≥–ĺ–≤ —Ä–Ķ–ļ—É—Ä—Ā–ł–ł:
—Ā –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—á–Ķ—Ā–ļ–ł–ľ —á–ł—Ā–Ľ–ĺ–ľ —ą–į–≥–ĺ–≤ —Ä–Ķ–ļ—É—Ä—Ā–ł–ł:

–†–Ķ—ą–Ķ–Ĺ–ł–Ķ –≤ –≤–ł–ī–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č
–ü—Ä–ł –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–ł –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—č–Ķ –≤—č—ą–Ķ —Ä–Ķ–ļ—É—Ä—Ä–Ķ–Ĺ—ā–Ĺ—č–Ķ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź –ī–į—é—ā –≤—č—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ—É—é —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć  –ł
–ł  —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ü–ĺ–Ľ—É—á–Ķ–Ĺ–ł–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –≤ –≤–ł–ī–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –ī–ĺ–Ľ–∂–Ĺ–ĺ –Ņ—Ä–ł–≤–ĺ–ī–ł—ā—Ć –ļ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į–ľ, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö –≤—č—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ–į—Ź —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–į ‚ÄĒ
—Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ü–ĺ–Ľ—É—á–Ķ–Ĺ–ł–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –≤ –≤–ł–ī–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –ī–ĺ–Ľ–∂–Ĺ–ĺ –Ņ—Ä–ł–≤–ĺ–ī–ł—ā—Ć –ļ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į–ľ, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö –≤—č—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ–į—Ź —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–į ‚ÄĒ  , —ā. –Ķ. –≤–ĺ–ĺ–Ī—Č–Ķ –Ĺ–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā
, —ā. –Ķ. –≤–ĺ–ĺ–Ī—Č–Ķ –Ĺ–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā  –ł
–ł  (–ī–Ľ–ł–Ĺ–į –∑–į–Ņ–ł—Ā–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź —á–ł—Ā–Ķ–Ľ –≤ —Ā–ł—Ā—ā–Ķ–ľ–Ķ —Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ĺ–Ķ —É—á–ł—ā—č–≤–į–Ķ—ā—Ā—Ź). –Ě–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–Ķ —ā–į–ļ–ł—Ö —Ą–ĺ—Ä–ľ—É–Ľ –ļ—Ä–į–Ļ–Ĺ–Ķ –∂–Ķ–Ľ–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ł –ī–Ľ—Ź –ī–į–Ĺ–Ĺ–ĺ–Ļ –∑–į–ī–į—á–ł.
(–ī–Ľ–ł–Ĺ–į –∑–į–Ņ–ł—Ā–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź —á–ł—Ā–Ķ–Ľ –≤ —Ā–ł—Ā—ā–Ķ–ľ–Ķ —Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ĺ–Ķ —É—á–ł—ā—č–≤–į–Ķ—ā—Ā—Ź). –Ě–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–Ķ —ā–į–ļ–ł—Ö —Ą–ĺ—Ä–ľ—É–Ľ –ļ—Ä–į–Ļ–Ĺ–Ķ –∂–Ķ–Ľ–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ł –ī–Ľ—Ź –ī–į–Ĺ–Ĺ–ĺ–Ļ –∑–į–ī–į—á–ł.
–Ē–Ľ—Ź  —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ņ—Ä–ĺ—Ā—ā–į—Ź —Ą–ĺ—Ä–ľ—É–Ľ–į:
—Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ņ—Ä–ĺ—Ā—ā–į—Ź —Ą–ĺ—Ä–ľ—É–Ľ–į:

–°–Ņ–ĺ—Ā–ĺ–Ī—č —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ņ–Ķ—Ä–Ķ–Ī–ĺ—Ä–ĺ–ľ
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ķ—Č—Ď –ī–≤–į —Ā–Ņ–ĺ—Ā–ĺ–Ī–į —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –∑–į–ī–į—á–ł, –Ĺ–Ķ –ĺ–Ņ–ł—Ä–į—é—Č–ł—Ö—Ā—Ź –Ĺ–į –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—É—é –≤—č—ą–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—É. –Ě–Ķ—Ā–ľ–ĺ—ā—Ä—Ź –Ĺ–į —ā–ĺ, —á—ā–ĺ –ĺ–Ĺ–ł —Ā–Ľ–ĺ–∂–Ĺ–Ķ–Ķ –ī–Ľ—Ź –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –≤ –Ņ–Ľ–į–Ĺ–Ķ –≤—č—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā–ł, –≤—Ā—Ď –∂–Ķ —ć—ā–ł –į–Ľ–≥–ĺ—Ä–ł—ā–ľ—č –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥–Ľ—Ź–ī–Ĺ—č.
–°–Ņ–ĺ—Ā–ĺ–Ī –Ņ–Ķ—Ä–≤—č–Ļ
–Ď—É–ī–Ķ–ľ —Ö—Ä–į–Ĺ–ł—ā—Ć –≤ –ľ–į—Ā—Ā–ł–≤–Ķ –ł–ľ–Ķ–Ĺ–į (—ā–ĺ –Ķ—Ā—ā—Ć –Ĺ–ĺ–ľ–Ķ—Ä–į) –≤—Ā–Ķ—Ö –∂–ł–≤—č—Ö –Ĺ–į —ā–Ķ–ļ—É—Č–ł–Ļ –ľ–ĺ–ľ–Ķ–Ĺ—ā –≤–ĺ–ł–Ĺ–ĺ–≤. –Ě–ĺ–ľ–Ķ—Ä–į –Ľ—é–ī–Ķ–Ļ –Ī—č–Ľ–ł –∑–į–Ņ–ł—Ā–į–Ĺ—č –≤ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ö –ľ–į—Ā—Ā–ł–≤–į —Ā 0 –Ņ–ĺ N ‚ÄĒ 1 (—ć—ā–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ –Ī—É–ī–Ķ—ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć—Ā—Ź –ī–Ľ—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –≤–∑—Ź—ā–ł—Ź –ĺ—Ā—ā–į—ā–ļ–į). –ö–ĺ–≥–ī–į –≤–ĺ–ł–Ĺ –Ī—É–ī–Ķ—ā —É–ľ–ł—Ä–į—ā—Ć, –Ī—É–ī–Ķ–ľ —É–ī–į–Ľ—Ź—ā—Ć –Ķ–≥–ĺ –ł–∑ –ľ–į—Ā—Ā–ł–≤–į, –ł —ā–Ķ—Ö, –ļ—ā–ĺ —Ā—ā–ĺ—Ź–Ľ –∑–į –Ĺ–ł–ľ, ¬ę—Ā–ī–≤–ł–≥–į—ā—ƬĽ –Ĺ–į –ĺ–ī–ł–Ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā –≤–Ľ–Ķ–≤–ĺ.
–ó–į–ľ–Ķ—ā–ł–ľ, —á—ā–ĺ –Ķ—Ā–Ľ–ł –ľ—č —É–∂–Ķ —É–Ī–ł–Ľ–ł L —á–Ķ–Ľ–ĺ–≤–Ķ–ļ, —ā–ĺ –≤ –∂–ł–≤—č—Ö –ĺ—Ā—ā–į–Ľ–ĺ—Ā—Ć M = N ‚ÄĒ L. –ü—É—Ā—ā—Ć –ľ—č —ā–ĺ–Ľ—Ć–ļ–ĺ —á—ā–ĺ (–Ĺ–į L-–ĺ–ľ —ą–į–≥–Ķ) —É–Ī–ł–Ľ–ł —á–Ķ–Ľ–ĺ–≤–Ķ–ļ–į, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ī—č–Ľ –∑–į–Ņ–ł—Ā–į–Ĺ –≤ –Ĺ–į—ą–Ķ–ľ –ľ–į—Ā—Ā–ł–≤–Ķ –≤ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–Ķ —Ā –Ĺ–ĺ–ľ–Ķ—Ä–ĺ–ľ j (–ł —Ā–ī–≤–ł–Ĺ—É–Ľ–ł –Ľ—é–ī–Ķ–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ī—č–Ľ–ł –∑–į–Ņ–ł—Ā–į–Ĺ—č –≤ –ľ–į—Ā—Ā–ł–≤–Ķ –≤ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ö —Ā j + 1 –Ņ–ĺ M –Ĺ–į –ĺ–ī–ł–Ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā –≤–Ľ–Ķ–≤–ĺ). –Ę–ĺ–≥–ī–į —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –Ĺ—É–∂–Ĺ–ĺ —É–Ī–ł–≤–į—ā—Ć —á–Ķ–Ľ–ĺ–≤–Ķ–ļ–į, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –∑–į–Ņ–ł—Ā–į–Ĺ –≤ —ć—ā–ĺ–ľ –ľ–į—Ā—Ā–ł–≤–Ķ –≤ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–Ķ —Ā –Ĺ–ĺ–ľ–Ķ—Ä–ĺ–ľ (j + k ‚ÄĒ 1) % M
–°–Ņ–ĺ—Ā–ĺ–Ī –≤—ā–ĺ—Ä–ĺ–Ļ
–ó–į–≤–Ķ–ī–Ķ–ľ –ľ–į—Ā—Ā–ł–≤, –≥–ī–Ķ –Ī—É–ī–Ķ–ľ –Ņ–ĺ–ľ–Ķ—á–į—ā—Ć –ľ—Ď—Ä—ā–≤—č—Ö –≤–ĺ–ł–Ĺ–ĺ–≤ (—ā–ĺ –Ķ—Ā—ā—Ć –≤ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–Ķ i —Ö—Ä–į–Ĺ–ł—ā—Ā—Ź, –∂–ł–≤ –≤–ĺ–ł–Ĺ i, –ł–Ľ–ł —É–∂–Ķ –Ĺ–Ķ—ā). –ü—É—Ā—ā—Ć —É –Ĺ–į—Ā –Ĺ–į —ā–Ķ–ļ—É—Č–Ķ–ľ —ą–į–≥–Ķ M –∂–ł–≤—č—Ö –Ľ—é–ī–Ķ–Ļ, –į –Ĺ–į –Ņ—Ä–Ķ–ī—č–ī—É—Č–Ķ–ľ —ą–į–≥–Ķ —É–ľ–Ķ—Ä –≤–ĺ–ł–Ĺ j. –ß—ā–ĺ–Ī—č –Ĺ–į–Ļ—ā–ł —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–≥–ĺ, –Ī—É–ī–Ķ–ľ –Ī–Ķ–∂–į—ā—Ć –Ņ–ĺ –ľ–į—Ā—Ā–ł–≤—É, –ĺ—ā—Ā—á–ł—ā—č–≤–į—Ź –∂–ł–≤—č—Ö –ł –Ņ—Ä–ĺ–Ņ—É—Ā–ļ–į—Ź –ľ—Ď—Ä—ā–≤—č—Ö. –Ę–ĺ—ā —á–Ķ–Ľ–ĺ–≤–Ķ–ļ, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ –ľ—č –Ĺ–į—Ā—á–ł—ā–į–Ķ–ľ k % M, –ł –ī–ĺ–Ľ–∂–Ķ–Ĺ —É–ľ–Ķ—Ä–Ķ—ā—Ć —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ. –ß–Ķ—Ä–Ķ–∑ N ‚ÄĒ 1 —ą–į–≥–ĺ–≤ –ĺ—Ā—ā–į–Ĺ–Ķ—ā—Ā—Ź –ĺ–ī–ł–Ĺ —á–Ķ–Ľ–ĺ–≤–Ķ–ļ.
–†–Ķ–ļ—É—Ä—Ā–ł–≤–Ĺ–ĺ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ
–ü—Ä–ĺ—Ā—ā–Ķ–Ļ—ą–Ķ–Ķ –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –Ī—É–ī–Ķ—ā —Ä–į–Ī–ĺ—ā–į—ā—Ć –∑–į  . –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ī–Ķ—Ä–Ķ–≤–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤, –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ—Ā—ā–ł –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –∑–į
. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ī–Ķ—Ä–Ķ–≤–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤, –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ—Ā—ā–ł –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –∑–į  .
–ě–ī–Ĺ–į–ļ–ĺ –Ņ–ĺ–Ņ—č—ā–į–Ķ–ľ—Ā—Ź –Ĺ–į–Ļ—ā–ł –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć, –≤—č—Ä–į–∂–į—é—Č—É—é –ĺ—ā–≤–Ķ—ā –ī–Ľ—Ź –∑–į–ī–į—á–ł (N,K) —á–Ķ—Ä–Ķ–∑ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ņ—Ä–Ķ–ī—č–ī—É—Č–ł—Ö –∑–į–ī–į—á.
–° –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ —ā–į–Ī–Ľ–ł—Ü—É –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ, —Ā–ļ–į–∂–Ķ–ľ, –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—É—é –Ĺ–ł–∂–Ķ.
.
–ě–ī–Ĺ–į–ļ–ĺ –Ņ–ĺ–Ņ—č—ā–į–Ķ–ľ—Ā—Ź –Ĺ–į–Ļ—ā–ł –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć, –≤—č—Ä–į–∂–į—é—Č—É—é –ĺ—ā–≤–Ķ—ā –ī–Ľ—Ź –∑–į–ī–į—á–ł (N,K) —á–Ķ—Ä–Ķ–∑ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ņ—Ä–Ķ–ī—č–ī—É—Č–ł—Ö –∑–į–ī–į—á.
–° –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ —ā–į–Ī–Ľ–ł—Ü—É –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ, —Ā–ļ–į–∂–Ķ–ľ, –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—É—é –Ĺ–ł–∂–Ķ.
–Ę–į–Ī–Ľ–ł—Ü–į
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10
|
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1
|
| 2 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1
|
| 3 |
3 |
3 |
2 |
2 |
1 |
1 |
3 |
3 |
2 |
2
|
| 4 |
4 |
1 |
1 |
2 |
2 |
3 |
2 |
3 |
3 |
4
|
| 5 |
5 |
3 |
4 |
1 |
2 |
4 |
4 |
1 |
2 |
4
|
| 6 |
6 |
5 |
1 |
5 |
1 |
4 |
5 |
3 |
5 |
2
|
| 7 |
7 |
7 |
4 |
2 |
6 |
3 |
5 |
4 |
7 |
5
|
| 8 |
8 |
1 |
7 |
6 |
3 |
1 |
4 |
4 |
8 |
7
|
| 9 |
9 |
3 |
1 |
1 |
8 |
7 |
2 |
3 |
8 |
8
|
| 10 |
10 |
5 |
4 |
5 |
3 |
3 |
9 |
1 |
7 |
8
|
joseph (n, k) = ( joseph (n-1, k) + k - 1 ) % n + 1;
joseph (1, k) = 1
(–∑–ī–Ķ—Ā—Ć –ł–Ĺ–ī–Ķ–ļ—Ā–į—Ü–ł—Ź —Ā –Ķ–ī–ł–Ĺ–ł—Ü—č –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –Ņ–ĺ—Ä—ā–ł—ā —ć–Ľ–Ķ–≥–į–Ĺ—ā–Ĺ–ĺ—Ā—ā—Ć —Ą–ĺ—Ä–ľ—É–Ľ—č)
–ė—ā–į–ļ, –ľ—č –Ĺ–į—ą–Ľ–ł —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –∑–į–ī–į—á–ł –ė–ĺ—Ā–ł—Ą–į –§–Ľ–į–≤–ł—Ź, —Ä–į–Ī–ĺ—ā–į—é—Č–Ķ–Ķ –∑–į  –ł—ā–Ķ—Ä–į—Ü–ł–Ļ.
–ł—ā–Ķ—Ä–į—Ü–ł–Ļ.
–ü—Ä–ł–ľ–Ķ—Ä
–° —Ü–Ķ–Ľ—Ć—é –Ņ–ĺ–ī—Ä–ĺ–Ī–Ĺ–ĺ–≥–ĺ –ĺ–Ī—ä—Ź—Ā–Ĺ–Ķ–Ĺ–ł—Ź –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č—Ö —Ā–ł—ā—É–į—Ü–ł–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–ĺ–≥—É—ā –≤–ĺ–∑–Ĺ–ł–ļ–Ĺ—É—ā—Ć –≤ —Ö–ĺ–ī–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź, —É–Ņ—Ä–ĺ—Ā—ā–ł–ľ –ł—Ā—Ö–ĺ–ī–Ĺ—É—é –∑–į–ī–į—á—É –ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —Ā–Ľ—É—á–į–Ļ ‚ĄĖ 1, –Ņ—Ä–ł—á–Ķ–ľ, —É–ľ–Ķ–Ĺ—Ć—ą–ł–ľ –ļ—Ä—É–≥ —Ā–ĺ–Ľ–ī–į—ā —Ā —Ā–ĺ—Ä–ĺ–ļ–į –ĺ–ī–Ĺ–ĺ–≥–ĺ (—Ā–ĺ—Ä–ĺ–ļ —Ā–ĺ–Ľ–ī–į—ā –ł –ė–ĺ—Ā–ł—Ą) –ī–ĺ –ī–Ķ—Ā—Ź—ā–ł –ł –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł–ľ, —á—ā–ĺ –≤–ľ–Ķ—Ā—ā–ĺ –ļ–į–∂–ī–ĺ–≥–ĺ —ā—Ä–Ķ—ā—Ć–Ķ–≥–ĺ —Ā–ĺ–Ľ–ī–į—ā–į –ī–ĺ–Ľ–∂–Ķ–Ĺ —É–ľ–Ķ—Ä–Ķ—ā—Ć –ļ–į–∂–ī—č–Ļ –≤—ā–ĺ—Ä–ĺ–Ļ. –í —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–Ķ –Ī—É–ī–Ķ–ľ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ—Ä—É–≥ —Ā–ĺ–Ľ–ī–į—ā, –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ–Ĺ—č–Ļ –Ĺ–į —Ä–ł—Ā 1.
|
| –†–ł—Ā 1. –ö—Ä—É–≥ –ł–∑ 10 —Ā–ĺ–Ľ–ī–į—ā, –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ
|
| –ī–ĺ–Ľ–∂–Ķ–Ĺ ¬ę—É–ľ–Ķ—Ä–Ķ—ā—ƬĽ –ļ–į–∂–ī—č–Ļ –≤—ā–ĺ—Ä–ĺ–Ļ
|
–ē—Ā–Ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ć –ĺ—ā—Ā—á–Ķ—ā –ĺ—ā 1-–≥–ĺ —Ā–ĺ–Ľ–ī–į—ā–į –≤ –ļ—Ä—É–≥–Ķ, —ā–ĺ –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ —É–ī–į–Ľ–Ķ–Ĺ–ł—Ź –Ī—É–ī–Ķ—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ:
2, 4, 6, 8, 10, 3, 7, 1, 9. –°–ĺ–Ľ–ī–į—ā –Ņ–ĺ–ī –Ĺ–ĺ–ľ–Ķ—Ä–ĺ–ľ 5 ‚ÄĒ –≤ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–ľ –ł—ā–ĺ–≥–Ķ –ĺ—Ā—ā–į–Ĺ–Ķ—ā—Ā—Ź –≤ –∂–ł–≤—č—Ö.
–≠—ā–į–Ņ—č ¬ę—É–Ĺ–ł—á—ā–ĺ–∂–Ķ–Ĺ–ł—Ź¬Ľ —Ā–ĺ–Ľ–ī–į—ā –ł–∑ –ļ—Ä—É–≥–į –≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ—č –Ĺ–į —Ä–ł—Ā. 2‚ÄĒ4.
|

|
|
| –†–ł—Ā 2. 1-–Ļ —ć—ā–į–Ņ —É–ī–į–Ľ–Ķ–Ĺ–ł—Ź
|
–†–ł—Ā 3. 2-–Ļ —ć—ā–į–Ņ —É–ī–į–Ľ–Ķ–Ĺ–ł—Ź
|
–†–ł—Ā 4. 3-–Ļ —ć—ā–į–Ņ —É–ī–į–Ľ–Ķ–Ĺ–ł—Ź
|
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ—É—é —Ā–ł—ā—É–į—Ü–ł—é –ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–ľ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā—č, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –Ņ—Ä–Ķ–ī–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ—č–Ķ —É—Ā–Ľ–ĺ–≤–ł—Ź. –ó–į–ī–į—á–į —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ —ā–ĺ–ľ, —á—ā–ĺ–Ī—č —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ľ–Ķ–∂–ī—É –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–į–ľ–ł k, n (–≥–ī–Ķ n ‚ÄĒ —ć—ā–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –Ľ—é–ī–Ķ–Ļ –≤ –ļ—Ä—É–≥–Ķ, k ‚ÄĒ —Ā–Ľ—É–∂–ł—ā –ī–Ľ—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –ļ–į–∂–ī–ĺ–≥–ĺ k-–≥–ĺ —Ā–ĺ–Ľ–ī–į—ā–į –ī–Ľ—Ź ¬ę–ł—Ā–ļ–Ľ—é—á–Ķ–Ĺ–ł—Ź¬Ľ –ł–∑ –ļ—Ä—É–≥–į), –ł —Ä–Ķ—ą–ł—ā—Ć –∑–į–ī–į—á—É –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā —ā–ĺ–≥–ĺ, —Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ —Ā–ĺ–Ľ–ī–į—ā —Ā—ā–ĺ—Ź—ā –≤ –ļ—Ä—É–≥–Ķ.
–ü–ĺ–Ņ—Ä–ĺ–Ī—É–Ķ–ľ –≤—č–≤–Ķ—Ā—ā–ł –ĺ–Ī—Č–ł–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –ī–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –∑–į–ī–į—á–ł —Ā –Ľ—é–Ī—č–ľ–ł –≤—Ö–ĺ–ī–Ĺ—č–ľ–ł –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–į–ľ–ł (–Ĺ–į –≤—Ö–ĺ–ī –Ņ–ĺ–ī–į—é—ā—Ā—Ź –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź k –ł n). –Ē–Ľ—Ź —ć—ā–ĺ–≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ–ľ —Ą—É–Ĺ–ļ—Ü–ł—é F(n), –≥–ī–Ķ F(n) ‚ÄĒ –≤–ĺ–∑–≤—Ä–į—Č–į–Ķ—ā –Ĺ–ĺ–ľ–Ķ—Ä –Ņ–ĺ–Ī–Ķ–ī–ł—ā–Ķ–Ľ—Ź.
–°—Ä–į–∑—É –≤–ĺ–∑–Ĺ–ł–ļ–į–Ķ—ā –Ņ–Ķ—Ä–≤–ĺ–Ķ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ, —á—ā–ĺ F(n) –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –≤ –Ņ—Ä–Ķ–ī–Ķ–Ľ–į—Ö F(n) = n / 2, —á—ā–ĺ –≤–Ķ—Ä–Ĺ–ĺ –Ņ—Ä–ł n = 10 –ł–Ľ–ł n = 2. –ě–ī–Ĺ–į–ļ–ĺ –Ņ—Ä–ł n = 4 F(4) = 1, —á—ā–ĺ –ī–ĺ–ļ–į–∑—č–≤–į–Ķ—ā –Ĺ–Ķ–Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć —Ä–į—Ā—Ā—É–∂–ī–Ķ–Ĺ–ł–Ļ.
–°–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ –∑–į–ľ–Ķ—á–į–Ĺ–ł–Ķ –ł–∑ —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ –≤—č—ą–Ķ —Ā–ł—ā—É–į—Ü–ł–ł: –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ—č–Ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā ‚ÄĒ –Ĺ–Ķ—á—Ď—ā–Ĺ—č–Ļ –Ĺ–ĺ–ľ–Ķ—Ä, –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź n, —ā–į–ļ –Ņ—Ä–ĺ–ł–∑–ĺ—ą–Ľ–ĺ –≤—Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ —ā–ĺ–≥–ĺ, —á—ā–ĺ –≤ —Ö–ĺ–ī–Ķ 1-–≥–ĺ —ć—ā–į–Ņ–į ‚ÄĒ –Ī—č–Ľ–ł —É–Ī—Ä–į–Ĺ—č –≤—Ā–Ķ —á–Ķ—ā–Ĺ—č–Ķ –Ĺ–ĺ–ľ–Ķ—Ä–į. –Ę–į–ļ–∂–Ķ —Ā–Ľ–Ķ–ī—É–Ķ—ā —É—á–Ķ—Ā—ā—Ć —ā–ĺ—ā —Ą–į–ļ—ā, —á—ā–ĺ –Ņ—Ä–ł n = 1 F(1) = 1.
–ü—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł–≤, —á—ā–ĺ –Ĺ–į –≤—Ö–ĺ–ī–Ķ —Ā–ĺ–Ľ–ī–į—ā = 2n. –Ę–ĺ, —á—ā–ĺ –ĺ—Ā—ā–į—Ď—ā—Ā—Ź –Ņ–ĺ—Ā–Ľ–Ķ 1-–≥–ĺ —ć—ā–į–Ņ–į –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –Ĺ–į —Ä–ł—Ā. 5.

|
| –†–ł—Ā. 5 ‚ÄĒ 1-–Ļ —ć—ā–į–Ņ –Ņ—Ä–ł –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ —Ā–ĺ–Ľ–ī–į—ā –≤ –ļ—Ä—É–≥–Ķ 2n
|
–Ě–į–Ī–Ľ—é–ī–į–Ķ—ā—Ā—Ź –į–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–į—Ź —Ā–ł—ā—É–į—Ü–ł—Ź –ł –Ņ—Ä–ł 2n‚ąí1 —Ā–ĺ–Ľ–ī–į—ā–į—Ö –Ĺ–į –≤—Ö–ĺ–ī–Ķ (—Ä–ł—Ā. 6). –ě–ī–Ĺ–į–ļ–ĺ –≤–≤–ĺ–ī–ł—ā—Ā—Ź –Ņ–ĺ–Ņ—Ä–į–≤–ļ–į ‚ÄĒ —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ķ–ī–ł–Ĺ–ł—Ü—É –ł —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ F(n) –≤ 2 —Ä–į–∑–į.
|
| –†–ł—Ā. 6. —Ā–ĺ–Ľ–ī–į—ā –≤ –ļ—Ä—É–≥–Ķ 2n-1
|
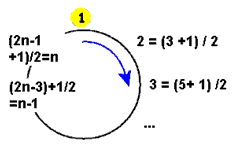
–ė–∑ —á–Ķ–≥–ĺ –ľ–ĺ–∂–Ĺ–ĺ –≤—č–≤–Ķ—Ā—ā–ł —Ą–ĺ—Ä–ľ—É–Ľ—É F(2n) = 2 F(n) ‚ąí 1 (–ī–Ľ—Ź –≤—Ā–Ķ—Ö n > 1).
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —Ā–Ľ—É—á–į–Ļ ‚ĄĖ 2, –Ņ—Ä–ł–Ĺ—Ź–≤ –≤–ĺ –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ —ā–ĺ—ā —Ą–į–ļ—ā, —á—ā–ĺ –Ĺ–į –≤—Ö–ĺ–ī –Ņ–ĺ–ī–į—é—ā—Ā—Ź 2n + 1 —á–ł—Ā–Ľ–ĺ —Ā–ĺ–Ľ–ī–į—ā (—ā–ĺ –Ķ—Ā—ā—Ć –Ĺ–Ķ—á—Ď—ā–Ĺ–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —Ā–ĺ–Ľ–ī–į—ā). –ü–ĺ—Ā–Ľ–Ķ –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł—Ź 1-–≥–ĺ —ć—ā–į–Ņ–į ¬ę–ł—Ā–ļ–Ľ—é—á–Ķ–Ĺ–ł—Ź¬Ľ —Ā–ĺ–Ľ–ī–į—ā –ł–∑ –ļ—Ä—É–≥–į –Ņ–ĺ–Ľ—É—á–ł—ā—Ā—Ź –Ĺ–Ķ—á—ā–ĺ, –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ķ –Ĺ–į —Ä–ł—Ā. 7.
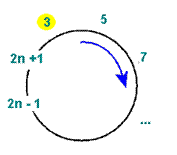
|
| –†–ł—Ā. 7 ‚ÄĒ 1-–Ļ —ć—ā–į–Ņ –Ņ—Ä–ł –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ —Ā–ĺ–Ľ–ī–į—ā –≤ –ļ—Ä—É–≥–Ķ 2n + 1
|
–ė–∑ —á–Ķ–≥–ĺ –ľ–ĺ–∂–Ĺ–ĺ –≤—č–≤–Ķ—Ā—ā–ł —Ą–ĺ—Ä–ľ—É–Ľ—É F(2n +1) = 2 F(n) + 1 (–ī–Ľ—Ź –≤—Ā–Ķ—Ö n > 1).
–°–≤–Ķ–ī—Ď–ľ –≤—Ā–Ķ —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–Ĺ—č–Ķ —Ā–ł—ā—É–į—Ü–ł–ł –ł –∑–į–Ņ–ł—ą–Ķ–ľ –≤—Ā–Ķ —Ā–Ľ—É—á–į–ł –≤ –≤–ł–ī–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č, –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź—é—Č–Ķ–Ļ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł F(n) –ī–Ľ—Ź –Ľ—é–Ī—č—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ n:
–í—č–≤–Ķ–ī–Ķ–Ĺ–Ĺ—č–Ķ –≤—č—ą–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ—č –ł –ī–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ļ –∑–į–ī–į—á–ł –ė–ĺ—Ā–ł—Ą–į –§–Ľ–į–≤–ł—Ź.
–ź –ł–ľ–Ķ–Ĺ–Ĺ–ĺ:
F(2m + k) = 2k + 1 –ī–Ľ—Ź –Ľ—é–Ī—č—Ö m –ł k.
–ü—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –ī–Ľ—Ź —Ā–Ľ—É—á–į—Ź —É–Ī–ł–Ļ—Ā—ā–≤–į –ļ–į–∂–ī–ĺ–≥–ĺ 2-–≥–ĺ —á–Ķ—Ä–Ķ–∑ –ī–≤–ĺ–ł—á–Ĺ—É—é –∑–į–Ņ–ł—Ā—Ć
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –ī–≤–ĺ–ł—á–Ĺ—č–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź–ľ –≤–Ķ–Ľ–ł—á–ł–Ĺ n –ł F(n):
 ,
–≥–ī–Ķ –ļ–į–∂–ī–ĺ–Ķ
,
–≥–ī–Ķ –ļ–į–∂–ī–ĺ–Ķ  —Ä–į–≤–Ĺ–ĺ 0 –ł–Ľ–ł 1, –Ņ—Ä–ł—á–Ķ–ľ —Ā—ā–į—Ä—ą–ł–Ļ –Ī–ł—ā
—Ä–į–≤–Ĺ–ĺ 0 –ł–Ľ–ł 1, –Ņ—Ä–ł—á–Ķ–ľ —Ā—ā–į—Ä—ą–ł–Ļ –Ī–ł—ā  —Ä–į–≤–Ķ–Ĺ 1. –í—Ā–Ņ–ĺ–ľ–ł–Ĺ–į—Ź, —á—ā–ĺ
—Ä–į–≤–Ķ–Ĺ 1. –í—Ā–Ņ–ĺ–ľ–ł–Ĺ–į—Ź, —á—ā–ĺ  , –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ:
, –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ:


(—ā–į–ļ –ļ–į–ļ  )
)

(—ā–į–ļ –ļ–į–ļ  )
)


(—ā–į–ļ –ļ–į–ļ  –ł
–ł  )
)
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ľ—č –Ņ–ĺ–Ľ—É—á–ł–Ľ–ł, —á—ā–ĺ
 ,
,
—ā–ĺ –Ķ—Ā—ā—Ć F(n) –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –Ņ—É—ā—Ď–ľ —Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ā–ī–≤–ł–≥–į –ī–≤–ĺ–ł—á–Ĺ–ĺ–≥–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź n –≤–Ľ–Ķ–≤–ĺ –Ĺ–į –ĺ–ī–Ĺ—É –Ņ–ĺ–∑–ł—Ü–ł—é.
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į