–£ —Н—В–Њ–≥–Њ —В–µ—А–Љ–Є–љ–∞ —Б—Г—Й–µ—Б—В–≤—Г—О—В –Є –і—А—Г–≥–Є–µ –Ј–љ–∞—З–µ–љ–Є—П, —Б–Љ.
–С–µ–љ—В.
![]() –С–Є–љ–∞—А–љ—Л–µ –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–Є —Б —А–∞—Б—Б—В–Њ—П–љ–Є–µ–Љ –•—Н–Љ–Љ–Є–љ–≥–∞, —А–∞–≤–љ—Л–Љ 1 –Є –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В—М—О
–С–Є–љ–∞—А–љ—Л–µ –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–Є —Б —А–∞—Б—Б—В–Њ—П–љ–Є–µ–Љ –•—Н–Љ–Љ–Є–љ–≥–∞, —А–∞–≤–љ—Л–Љ 1 –Є –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В—М—О 
 –Э–µ–ї–Є–љ–µ–є–љ–Њ—Б—В—М –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–Є
–Э–µ–ї–Є–љ–µ–є–љ–Њ—Б—В—М –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–Є  —А–∞–≤–љ–∞
—А–∞–≤–љ–∞ 
–С–µ–љ—В-—Д—Г–љ–Ї—Ж–Є—П (–Њ—В –∞–љ–≥–ї. bent вАФ ¬Ђ–Є–Ј–Њ–≥–љ—Г—В—Л–є, –љ–∞–Ї–ї–Њ–љ—С–љ–љ—Л–є¬ї[1], [2]) вАФ –±—Г–ї–µ–≤–∞ —Д—Г–љ–Ї—Ж–Є—П —Б —З—С—В–љ—Л–Љ —З–Є—Б–ї–Њ–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е, –і–ї—П –Ї–Њ—В–Њ—А–Њ–є —А–∞—Б—Б—В–Њ—П–љ–Є–µ –•—Н–Љ–Љ–Є–љ–≥–∞ –Њ—В –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –∞—Д—Д–Є–љ–љ—Л—Е –±—Г–ї–µ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є–є —Б —В–µ–Љ –ґ–µ —З–Є—Б–ї–Њ–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ. –С–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–Є –≤ —Н—В–Њ–Љ —Б–Љ—Л—Б–ї–µ –Њ–±–ї–∞–і–∞—О—В –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–є —Б—В–µ–њ–µ–љ—М—О –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В–Є —Б—А–µ–і–Є –≤—Б–µ—Е —Д—Г–љ–Ї—Ж–Є–є —Б –і–∞–љ–љ—Л–Љ —З–Є—Б–ї–Њ–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е –Є –±–ї–∞–≥–Њ–і–∞—А—П —Н—В–Њ–Љ—Г —И–Є—А–Њ–Ї–Њ –њ—А–Є–Љ–µ–љ—П—О—В—Б—П –≤ –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є–Є –і–ї—П —Б–Њ–Ј–і–∞–љ–Є—П —И–Є—Д—А–Њ–≤, –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ —Г—Б—В–Њ–є—З–Є–≤—Л—Е –Ї –Љ–µ—В–Њ–і–∞–Љ –ї–Є–љ–µ–є–љ–Њ–≥–Њ –Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ –Ї—А–Є–њ—В–Њ–∞–љ–∞–ї–Є–Ј–∞[1].
–Т —А—Г—Б—Б–Ї–Њ—П–Ј—Л—З–љ–Њ–є –ї–Є—В–µ—А–∞—В—Г—А–µ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –±–ї–Є–Ј–Ї–Є–є –њ–Њ —Б–Љ—Л—Б–ї—Г —В–µ—А–Љ–Є–љ ¬Ђ–Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ –љ–µ–ї–Є–љ–µ–є–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П¬ї, —З–Є—Б–ї–Њ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е —В–∞–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –љ–µ –Њ–≥—А–∞–љ–Є—З–Є–≤–∞–µ—В—Б—П —З—С—В–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є. –Ь–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ –љ–µ–ї–Є–љ–µ–є–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П —Б —З—С—В–љ—Л–Љ —З–Є—Б–ї–Њ–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е —П–≤–ї—П–µ—В—Б—П –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–µ–є [1].
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є—П
–†–∞—Б—Б—В–Њ—П–љ–Є–µ –•—Н–Љ–Љ–Є–љ–≥–∞ –і–ї—П –і–≤—Г—Е –±—Г–ї–µ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є–є n –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е вАФ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —А–∞–Ј–ї–Є—З–Є–є –≤ –Ј–љ–∞—З–µ–љ–Є—П—Е —Н—В–Є—Е —Д—Г–љ–Ї—Ж–Є–є –љ–∞ –њ–Њ–ї–љ–Њ–Љ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ –Є–Ј 2n –љ–∞–±–Њ—А–Њ–≤ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е.
–Р—Д—Д–Є–љ–љ–∞—П (–ї–Є–љ–µ–є–љ–∞—П) –±—Г–ї–µ–≤–∞ —Д—Г–љ–Ї—Ж–Є—П вАФ –±—Г–ї–µ–≤–∞ —Д—Г–љ–Ї—Ж–Є—П, –њ–Њ–ї–Є–љ–Њ–Љ –Ц–µ–≥–∞–ї–Ї–Є–љ–∞ –Ї–Њ—В–Њ—А–Њ–є –љ–µ –Є–Љ–µ–µ—В –љ–µ–ї–Є–љ–µ–є–љ—Л—Е —З–ї–µ–љ–Њ–≤, —В–Њ –µ—Б—В—М —З–ї–µ–љ–Њ–≤, –њ—А–µ–і—Б—В–∞–≤–ї—П—О—Й–Є—Е —Б–Њ–±–Њ–є –Ї–Њ–љ—К—О–љ–Ї—Ж–Є—О –љ–µ—Б–Ї–Њ–ї—М–Ї–Є—Е –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е.
–°—В–µ–њ–µ–љ—М –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В–Є –±—Г–ї–µ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є deg(f) вАФ —З–Є—Б–ї–Њ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е –≤ —Б–∞–Љ–Њ–Љ –і–ї–Є–љ–љ–Њ–Љ —Б–ї–∞–≥–∞–µ–Љ–Њ–Љ –µ—С –њ–Њ–ї–Є–љ–Њ–Љ–∞ –Ц–µ–≥–∞–ї–Ї–Є–љ–∞.
–Э–µ–ї–Є–љ–µ–є–љ–Њ—Б—В—М –±—Г–ї–µ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є N(f) вАФ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –•—Н–Љ–Љ–Є–љ–≥–∞ –Њ—В –і–∞–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –і–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –≤—Б–µ—Е –∞—Д—Д–Є–љ–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є.
–Ш—Б—В–Њ—А–Є—П
–С–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–Є –±—Л–ї–Є –≤–≤–µ–і–µ–љ—Л –≤ 1960-—Е –≥–Њ–і–∞—Е –Ю—Б–Ї–∞—А–Њ–Љ –†–Њ—В—Е–∞—Г–Ј–Њ–Љ (1927вАФ2003), –Ї–Њ—В–Њ—А—Л–є –≤ —Н—В–Њ –≤—А–µ–Љ—П (—Б 1960 –њ–Њ 1966 –≥–Њ–і—Л) —А–∞–±–Њ—В–∞–ї –Ш–љ—Б—В–Є—В—Г—В–µ –Њ–±–Њ—А–Њ–љ–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞ (IDA), –≥–і–µ –Ј–∞–љ–Є–Љ–∞–ї—Б—П –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є—З–µ—Б–Ї–Є–Љ–Є –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П–Љ–Є. –Х–≥–Њ –њ–µ—А–≤–∞—П —А–∞–±–Њ—В–∞ –њ–Њ –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є—П–Љ –Њ—В–љ–Њ—Б–Є—В—Б—П –Ї 1966 –≥–Њ–і—Г[3], –Њ–і–љ–∞–Ї–Њ –Њ–љ–∞ –±—Л–ї–∞ –Ј–∞—Б–µ–Ї—А–µ—З–µ–љ–∞ –Є –≤ –Њ—В–Ї—А—Л—В–Њ–є –њ–µ—З–∞—В–Є –њ–Њ—П–≤–Є–ї–∞—Б—М —В–Њ–ї—М–Ї–Њ –≤ 1976 –≥–Њ–і—Г[4].
–Т 1960-—Е –≥–Њ–і–∞—Е –Т.–Р.–Х–ї–Є—Б–µ–µ–≤ –Є –Ю.–Я.–°—В–µ–њ—З–µ–љ–Ї–Њ–≤ –Ј–∞–љ–Є–Љ–∞–ї–Є—Б—М –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ–Љ –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є –≤ –°–°–°–†, –Њ–і–љ–∞–Ї–Њ –Є—Е —А–∞–±–Њ—В—Л –і–Њ —Б–Є—Е –њ–Њ—А –Ј–∞—Б–µ–Ї—А–µ—З–µ–љ—Л[1]. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –Њ–љ–Є –љ–∞–Ј—Л–≤–∞–ї–Є –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–Є "–Љ–Є–љ–Є–Љ–∞–ї—М–љ—Л–Љ–Є —Д—Г–љ–Ї—Ж–Є—П–Љ–Є" –Є –њ—А–µ–і–ї–Њ–ґ–Є–ї–Є –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є—О –Ь–∞–Ї–§–∞—А–ї–∞–љ–і–∞ –µ—Й–µ –≤ 1962 –≥–Њ–і—Г.
–°–≤–Њ–є—Б—В–≤–∞
–Э–µ–ї–Є–љ–µ–є–љ–Њ—Б—В—М –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є —Б —З–Є—Б–ї–Њ–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е n (n вАФ —З—С—В–љ–Њ–µ) –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ [1], [2]:
 .
.
–Ф–ї—П –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ –љ–µ–ї–Є–љ–µ–є–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є —Б –љ–µ—З—С—В–љ—Л–Љ —З–Є—Б–ї–Њ–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е —В–Њ—З–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –і–ї—П –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В–Є –љ–µ–Є–Ј–≤–µ—Б—В–љ–Њ[1].
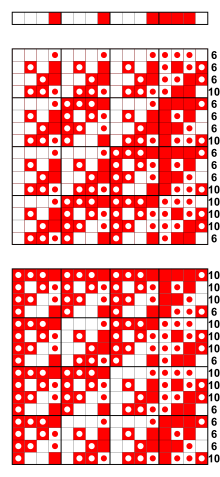
–Я—А–Є–Љ–µ—А—Л –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є
–Э–Є–ґ–µ –њ—А–Є–≤–µ–і–µ–љ—Л –њ—А–Є–Љ–µ—А—Л –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є —З–µ—В—Л—А—С—Е, —И–µ—Б—В–Є –Є –≤–Њ—Б—М–Љ–Є –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е[5].




–Ь–Њ–љ–Њ–≥—А–∞—Д–Є—П
–Т –Ї–љ–Є–≥–µ [1] –њ—А–Є–≤–µ–і–µ–љ –і–µ—В–∞–ї—М–љ—Л–є –Њ–±–Ј–Њ—А —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ –≤ –Њ–±–ї–∞—Б—В–Є –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є. –†–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ—В—Б—П –Є—Б—В–Њ—А–Є—П –Њ—В–Ї—А—Л—В–Є—П –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є, –Њ–њ–Є—Б—Л–≤–∞—О—В—Б—П –Є—Е –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П –≤ –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є–Є –Є –і–Є—Б–Ї—А–µ—В–љ–Њ–є –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ. –Ш—Б—Б–ї–µ–і—Г—О—В—Б—П –Њ—Б–љ–Њ–≤–љ—Л–µ —Б–≤–Њ–є—Б—В–≤–∞ –Є —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ—Л–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є, –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є–Є –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є –Њ—В –Љ–∞–ї–Њ–≥–Њ —З–Є—Б–ї–∞ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е, –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–љ—Л–µ –Є –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Є–µ –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–Є –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є, —Б–≤—П–Ј—М –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є —Б –і—А—Г–≥–Є–Љ–Є –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є—З–µ—Б–Ї–Є–Љ–Є —Б–≤–Њ–є—Б—В–≤–∞–Љ–Є. –Ш–Ј—Г—З–∞—О—В—Б—П —А–∞—Б—Б—В–Њ—П–љ–Є—П –Љ–µ–ґ–і—Г –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є—П–Љ–Є –Є –≥—А—Г–њ–њ–∞ –∞–≤—В–Њ–Љ–Њ—А—Д–Є–Ј–Љ–Њ–≤ –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є. –†–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—О—В—Б—П –≤–µ—А—Е–љ–Є–µ –Є –љ–Є–ґ–љ–Є–µ –Њ—Ж–µ–љ–Ї–Є —З–Є—Б–ї–∞ –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є –Є –≥–Є–њ–Њ—В–µ–Ј—Л –Њ –µ–≥–Њ –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Њ–Љ –Ј–љ–∞—З–µ–љ–Є–Є. –Я—А–Є–≤–Њ–і–Є—В—Б—П –і–µ—В–∞–ї—М–љ—Л–є —Б–Є—Б—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є –Њ–±–Ј–Њ—А 25 —А–∞–Ј–ї–Є—З–љ—Л—Е –Њ–±–Њ–±—Й–µ–љ–Є–є –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є–є, —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—О—В—Б—П –Њ—В–Ї—А—Л—В—Л–µ –≤–Њ–њ—А–Њ—Б—Л –≤ –і–∞–љ–љ–Њ–є –Њ–±–ї–∞—Б—В–Є. –Ъ–љ–Є–≥–∞ [1] 2015 –≥–Њ–і–∞ —Б–Њ–і–µ—А–ґ–Є—В –±–Њ–ї–µ–µ 125 —В–µ–Њ—А–µ–Љ –Њ –±–µ–љ—В-—Д—Г–љ–Ї—Ж–Є—П—Е –Є —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ —А–∞—Б—И–Є—А—П–µ—В –Ї–љ–Є–≥—Г [2] , –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ–љ—Г—О –≤ 2011 –≥–Њ–і—Г.
–Я—А–Є–Љ–µ—З–∞–љ–Є—П