Rebound-–∞—В–∞–Ї–∞ —П–≤–ї—П–µ—В—Б—П —В–µ—Е–љ–Њ–ї–Њ–≥–Є–µ–є –Ї—А–Є–њ—В–Њ–∞–љ–∞–ї–Є–Ј–∞ –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є—З–µ—Б–Ї–Є—Е —Е–µ—И-—Д—Г–љ–Ї—Ж–Є–є. –Т–њ–µ—А–≤—Л–µ —Н—В–∞ –∞—В–∞–Ї–∞ –±—Л–ї–∞ –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ–∞ –§–ї–Њ—А–Є–∞–љ–Њ–Љ –Ь–µ–љ–і–µ–ї–µ–Љ, –Ъ—А–Є—Б—В–Є–∞–љ–Њ–Љ –†–µ—З–±–µ—А–≥–µ—А–Њ–Љ, –Ь–∞—А—В–Є–љ–Њ–Љ –®–ї—Н—Д—Д–µ—А–Њ–Љ –Є –°–Њ—А–µ–љ–Њ–Љ –Ґ–Њ–Љ–њ—Б–Њ–љ–Њ–Љ –≤ 2009 –≥–Њ–і—Г. –Ю–љ–∞ –±—Л–ї–∞ –њ—А–µ–і–љ–∞–Ј–љ–∞—З–µ–љ–∞ –і–ї—П –∞—В–∞–Ї–Є AES-–њ–Њ–і–Њ–±–љ—Л—Е –∞–ї–≥–Њ—А–Є—В–Љ–Њ–≤ —В–∞–Ї–Є—Е, –Ї–∞–Ї Whirlpool –Є Gr√Єstl, –Њ–і–љ–∞–Ї–Њ –њ–Њ–Ј–ґ–µ –±—Л–ї–Њ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ –Њ–љ–∞ –њ—А–Є–Љ–µ–љ–Є–Љ–∞ —В–∞–Ї –ґ–µ –Є –Ї –і—А—Г–≥–Є–Љ –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є—П–Љ –Ї–∞–Ї Keccak, JH –Є Skein.
–Ю—Б–љ–Њ–≤–љ–∞—П –Є–і–µ—П
Rebound Attack вАФ —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–∞—П –∞—В–∞–Ї–∞ —Е–µ—И-—Д—Г–љ–Ї—Ж–Є–є —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ —А–Њ—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ[–∞–љ–≥–ї.] –Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ –Ї—А–Є–њ—В–Њ–∞–љ–∞–ї–Є–Ј–∞ –і–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Ї–Њ–ї–ї–Є–Ј–Є–є –Є —Г—П–Ј–≤–Є–Љ–Њ—Б—В–µ–є —Д—Г–љ–Ї—Ж–Є–є.
–Ю—Б–љ–Њ–≤–љ–Њ–є –Є–і–µ–µ–є –∞—В–∞–Ї–Є —П–≤–ї—П–µ—В—Б—П –Є–Ј—Г—З–µ–љ–Є–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –±–ї–Њ—З–љ–Њ–≥–Њ —И–Є—Д—А–∞ (–Є–ї–Є –µ–≥–Њ —Д—А–∞–≥–Љ–µ–љ—В–Њ–≤), –њ–µ—А–µ—Б—В–∞–љ–Њ–≤–Ї–Є –Є–ї–Є –і—А—Г–≥–Є—Е –љ–Є–Ј–Ї–Њ—Г—А–Њ–≤–љ–µ–≤—Л—Е –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є—З–µ—Б–Ї–Є—Е –∞–ї–≥–Њ—А–Є—В–Љ–Њ–≤. –Э–∞—Е–Њ–ґ–і–µ–љ–Є–µ –Ј–љ–∞—З–µ–љ–Є–є, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–Є—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞–Љ, –і–Њ—Б—В–Є–≥–∞–µ—В—Б—П —А–∞–Ј–і–µ–ї–µ–љ–Є–µ–Љ –њ—А–Є–Љ–Є—В–Є–≤–љ–Њ–≥–Њ –∞–ї–≥–Њ—А–Є—В–Љ–∞  –љ–∞ 3 —З–∞—Б—В–Є:
–љ–∞ 3 —З–∞—Б—В–Є:  .
.  вАФ –≤–љ—Г—В—А–µ–љ–љ—П—П —Д–∞–Ј–∞, –∞
вАФ –≤–љ—Г—В—А–µ–љ–љ—П—П —Д–∞–Ј–∞, –∞  –Є
–Є  –≤–Љ–µ—Б—В–µ —Б–Њ—Б—В–∞–≤–ї—П—О—В –≤–љ–µ—И–љ—О—О —Д–∞–Ј—Г. –Ч–ї–Њ—Г–Љ—Л—И–ї–µ–љ–љ–Є–Ї –≤—Л–±–Є—А–∞–µ—В –Ј–љ–∞—З–µ–љ–Є—П, –і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ–Њ —А–µ–∞–ї–Є–Ј—Г—О—Й–Є–µ —З–∞—Б—В—М –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≤–љ–µ—И–љ–µ–є —Д–∞–Ј—Л, –Є –і–Њ–њ–Њ–ї–љ—П–µ—В –Њ—Б—В–∞–≤—И—Г—О—Б—П —З–∞—Б—В—М —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≤ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ–Њ–є —Д–Њ—А–Љ–µ.
–≤–Љ–µ—Б—В–µ —Б–Њ—Б—В–∞–≤–ї—П—О—В –≤–љ–µ—И–љ—О—О —Д–∞–Ј—Г. –Ч–ї–Њ—Г–Љ—Л—И–ї–µ–љ–љ–Є–Ї –≤—Л–±–Є—А–∞–µ—В –Ј–љ–∞—З–µ–љ–Є—П, –і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ–Њ —А–µ–∞–ї–Є–Ј—Г—О—Й–Є–µ —З–∞—Б—В—М –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≤–љ–µ—И–љ–µ–є —Д–∞–Ј—Л, –Є –і–Њ–њ–Њ–ї–љ—П–µ—В –Њ—Б—В–∞–≤—И—Г—О—Б—П —З–∞—Б—В—М —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≤ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ–Њ–є —Д–Њ—А–Љ–µ.
Rebound-–∞—В–∞–Ї–∞ –≤–Ї–ї—О—З–∞–µ—В –≤ —Б–µ–±—П 2 —Н—В–∞–њ–∞:
- –Т–љ—Г—В—А–µ–љ–љ—П—П —Д–∞–Ј–∞ –Њ—Е–≤–∞—В—Л–≤–∞–µ—В —З–∞—Б—В—М –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї, –Ї–Њ—В–Њ—А—Л–µ —В—А—Г–і–љ–Њ –≤—Л–њ–Њ–ї–љ–Є—В—М –≤ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ–Њ–є —Д–Њ—А–Љ–µ. –Ч–і–µ—Б—М –њ—А–µ—Б–ї–µ–і—Г–µ—В—Б—П —Ж–µ–ї—М –љ–∞–є—В–Є –Љ–љ–Њ–≥–Њ —А–µ—И–µ–љ–Є–є –і–ї—П —Н—В–Њ–є —З–∞—Б—В–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї —Б –љ–Є–Ј–Ї–Њ–є —Б—А–µ–і–љ–µ–є –≤—А–µ–Љ–µ–љ–љ–Њ–є —Б–ї–Њ–ґ–љ–Њ—Б—В—М—О. –Ф–ї—П –і–Њ—Б—В–Є–ґ–µ–љ–Є—П —Н—В–Њ–є —Ж–µ–ї–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–∞—П —Б–Є—Б—В–µ–Љ–∞ —Г—А–∞–≤–љ–µ–љ–Є–є, –Њ–њ–Є—Б—Л–≤–∞—О—Й–∞—П —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї—Г –≤ —Н—В–Њ–є —Д–∞–Ј–µ, –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –љ–µ–і–Њ–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–є. –Я—А–Є –њ–Њ–Є—Б–Ї–µ —А–µ—И–µ–љ–Є—П –њ–Њ—П–≤–ї—П–µ—В—Б—П –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ —Б—В–µ–њ–µ–љ–µ–є —Б–≤–Њ–±–Њ–і—Л, –і–∞—О—Й–Є—Е –Љ–љ–Њ–≥–Њ –Њ—В–њ—А–∞–≤–љ—Л—Е —В–Њ—З–µ–Ї. –Т—Е–Њ–і–љ–∞—П —Д–∞–Ј–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ–Њ–≤—В–Њ—А–µ–љ–∞ –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —А–∞–Ј, —З—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М –і–Њ—Б—В–∞—В–Њ—З–љ–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —В–Њ—З–µ–Ї –і–ї—П —Г–і–∞—З–љ–Њ–≥–Њ –Є—Б–њ–Њ–ї–љ–µ–љ–Є—П –≤—Л—Е–Њ–і–љ–Њ–є —Д–∞–Ј—Л.
- –Т–Њ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј–µ –њ–Њ–і–Њ–±—А–∞–љ–љ—Л–µ –њ–∞—А—Л –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј—Л –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П –≤ –≤—Л—З–Є—Б–ї–µ–љ–Є—П—Е –≤ –њ—А—П–Љ–Њ–Љ –Є –Њ–±—А–∞—В–љ–Њ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є. –Ю–±—Л—З–љ–Њ
 –Є
–Є  –Є–Љ–µ—О—В –љ–Є–Ј–Ї—Г—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М, —В–∞–Ї —З—В–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ–Њ–≤—В–Њ—А—П—В—М –≤–љ—Г—В—А–µ–љ–љ—О—О —Д–∞–Ј—Г –і–ї—П –њ–Њ–ї—Г—З–µ–љ–Є—П –±–Њ–ї—М—И–µ–≥–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ —Б—В–∞—А—В–Њ–≤—Л—Е —В–Њ—З–µ–Ї.
–Є–Љ–µ—О—В –љ–Є–Ј–Ї—Г—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М, —В–∞–Ї —З—В–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ–Њ–≤—В–Њ—А—П—В—М –≤–љ—Г—В—А–µ–љ–љ—О—О —Д–∞–Ј—Г –і–ї—П –њ–Њ–ї—Г—З–µ–љ–Є—П –±–Њ–ї—М—И–µ–≥–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ —Б—В–∞—А—В–Њ–≤—Л—Е —В–Њ—З–µ–Ї.
–Я—А–µ–Є–Љ—Г—Й–µ—Б—В–≤–Њ –≤ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є –Њ–і–љ–Њ–є –≤—Е–Њ–і–љ–Њ–є –Є –і–≤—Г—Е –≤—Л—Е–Њ–і–љ—Л—Е —Д–∞–Ј –∞–ї–≥–Њ—А–Є—В–Љ–∞ –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є –±–Њ–ї–µ–µ —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ –Є —В–Њ—З–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М —Б–ї–Њ–ґ–љ—Л–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є. –≠—В–Њ—В –Љ–µ—В–Њ–і —П–≤–ї—П–µ—В—Б—П –±–Њ–ї–µ–µ —Н—Д—Д–µ–Ї—В–Є–≤–љ—Л–Љ, —З–µ–Љ —Б—В–∞–љ–і–∞—А—В–љ—Л–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ –Љ–µ—В–Њ–і—Л.
–Я–Њ–і—А–Њ–±–љ–Њ–µ –Њ–њ–Є—Б–∞–љ–Є–µ –∞—В–∞–Ї–Є —Е–µ—И-—Д—Г–љ–Ї—Ж–Є–є —Б –њ–Њ–Љ–Њ—Й—М—О AES-–њ–Њ–і–Њ–±–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є —Б–ґ–∞—В–Є—П
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Е–µ—И-—Д—Г–љ–Ї—Ж–Є–Є, –Є—Б–њ–Њ–ї—М–Ј—Г—О—Й–Є–µ AES-–њ–Њ–і–Њ–±–љ—Л–µ –±–ї–Њ—З–љ—Л–µ —И–Є—Д—А—Л –Ј–∞–Љ–µ—Й–µ–љ–Є—П –Є –њ–µ—А–µ—Б—В–∞–љ–Њ–≤–Ї–Є –Ї–∞–Ї —Д—Г–љ–Ї—Ж–Є–Є —Б–ґ–∞—В–Є—П. –≠—В–∞ —Д—Г–љ–Ї—Ж–Є—П —Б–ґ–∞—В–Є—П —Б–Њ—Б—В–Њ–Є—В –Є–Ј –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —А–∞—Г–љ–і–Њ–≤ S-–±–ї–Њ–Ї–Њ–≤ –Є –ї–Є–љ–µ–є–љ—Л—Е –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є. –У–ї–∞–≤–љ–Њ–є –Є–і–µ–µ–є –∞—В–∞–Ї–Є —П–≤–ї—П–µ—В—Б—П –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є, –Ї–Њ—В–Њ—А–∞—П –Є–Љ–µ–µ—В —Б–∞–Љ—Г—О —Б–ї–Њ–ґ–љ—Г—О –≤—Л—З–Є—Б–ї–Є—В–µ–ї—М–љ—Г—О —З–∞—Б—В—М –≤ —Б–µ—А–µ–і–Є–љ–µ. –≠—В–∞ —З–∞—Б—В—М –±—Г–і–µ—В –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –≤–Њ –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј–µ, –≤ —В–Њ –≤—А–µ–Љ—П –Ї–∞–Ї –±–Њ–ї–µ–µ –ї–µ–≥–Ї–Њ –≤—Л—З–Є—Б–ї—П–µ–Љ—Л–µ —З–∞—Б—В–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –±—Г–і—Г—В –≤ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј–µ. –°–Є—Б—В–µ–Љ–∞ —Г—А–∞–≤–љ–µ–љ–Є–є, –Њ–њ–Є—Б—Л–≤–∞—О—Й–Є—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –≤–Њ –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј–µ –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –љ–µ–і–Њ–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–є –і–ї—П –њ–Њ–ї—Г—З–µ–љ–Є—П –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –Њ—В–њ—А–∞–≤–љ—Л—Е —В–Њ—З–µ–Ї –≤ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј–µ. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –±–Њ–ї–µ–µ —В—А—Г–і–љ—Л–µ —З–∞—Б—В–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є —Б–Њ–і–µ—А–ґ–Є—В—Б—П –≤–Њ –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј–µ, –≤–Њ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј–µ –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П –њ—А–Њ—Б—В—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї.
–Т –љ–∞—З–∞–ї–µ –≤–љ—Г—В—А–µ–љ–љ—П—П —Д–∞–Ј–∞ –Є–Љ–µ–µ—В –љ–µ–±–Њ–ї—М—И–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –∞–Ї—В–Є–≤–љ—Л—Е(–љ–µ–љ—Г–ї–µ–≤—Л—Е) –±–∞–є—В–Њ–≤, –Ї —Б–µ—А–µ–і–Є–љ–µ –Є—Е —З–Є—Б–ї–Њ –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–µ—В, –∞ –≤ –Ї–Њ–љ—Ж–µ —Д–∞–Ј—Л —Б–љ–Њ–≤–∞ —Г–Љ–µ–љ—М—И–∞–µ—В—Б—П –і–Њ –Љ–∞–ї–Њ–≥–Њ —З–Є—Б–ї–∞. –Ю—Б–љ–Њ–≤–љ–∞—П –Є–і–µ—П –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ –њ–Њ–ї—Г—З–µ–љ–Є–Є –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –∞–Ї—В–Є–≤–љ—Л—Е –±–∞–є—В–Њ–≤ –љ–∞ –≤—Е–Њ–і–µ –Є –≤—Л—Е–Њ–і–µ S-–±–ї–Њ–Ї–∞ –≤ —Б–µ—А–µ–і–Є–љ–µ —Д–∞–Ј—Л. –•–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –Љ–Њ–≥—Г—В –±—Л—В—М —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ –≤—Л—З–Є—Б–ї–µ–љ—Л —Б –њ–Њ–Љ–Њ—Й—М—О –Ј–љ–∞—З–µ–љ–Є–є —А–∞–Ј–љ–Њ—Б—В–Є –≤ –љ–∞—З–∞–ї–µ –Є –Ї–Њ–љ—Ж–µ —Д–∞–Ј—Л –Є –њ–Њ–Є—Б–Ї–Њ–Љ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–є –љ–∞ –≤—Е–Њ–і–µ –Є –≤—Л—Е–Њ–і–µ S-–±–ї–Њ–Ї–∞.
–Т–Њ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј–µ –њ–Њ–і–Њ–±—А–∞–љ–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –њ—А–Њ–≤–µ—А—П—О—В—Б—П –≤ –њ—А—П–Љ–Њ–Љ –Є –Њ–±—А–∞—В–љ–Њ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є –і–ї—П –≤—Л—П–≤–ї–µ–љ–Є—П –Є—Е —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є—П –Є—Б–Ї–Њ–Љ—Л–Љ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–Љ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞–Љ. –Ю–±—Л—З–љ–Њ –Њ–љ–∞ –љ–∞—Ж–µ–ї–µ–љ–∞ –љ–∞ –њ–Њ–Є—Б–Ї —Н—Д—Д–µ–Ї—В–Є–≤–љ—Л—Е –њ–∞—А –Ј–љ–∞—З–µ–љ–Є–є —Г—Б–µ—З—С–љ–љ—Л—Е –∞–ї–≥–Њ—А–Є—В–Љ–Њ–≤, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –Є–Љ–µ–љ–љ–Њ —В–∞–Љ –Њ–љ–∞ –Є–Љ–µ–µ—В –љ–∞–Є–±–Њ–ї–µ–µ –≤—Л—Б–Њ–Ї—Г—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Г—Б–њ–µ—Е–∞. –Т–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Є—Б–Ї–Њ–Љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≤–Њ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј–µ –љ–∞–њ—А—П–Љ—Г—О –Ј–∞–≤–Є—Б–Є—В –Њ—В –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ –∞–Ї—В–Є–≤–љ—Л—Е –±–∞–є—В–Њ–≤ –Є –Є—Е —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–Є—П –≤ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–µ. –Ф–ї—П –і–Њ—Б—В–Є–ґ–µ–љ–Є—П –Ї–Њ–ї–ї–Є–Ј–Є–Є –љ–µ–і–Њ—Б—В–∞—В–Њ—З–љ–Њ –Є–Љ–µ—В—М —А–∞–Ј–љ–Њ—Б—В–Є –Ї–∞–Ї–Њ–≥–Њ-—В–Њ –Њ–њ—А–µ–і–µ–ї—С–љ–љ–Њ–≥–Њ —В–Є–њ–∞; –ї—О–±–Њ–є –∞–Ї—В–Є–≤–љ—Л–є –±–∞–є—В –љ–∞ –≤—Е–Њ–і–µ –Є –љ–∞ –≤—Л—Е–Њ–і–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –і–Њ–ї–ґ–µ–љ –Є–Љ–µ—В—М –Ј–љ–∞—З–µ–љ–Є–µ, –Њ—В–Љ–µ–љ—П—О—Й–µ–µ –≤—Б–µ –њ–Њ—Б–ї–µ–і—Г—О—Й–Є–µ –Њ–њ–µ—А–∞—Ж–Є–Є –∞–ї–≥–Њ—А–Є—В–Љ–∞. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ—А–Є –њ—А–Њ–µ–Ї—В–Є—А–Њ–≤–∞–љ–Є–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –ї—О–±–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –∞–Ї—В–Є–≤–љ—Л—Е –±–∞–є—В –≤ –љ–∞—З–∞–ї–µ –Є –≤ –Ї–Њ–љ—Ж–µ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј—Л –і–Њ–ї–ґ–љ–Њ –±—Л—В—М –≤ –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ–Љ –њ–Њ–ї–Њ–ґ–µ–љ–Є–Є. –Я–Њ–ї—Г—З–µ–љ–Є–µ —В–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є–є –±–∞–є—В–Њ–≤ —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –њ–Њ–ї—Г—З–µ–љ–Є—П —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≤–љ–µ—И–љ–µ–є —Д–∞–Ј—Л.
–Т —Ж–µ–ї–Њ–Љ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Б–≥–µ–љ–µ—А–Є—А–Њ–≤–∞—В—М —В–∞–Ї–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј—Л, —З—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М –±–Њ–ї—М—И–µ –Њ–і–љ–Њ–≥–Њ –Њ–ґ–Є–і–∞–µ–Љ–Њ–≥–Њ –љ–∞–±–Њ—А–∞ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≤–љ–µ—И–љ–µ–є —Д–∞–Ј—Л. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –µ—Б—В—М –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –њ–Њ–ї—Г—З–µ–љ–Є—П –њ–Њ—З—В–Є-–Ї–Њ–ї–ї–Є–Ј–Є–Є, –≥–і–µ –љ–µ–Ї–Њ—В–Њ—А—Л–µ –∞–Ї—В–Є–≤–љ—Л–µ –±–∞–є—В—Л –≤ –љ–∞—З–∞–ї–µ –Є –Ї–Њ–љ—Ж–µ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј—Л –љ–µ –Њ—В–Љ–µ–љ—П—О—В –і–∞–ї—М–љ–µ–є—И–Є–µ –і–µ–є—Б—В–≤–Є—П –∞–ї–≥–Њ—А–Є—В–Љ–∞.
–Я—А–Є–Љ–µ—А –∞—В–∞–Ї–Є –љ–∞ Whirlpool
Rebound-–∞—В–∞–Ї–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–∞ –љ–∞ —Е–µ—И-—Д—Г–љ–Ї—Ж–Є–Є Whirlpool –і–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Ї–Њ–ї–ї–Є–Ј–Є–є –Ј–∞ 4.5 –Є–ї–Є 5.5 —А–∞—Г–љ–і–Њ–≤. –Я–Њ—З—В–Є-–Ї–Њ–ї–ї–Є–Ј–Є–Є –Љ–Њ–≥—Г—В –±—Л—В—М –Њ–±–љ–∞—А—Г–ґ–µ–љ—Л –Ј–∞ 6.5 –Є 7.5 —А–∞—Г–љ–і–Њ–≤. –Э–Є–ґ–µ –Њ–њ–Є—Б–∞–љ–∞ 4.5-—А–∞—Г–љ–і–Њ–≤–∞—П –∞—В–∞–Ї–∞.
–Я—А–µ–і–≤–∞—А–Є—В–µ–ї—М–љ—Л–µ –≤—Л—З–Є—Б–ї–µ–љ–Є—П
| –І–Є—Б–ї–Њ —А–µ—И–µ–љ–Є–є |
–І–∞—Б—В–Њ—В–∞
|
| 0 |
39655
|
| 2 |
20018
|
| 4 |
5043
|
| 6 |
740
|
| 8 |
79
|
| 256 |
1
|
–І—В–Њ–±—Л —Б–і–µ–ї–∞—В—М rebound-–∞—В–∞–Ї—Г –±–Њ–ї–µ–µ —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ–є, —В–∞–±–ї–Є—Ж–∞ –і–ї—П —А–∞–Ј–љ–Њ—Б—В–µ–є S-–±–ї–Њ–Ї–∞ –≤—Л—З–Є—Б–ї—П–µ—В—Б—П –і–Њ –љ–∞—З–∞–ї–∞ –∞—В–∞–Ї–Є. –Я—Г—Б—В—М  –Њ–Ј–љ–∞—З–∞–µ—В S-–±–ї–Њ–Ї. –Ч–∞—В–µ–Љ –і–ї—П –Ї–∞–ґ–і–Њ–є –њ–∞—А—Л
–Њ–Ј–љ–∞—З–∞–µ—В S-–±–ї–Њ–Ї. –Ч–∞—В–µ–Љ –і–ї—П –Ї–∞–ґ–і–Њ–є –њ–∞—А—Л  –Љ—Л –љ–∞–є–і—С–Љ —А–µ—И–µ–љ–Є—П
–Љ—Л –љ–∞–є–і—С–Љ —А–µ—И–µ–љ–Є—П  (–њ—А–Є –Є—Е –љ–∞–ї–Є—З–Є–Є) —Б–ї–µ–і—Г—О—Й–µ–≥–Њ —А–∞–≤–µ–љ—Б—В–≤–∞
(–њ—А–Є –Є—Е –љ–∞–ї–Є—З–Є–Є) —Б–ї–µ–і—Г—О—Й–µ–≥–Њ —А–∞–≤–µ–љ—Б—В–≤–∞
 ,
,
–≥–і–µ  вАФ —А–∞–Ј–љ–Њ—Б—В—М –љ–∞ –≤—Е–Њ–і–µ, –∞
вАФ —А–∞–Ј–љ–Њ—Б—В—М –љ–∞ –≤—Е–Њ–і–µ, –∞  вАФ —А–∞–Ј–љ–Њ—Б—В—М –љ–∞ –≤—Л—Е–Њ–і–µ S-–±–ї–Њ–Ї–∞. –≠—В–∞ —В–∞–±–ї–Є—Ж–∞ 256—Е256 –њ–Њ–Ј–≤–Њ–ї—П–µ—В –љ–∞–є—В–Є –Ј–љ–∞—З–µ–љ–Є—П, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–Є–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞–Љ –і–ї—П –≤—Б–µ—Е –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –њ–∞—А, –њ—А–Њ—Е–Њ–і—П—Й–Є—Е —З–µ—А–µ–Ј S-–±–ї–Њ–Ї. –Ґ–∞–±–ї–Є—Ж–∞ —Б–њ—А–∞–≤–∞ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ–µ —З–Є—Б–ї–Њ —А–µ—И–µ–љ–Є–є –Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Є—Е –њ–Њ—П–≤–ї–µ–љ–Є—П. –Я–µ—А–≤–∞—П —Б—В—А–Њ–Ї–∞ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В —Б–ї—Г—З–∞–є –Њ—В—Б—Г—В—Б—В–≤–Є—П —А–µ—И–µ–љ–Є–є, –њ–Њ—Б–ї–µ–і–љ—П—П –Њ–њ–Є—Б—Л–≤–∞–µ—В —Б–ї—Г—З–∞–є —Б –љ—Г–ї–µ–≤–Њ–є —А–∞–Ј–љ–Њ—Б—В—М—О.
вАФ —А–∞–Ј–љ–Њ—Б—В—М –љ–∞ –≤—Л—Е–Њ–і–µ S-–±–ї–Њ–Ї–∞. –≠—В–∞ —В–∞–±–ї–Є—Ж–∞ 256—Е256 –њ–Њ–Ј–≤–Њ–ї—П–µ—В –љ–∞–є—В–Є –Ј–љ–∞—З–µ–љ–Є—П, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–Є–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞–Љ –і–ї—П –≤—Б–µ—Е –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –њ–∞—А, –њ—А–Њ—Е–Њ–і—П—Й–Є—Е —З–µ—А–µ–Ј S-–±–ї–Њ–Ї. –Ґ–∞–±–ї–Є—Ж–∞ —Б–њ—А–∞–≤–∞ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ–µ —З–Є—Б–ї–Њ —А–µ—И–µ–љ–Є–є –Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Є—Е –њ–Њ—П–≤–ї–µ–љ–Є—П. –Я–µ—А–≤–∞—П —Б—В—А–Њ–Ї–∞ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В —Б–ї—Г—З–∞–є –Њ—В—Б—Г—В—Б—В–≤–Є—П —А–µ—И–µ–љ–Є–є, –њ–Њ—Б–ї–µ–і–љ—П—П –Њ–њ–Є—Б—Л–≤–∞–µ—В —Б–ї—Г—З–∞–є —Б –љ—Г–ї–µ–≤–Њ–є —А–∞–Ј–љ–Њ—Б—В—М—О.
–Т—Л–њ–Њ–ї–љ–µ–љ–Є–µ –∞—В–∞–Ї–Є
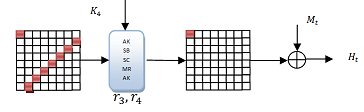
–Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Ї–Њ–ї–ї–Є–Ј–Є–Є –≤ Whirlpool –Ј–∞ 4.5 —А–∞—Г–љ–і–∞, –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –≤ —В–∞–±–ї–Є—Ж–µ –љ–Є–ґ–µ –і–Њ–ї–ґ–љ—Л –±—Л—В—М –≤—Л—З–Є—Б–ї–µ–љ—Л. –•–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ —Б –љ–∞–Є–Љ–µ–љ—М—И–Є–Љ —З–Є—Б–ї–Њ–Љ –∞–Ї—В–Є–≤–љ—Л—Е –±–∞–є—В–Њ–≤ –Њ—В–Љ–µ—З–µ–љ–∞ –Ї—А–∞—Б–љ—Л–Љ. –•–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ–Є—Б–∞–љ–∞ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ–Љ –∞–Ї—В–Є–≤–љ—Л—Е –±–∞–є—В–Њ–≤ –≤ –Ї–∞–ґ–і–Њ–Љ —А–∞—Г–љ–і–µ, –љ–∞–њ—А–Є–Љ–µ—А, 1 вЖТ 8 вЖТ 64 вЖТ 8 вЖТ 1 вЖТ 1.
–£—Б–µ—З–µ–љ–љ–∞—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ –≤ 4.5 —А–∞—Г–љ–і–∞—Е —Е–µ—И-—Д—Г–љ–Ї—Ж–Є–Є Whirlpool.
 |
![]()
|
 |

|
 |
|
–Т–љ—Г—В—А–µ–љ–љ—П—П —Д–∞–Ј–∞
–¶–µ–ї—М –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј—Л –і–Њ–њ–Њ–ї–љ–Є—В—М —А–∞–Ј–љ–Њ—Б—В–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –љ–∞ —Н—В–∞–њ–µ 8 вЖТ 64 вЖТ 8. –≠—В–Њ –Љ–Њ–ґ–µ—В –±—Л—В—М –≤—Л–њ–Њ–ї–љ–µ–љ–Њ –≤ 3 —И–∞–≥–∞:
- –Т—Л–±—А–∞—В—М –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–µ –љ–µ–љ—Г–ї–µ–≤–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –і–ї—П 8 –∞–Ї—В–Є–≤–љ—Л—Е –±–∞–є—В –љ–∞ –≤—Л—Е–Њ–і–µ –Њ–њ–µ—А–∞—Ж–Є–Є –ї–Є–љ–µ–є–љ–Њ–є –і–Є—Д—Д—Г–Ј–Є–Є –≤ —А–∞—Г–љ–і–µ 3. –≠—В–Є —А–∞–Ј–ї–Є—З–Є—П –Ј–∞—В–µ–Љ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ—П—О—Й–Є—Е—Б—П –≤ –Њ–±—А–∞—В–љ–Њ–Љ –Ї –≤—Л—Е–Њ–і—Г –Њ–њ–µ—А–∞—Ж–Є–Є —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Њ–є –њ–µ—А–µ—Б—В–∞–љ–Њ–≤–Ї–Є –≤ —А–∞—Г–љ–і–µ 3. –Ш–Ј-–Ј–∞ —Б–≤–Њ–є—Б—В–≤ –Њ–њ–µ—А–∞—Ж–Є–Є –ї–Є–љ–µ–є–љ–Њ–є –і–Є—Д—Д—Г–Ј–Є–Є, –≤—Б–µ –±–∞–є—В—Л —Б—В–∞–љ–Њ–≤—П—В—Б—П –∞–Ї—В–Є–≤–љ—Л–Љ–Є. –≠—В–Њ –Љ–Њ–ґ–µ—В –±—Л—В—М —Б–і–µ–ї–∞–љ–Њ –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ –і–ї—П –Ї–∞–ґ–і–Њ–є —Б—В—А–Њ–Ї–Є.
- –Т—Л–±—А–∞—В—М –Ј–љ–∞—З–µ–љ–Є–µ –і–ї—П –Ї–∞–ґ–і–Њ–≥–Њ –∞–Ї—В–Є–≤–љ–Њ–≥–Њ –±–∞–є—В–∞ –љ–∞ –≤—Е–Њ–і–µ –Њ–њ–µ—А–∞—Ж–Є–Є –ї–Є–љ–µ–є–љ–Њ–є –і–Є—Д—Д—Г–Ј–Є–Є –≤–Њ 2 —А–∞—Г–љ–і–µ –Є —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–Є—В—М —Н—В–Є —А–∞–Ј–ї–Є—З–Є—П –≤–њ–µ—А–µ–і –љ–∞ –≤—Е–Њ–і –Њ–њ–µ—А–∞—Ж–Є–Є —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Њ–є –њ–µ—А–µ—Б—В–∞–љ–Њ–≤–Ї–Є –≤ —А–∞—Г–љ–і–µ 3. –°–і–µ–ї–∞—В—М —Н—В–Њ –і–ї—П –≤—Б–µ—Е 255 –љ–µ–љ—Г–ї–µ–≤—Л—Е —А–∞–Ј–ї–Є—З–Є–є –Ї–∞–ґ–і–Њ–≥–Њ –±–∞–є—В–∞. –Ю–њ—П—В—М –ґ–µ, —Н—В–Њ –Љ–Њ–ґ–µ—В –±—Л—В—М —Б–і–µ–ї–∞–љ–Њ –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ –і–ї—П –Ї–∞–ґ–і–Њ–є —Б—В—А–Њ–Ї–Є.
- –Т–Њ –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј–µ —Б –њ–Њ–Љ–Њ—Й—М—О —В–∞–±–ї–Є—Ж—Л —А–∞–Ј–љ–Њ—Б—В–µ–є(DDT) –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–µ –≤—Е–Њ–і–љ—Л—Е –Є –≤—Л—Е–Њ–і–љ—Л—Е —А–∞–Ј–љ–Њ—Б—В–µ–є (–Ї–∞–Ї –љ–∞–є–і–µ–љ–Њ –≤ —И–∞–≥–µ 1 –Є 2) –Њ–њ–µ—А–∞—Ж–Є–Є —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Њ–є –њ–µ—А–µ—Б—В–∞–љ–Њ–≤–Ї–Є –≤ 3 —А–∞—Г–љ–і–µ. –Ъ–∞–ґ–і–∞—П —Б—В—А–Њ–Ї–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–Њ–≤–µ—А–µ–љ–∞ –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ, –Є –Њ–ґ–Є–і–∞–µ—В—Б—П 2 —А–µ—И–µ–љ–Є—П –љ–∞ –Ї–∞–ґ–і—Л–є S-–±–ї–Њ–Ї. –Т –Њ–±—Й–µ–є —Б–ї–Њ–ґ–љ–Њ—Б—В–Є, –Њ–ґ–Є–і–∞–µ–Љ–Њ–µ —З–Є—Б–ї–Њ –Ј–љ–∞—З–µ–љ–Є–є, –Ї–Њ—В–Њ—А—Л–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—В –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–µ вАФ 264.
–≠—В–Є —И–∞–≥–Є –Љ–Њ–ґ–љ–Њ –њ–Њ–≤—В–Њ—А–Є—В—М —Б 264 —А–∞–Ј–ї–Є—З–љ—Л–Љ–Є –Є—Б—Е–Њ–і–љ—Л–Љ–Є –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є –љ–∞ —И–∞–≥–µ 1, –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ —З–µ–≥–Њ –≤ –Њ–±—Й–µ–є —Б–ї–Њ–ґ–љ–Њ—Б—В–Є –њ–Њ–ї—Г—З–∞–µ—В—Б—П 2128 –Ј–љ–∞—З–µ–љ–Є–є, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–Є—Е –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–µ –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј—Л. –Ъ–∞–ґ–і—Л–є –љ–∞–±–Њ—А 264 –Ј–љ–∞—З–µ–љ–Є–є –Љ–Њ–ґ–µ—В –±—Л—В—М –љ–∞–є–і–µ–љ —Б–Њ —Б–ї–Њ–ґ–љ–Њ—Б—В—М—О –≤ 28 —А–∞—Г–љ–і–Њ–≤ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є –≤ —Б–≤—П–Ј–Є —Б —И–∞–≥–Њ–Љ –њ—А–µ–і–≤—Л—З–Є—Б–ї–µ–љ–Є—П.
–Т–љ–µ—И–љ—П—П —Д–∞–Ј–∞
–Т–љ–µ—И–љ—П—П —Д–∞–Ј–∞ –і–Њ–њ–Њ–ї–љ—П–µ—В –і–∞–љ–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–љ—Л–Љ –њ—Г—В—С–Љ. –Ю–љ–∞ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В —Г—Б–µ—З—С–љ–љ—Л–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—Л –≤ –Њ—В–ї–Є—З–Є–µ –Њ—В –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј—Л. –Ъ–∞–ґ–і–∞—П —В–Њ—З–Ї–∞ –Њ—В—Б—З—С—В–∞ —Б—З–Є—В–∞–µ—В—Б—П –≤ –њ—А—П–Љ–Њ–Љ –Є –Њ–±—А–∞—В–љ–Њ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є. –І—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М –Є—Б—Е–Њ–і–љ—Л–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є, 8 –∞–Ї—В–Є–≤–љ—Л—Е –±–∞–є—В–Њ–≤ –і–Њ–ї–ґ–љ—Л –Њ–±—А–∞–Ј–Њ–≤–∞—В—М 1 –∞–Ї—В–Є–≤–љ—Л–є –±–∞–є—В –≤ –Њ–±–Њ–Є—Е –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П—Е. –Я—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ 8 –±–∞–є—В–Њ–≤ –≤ 1 —Б–ї—Г—З–∞–µ—В—Б—П —Б –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О –≤ 2вИТ56,[1], –њ–Њ—Н—В–Њ–Љ—Г –њ–Њ–ї—Г—З–µ–љ–Є–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –Є–Љ–µ–µ—В —И–∞–љ—Б 2вИТ112. –І—В–Њ–±—Л –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –Ї–Њ–ї–ї–Є–Ј–Є—О, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, —З—В–Њ–±—Л –±–∞–є—В—Л –љ–∞ –≤—Е–Њ–і–µ –Є –љ–∞ –≤—Л—Е–Њ–і–µ –±–ї–Њ–Ї–Є—А–Њ–≤–∞–ї–Є –≤—Б–µ –њ–Њ—Б–ї–µ–і—Г—О—Й–Є–µ –Њ–њ–µ—А–∞—Ж–Є–Є. –≠—В–Њ –њ—А–Њ–Є—Б—Е–Њ–і–Є—В —Б –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї—М–љ–Њ 2вИТ8, –≤ –Њ–±—Й–µ–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Г—Б–њ–µ—Е–∞ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј—Л —Б–Њ—Б—В–∞–≤–ї—П–µ—В 2вИТ120.
–Ф–ї—П –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –Ї–Њ–ї–ї–Є–Ј–Є–Є, –≤–Њ –≤–љ—Г—В—А–µ–љ–љ–µ–є —Д–∞–Ј–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Б–≥–µ–љ–µ—А–Є—А–Њ–≤–∞—В—М —Е–Њ—В—П –±—Л 2120 —В–Њ—З–µ–Ї. –Я–Њ—Б–ї–µ —Н—В–Њ–≥–Њ –Њ–њ–µ—А–∞—Ж–Є—П –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –Љ–Њ–ґ–µ—В –≤—Л–њ–Њ–ї–љ—П—В—М—Б—П —Б–Њ –≤—А–µ–Љ–µ–љ–љ–Њ–є —Б–ї–Њ–ґ–љ–Њ—Б—В—М—О 1 –љ–∞ –Њ–і–љ—Г —Б—В–∞—А—В–Њ–≤—Г—О —В–Њ—З–Ї—Г,[2] –њ–Њ—В–Њ–Љ—Г –Є—В–Њ–≥–Њ–≤–∞—П –≤—А–µ–Љ–µ–љ–љ–∞—П —Б–ї–Њ–ґ–љ–Њ—Б—В—М –∞—В–∞–Ї–Є вАФ 2120.
–£—Б–Њ–≤–µ—А—И–µ–љ—Б—В–≤–Њ–≤–∞–љ–Є–µ –∞—В–∞–Ї–Є
–С–∞–Ј–Њ–≤–∞—П 4.5-—А–∞—Г–љ–і–Њ–≤–∞—П –∞—В–∞–Ї–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М —Г–ї—Г—З—И–µ–љ–∞ –і–Њ 5.5-—А–∞—Г–љ–і–Њ–≤–Њ–є –і–Њ–±–∞–≤–ї–µ–љ–Є–µ–Љ –µ—Й—С 1 —А–∞—Г–љ–і–∞ –≤–Њ –≤–љ—Г—В—А–µ–љ–љ—О—О —Д–∞–Ј—Г. –≠—В–Њ –њ–Њ–≤—Л—Б–Є—В –≤—А–µ–Љ–µ–љ–љ—Г—О —Б–ї–Њ–ґ–љ–Њ—Б—В—М –∞–ї–≥–Њ—А–Є—В–Љ–∞ –і–Њ 2184.[3]
–£—Б–Њ–≤–µ—А—И–µ–љ—Б—В–≤–Њ–≤–∞–љ–Є–µ –≤–љ–µ—И–љ–µ–є —Д–∞–Ј—Л —Б –µ—С –љ–∞—З–∞–ї–Њ–Љ –Є –Њ–Ї–Њ–љ—З–∞–љ–Є–µ–Љ —Б 8 –∞–Ї—В–Є–≤–љ—Л–Љ–Є –±–∞–є—В–∞–Љ–Є –њ—А–Є–≤–µ–ї–Њ –Ї –њ–Њ—З—В–Є-–Ї–Њ–ї–ї–Є–Ј–Є–Є –≤ 52 –±–∞–є—В–∞—Е Whirlpool, –њ—А–Њ–і–ї–µ–≤–∞—О—Й–µ–є –∞—В–∞–Ї—Г –і–Њ 7.5 —А–∞—Г–љ–і–Њ–≤ —Б –≤—А–µ–Љ–µ–љ–љ–Њ–є —Б–ї–Њ–ґ–љ–Њ—Б—В—М—О 2192.[3]
–Я—А–µ–і–њ–Њ–ї–∞–≥–∞—П, —З—В–Њ –Ј–ї–Њ—Г–Љ—Л—И–ї–µ–љ–љ–Є–Ї –Є–Љ–µ–µ—В –Ї–Њ–љ—В—А–Њ–ї—М –љ–∞–і –Ј–љ–∞—З–µ–љ–Є–µ–Љ —Ж–µ–њ–Њ—З–Ї–Є –Є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≤—Е–Њ–і –≤ –Ї–ї—О—З–µ–≤–Њ–є –≥—А–∞—Д–Є–Ї Whirlpool, –∞—В–∞–Ї–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–Њ–і–ї–µ–љ–∞ –і–Њ 9.5 —А–∞—Г–љ–і–Њ–≤ —Б —Г—Б–ї–Њ–≤–љ–Њ-—Б–≤–Њ–±–Њ–і–љ–Њ–є –Ї–Њ–ї–ї–Є–Ј–Є–µ–є –≤ 52 –±–∞–є—В–∞—Е —Б –≤—А–µ–Љ–µ–љ–љ–Њ–є —Б–ї–Њ–ґ–љ–Њ—Б—В—М—О 2128.[4]
–Я—А–Є–Љ–µ—З–∞–љ–Є—П
- вЖС Lamberger, Mendel, Rechberger, Rijmen, Schl√§ffer, 2010, p. 18
- вЖС Lamberger, Mendel, Rechberger, Rijmen, Schl√§ffer, 2010, p. 22
- вЖС 1 2 Lamberger, Mendel, Rechberger, Rijmen, Schl√§ffer, 2010, p. 25
- вЖС Lamberger, Mendel, Rechberger, Rijmen, Schl√§ffer, 2010, p. 31
–Ы–Є—В–µ—А–∞—В—Г—А–∞
- The Rebound Attack: Cryptanalysis of Reduced Whirlpool and Gr√Єstl by Florian Mendel, Christian Rechberger, Martin Schlaffer, and Soren S. Thomsen (Fast Software Encryption 2009: 260вАФ276)
- The Rebound Attack on Reduced Gr√Єstl Hash Function by Florian Mendel, Christian Rechberger, Martin Schlaffer, and Soren S. Thomsen (The CryptographerвАЩs Track at RSA Conference 2010: 350вАФ365)
- Unaligned Rebound Attack вАФ Application to Keccak by Alexandre Duc, Jian Guo, Thomas Peyrin, Lei Wei (IACR Cryptology ePrint Archive Year 2011 / 420)
- How to Improve Rebound Attacks by Mar√≠a Naya-Plasencia FHNW, Windisch, Switzerland (CRYPTOвАЩ11 Proceedings of the 31st annual conference on Advances in cryptology Pages 188вАФ205)
- The Rebound Attack and Subspace Distinguishers: Application to Whirlpool by Mario Lamberger, Florian Mendel, Christian Rechberger, Vincent Rijmen, and Martin Schläffer(IACR Cryptology ePrint Archive, Year. 2010 /198).
- Cryptanalysis of AES based hash functions A PHd theses by Martin Schläffer