–°—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–∞—П –Љ–Њ—Й–љ–Њ—Б—В—М –≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —Б—В–∞—В–Є—Б—В–Є–Ї–µ вАФ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—Б–љ–Њ–≤–љ–Њ–є (–Є–ї–Є –љ—Г–ї–µ–≤–Њ–є) –≥–Є–њ–Њ—В–µ–Ј—Л –њ—А–Є –њ—А–Њ–≤–µ—А–Ї–µ —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Є—Е –≥–Є–њ–Њ—В–µ–Ј –≤ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞ –Ї–Њ–љ–Ї—Г—А–Є—А—Г—О—Й–∞—П (–Є–ї–Є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–∞—П) –≥–Є–њ–Њ—В–µ–Ј–∞ –≤–µ—А–љ–∞. –І–µ–Љ –≤—Л—И–µ –Љ–Њ—Й–љ–Њ—Б—В—М —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–≥–Њ —В–µ—Б—В–∞, —В–µ–Љ –Љ–µ–љ—М—И–µ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–µ—А—И–Є—В—М –Њ—И–Є–±–Ї—Г –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞. –Т–µ–ї–Є—З–Є–љ–∞ –Љ–Њ—Й–љ–Њ—Б—В–Є —В–∞–Ї–ґ–µ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П —А–∞–Ј–Љ–µ—А–∞ –≤—Л–±–Њ—А–Ї–Є, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ–є –і–ї—П –њ–Њ–і—В–≤–µ—А–ґ–і–µ–љ–Є—П –≥–Є–њ–Њ—В–µ–Ј—Л —Б –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ–є —Б–Є–ї–Њ–є —Н—Д—Д–µ–Ї—В–∞.
–Я—А–Є–Љ–µ–љ–µ–љ–Є–µ
–Т–µ–ї–Є—З–Є–љ–∞ –Љ–Њ—Й–љ–Њ—Б—В–Є –њ—А–Є –њ—А–Њ–≤–µ—А–Ї–µ —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л –Ј–∞–≤–Є—Б–Є—В –Њ—В —Б–ї–µ–і—Г—О—Й–Є—Е —Д–∞–Ї—В–Њ—А–Њ–≤:
- –≤–µ–ї–Є—З–Є–љ—Л —Г—А–Њ–≤–љ—П –Ј–љ–∞—З–Є–Љ–Њ—Б—В–Є, –Њ–±–Њ–Ј–љ–∞—З–∞–µ–Љ–Њ–≥–Њ –≥—А–µ—З–µ—Б–Ї–Њ–є –±—Г–Ї–≤–Њ–є
 , –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Ї–Њ—В–Њ—А–Њ–≥–Њ –њ—А–Є–љ–Є–Љ–∞–µ—В—Б—П —А–µ—И–µ–љ–Є–µ –Њ–± –Њ—В–≤–µ—А–ґ–µ–љ–Є–Є –Є–ї–Є –њ—А–Є–љ—П—В–Є–Є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л;
, –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Ї–Њ—В–Њ—А–Њ–≥–Њ –њ—А–Є–љ–Є–Љ–∞–µ—В—Б—П —А–µ—И–µ–љ–Є–µ –Њ–± –Њ—В–≤–µ—А–ґ–µ–љ–Є–Є –Є–ї–Є –њ—А–Є–љ—П—В–Є–Є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л;
- –≤–µ–ї–Є—З–Є–љ—Л —Н—Д—Д–µ–Ї—В–∞ (—В–Њ –µ—Б—В—М —А–∞–Ј–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б—А–∞–≤–љ–Є–≤–∞–µ–Љ—Л–Љ–Є —Б—А–µ–і–љ–Є–Љ–Є);
- —А–∞–Ј–Љ–µ—А–∞ –≤—Л–±–Њ—А–Ї–Є, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ–є –і–ї—П –њ–Њ–і—В–≤–µ—А–ґ–і–µ–љ–Є—П —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л.
–Ю—Б–љ–Њ–≤–љ—Л–µ –њ–∞—А–∞–Љ–µ—В—А—Л –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Љ–Њ—Й–љ–Њ—Б—В–Є –њ–Њ–Ї–∞–Ј–∞–љ—Л –љ–∞ —Б—Е–µ–Љ–µ.
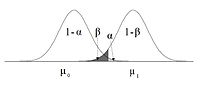 –°—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–∞—П –Љ–Њ—Й–љ–Њ—Б—В—М –°—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–∞—П –Љ–Њ—Й–љ–Њ—Б—В—М
|
|
–£—А–Њ–≤–µ–љ—М –Ј–љ–∞—З–Є–Љ–Њ—Б—В–Є ( ) –≤—Л–±–Є—А–∞–µ—В—Б—П –Є—Б—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–µ–Љ –Є –Њ–њ—А–µ–і–µ–ї—П–µ—В –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–µ—А—И–µ–љ–Є—П –Њ—И–Є–±–Ї–Є –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞. –Т–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–∞—П –≥–Є–њ–Њ—В–µ–Ј–∞ –≤–µ—А–љ–∞, –љ–Њ —А–µ—И–µ–љ–Є–µ –њ—А–Є–љ–Є–Љ–∞–µ—В—Б—П –≤ –њ–Њ–ї—М–Ј—Г –љ—Г–ї–µ–≤–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л (–Њ—И–Є–±–Ї–∞ –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞), –Њ–±–Њ–Ј–љ–∞—З–∞–µ—В—Б—П –≥—А–µ—З–µ—Б–Ї–Њ–є –±—Г–Ї–≤–Њ–є
) –≤—Л–±–Є—А–∞–µ—В—Б—П –Є—Б—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–µ–Љ –Є –Њ–њ—А–µ–і–µ–ї—П–µ—В –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–µ—А—И–µ–љ–Є—П –Њ—И–Є–±–Ї–Є –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞. –Т–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–∞—П –≥–Є–њ–Њ—В–µ–Ј–∞ –≤–µ—А–љ–∞, –љ–Њ —А–µ—И–µ–љ–Є–µ –њ—А–Є–љ–Є–Љ–∞–µ—В—Б—П –≤ –њ–Њ–ї—М–Ј—Г –љ—Г–ї–µ–≤–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л (–Њ—И–Є–±–Ї–∞ –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞), –Њ–±–Њ–Ј–љ–∞—З–∞–µ—В—Б—П –≥—А–µ—З–µ—Б–Ї–Њ–є –±—Г–Ї–≤–Њ–є  . –Ґ–Њ–≥–і–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –њ—А–Є–љ—П—В–Є—П –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ —А–µ—И–µ–љ–Є—П –њ—А–Є –Є—Б—В–Є–љ–љ–Њ–є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј–µ (–Љ–Њ—Й–љ–Њ—Б—В—М) —А–∞–≤–љ–∞
. –Ґ–Њ–≥–і–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –њ—А–Є–љ—П—В–Є—П –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ —А–µ—И–µ–љ–Є—П –њ—А–Є –Є—Б—В–Є–љ–љ–Њ–є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј–µ (–Љ–Њ—Й–љ–Њ—Б—В—М) —А–∞–≤–љ–∞  .
.
–Я—А–Є –Є–Ј–≤–µ—Б—В–љ–Њ–Љ —Б—В–∞–љ–і–∞—А—В–љ–Њ–Љ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–Є –≥–µ–љ–µ—А–∞–ї—М–љ–Њ–є —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В–Є –Є –Ј–∞–і–∞–љ–љ–Њ–Љ —Г—А–Њ–≤–љ–µ –Ј–љ–∞—З–Є–Љ–Њ—Б—В–Є  –Љ–Њ—Й–љ–Њ—Б—В—М
–Љ–Њ—Й–љ–Њ—Б—В—М  –Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ Z-–Ї—А–Є—В–µ—А–Є—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ
–Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ Z-–Ї—А–Є—В–µ—А–Є—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ
 ,
,
–≥–і–µ  –µ—Б—В—М —Б—А–µ–і–љ–µ–µ –њ—А–Є –љ—Г–ї–µ–≤–Њ–є –≥–Є–њ–Њ—В–µ–Ј–µ,
–µ—Б—В—М —Б—А–µ–і–љ–µ–µ –њ—А–Є –љ—Г–ї–µ–≤–Њ–є –≥–Є–њ–Њ—В–µ–Ј–µ,  вАФ —Б—А–µ–і–љ–µ–µ –њ—А–Є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј–µ,
вАФ —Б—А–µ–і–љ–µ–µ –њ—А–Є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј–µ,  вАФ –≤–µ–ї–Є—З–Є–љ–∞ –Ї—А–Є—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П Z-—Б—В–∞—В–Є—Б—В–Є–Ї–Є –њ—А–Є –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–Љ Z-—В–µ—Б—В–µ, –Є
вАФ –≤–µ–ї–Є—З–Є–љ–∞ –Ї—А–Є—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П Z-—Б—В–∞—В–Є—Б—В–Є–Ї–Є –њ—А–Є –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–Љ Z-—В–µ—Б—В–µ, –Є  вАФ —Б—В–∞–љ–і–∞—А—В–љ–∞—П –Њ—И–Є–±–Ї–∞.
вАФ —Б—В–∞–љ–і–∞—А—В–љ–∞—П –Њ—И–Є–±–Ї–∞.
–Т–µ–ї–Є—З–Є–љ–∞ —Н—Д—Д–µ–Ї—В–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–µ—А—И–µ–љ–Є—П –Њ—И–Є–±–Ї–Є –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞. –Ъ–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –≤–µ–ї–Є—З–Є–љ—Л —Н—Д—Д–µ–Ї—В–∞ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –Љ–µ—А–Њ–є —Н—Д—Д–µ–Ї—В–∞  . –С—Л–ї –≤–≤–µ–і—С–љ –≤ —Г–њ–Њ—В—А–µ–±–ї–µ–љ–Є–µ –Ф–ґ. –Ъ–Њ—Н–љ–Њ–Љ –Є –≤—Л—З–Є—Б–ї—П–µ—В—Б—П –Ї–∞–Ї –Њ—В–љ–Њ—И–µ–љ–Є—П —А–∞–Ј–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б—А–∞–≤–љ–Є–≤–∞–µ–Љ—Л–Љ–Є —Б—А–µ–і–љ–Є–Љ–Є –Ї —Б—В–∞–љ–і–∞—А—В–љ–Њ–Љ—Г –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—О
. –С—Л–ї –≤–≤–µ–і—С–љ –≤ —Г–њ–Њ—В—А–µ–±–ї–µ–љ–Є–µ –Ф–ґ. –Ъ–Њ—Н–љ–Њ–Љ –Є –≤—Л—З–Є—Б–ї—П–µ—В—Б—П –Ї–∞–Ї –Њ—В–љ–Њ—И–µ–љ–Є—П —А–∞–Ј–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б—А–∞–≤–љ–Є–≤–∞–µ–Љ—Л–Љ–Є —Б—А–µ–і–љ–Є–Љ–Є –Ї —Б—В–∞–љ–і–∞—А—В–љ–Њ–Љ—Г –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—О
 .
.
–†–∞–Ј–Љ–µ—А –≤—Л–±–Њ—А–Ї–Є, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ–є –і–ї—П –њ–Њ–і—В–≤–µ—А–ґ–і–µ–љ–Є—П —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л, –≤–ї–Є—П–µ—В –љ–∞ —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї—Г—О –Љ–Њ—Й–љ–Њ—Б—В—М, —В–∞–Ї –Ї–∞–Ї —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ –≤—Л–±–Њ—А–Ї–Є —Г–Љ–µ–љ—М—И–∞–µ—В—Б—П —Б—В–∞–љ–і–∞—А—В–љ–∞—П –Њ—И–Є–±–Ї–∞, –∞ —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П –Љ–Њ—Й–љ–Њ—Б—В—М.
–°–Љ. —В–∞–Ї–ґ–µ
–Ы–Є—В–µ—А–∞—В—Г—А–∞
- –Ъ–µ–љ–і–∞–ї–ї –Ь., –°—В—М—О–∞—А—В –Р. –°—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Є–µ –≤—Л–≤–Њ–і—Л –Є —Б–≤—П–Ј–Є. вАФ –Ь.: –Э–∞—Г–Ї–∞, 1973.
- Hays, W. Statistics (5th ed.). Cengage Learning, 1994.