Valuare (algebră)
|
Read other articles:

ЛюсіLucy Країна Франція Регіон Гранд-Ест Департамент Мозель Округ Саррбур-Шато-Сален Кантон Дельм Код INSEE 57424 Поштові індекси 57590 Координати 48°56′33″ пн. ш. 6°28′15″ сх. д.H G O Висота 228 - 315 м.н.р.м. Площа 7,36 км² Населення 235 (01-2020[1]) Густота 28,4 ос./км² Розмі

Ein FW3/22 Pillbox-Bunker nahe dem Kennet-und-Avon-Kanal Die General Headquarters Line (auch als GHQ Line bezeichnet) war eine britische, während des Zweiten Weltkrieges angelegte Verteidigungslinie. Diese als Hauptverteidigungsstellung angelegte Linie sollte den Großraum London und das mittelenglische Industriegebiet schützen. Dieses Verteidigungssystem beginnt am Nordende der Taunton Stop Line nahe dem Ort Highbridge in Somerset, verläuft dann längs des Flusses Brue und des Kennet-und-...

A variation of Cartoon Network's current logo, which resembles the network's original logo, used since 2010. This is a list of television programs currently or formerly broadcast by Cartoon Network in the United States. The network was launched on October 1, 1992, and airs mainly animated programming, ranging from action to animated comedy. In its early years, Cartoon Network's programming was predominantly made up of reruns of Looney Tunes, Tom and Jerry, and Hanna-Barbera shows (most notabl...

1985 studio album by StarshipKnee Deep in the HooplaStudio album by StarshipReleasedSeptember 10, 1985Recorded1984−1985Studio Record Plant, Sausalito Music Grinder, Los Angeles GenreAOR, pop rockLength40:28LabelGrunt/RCAProducer Peter Wolf Jeremy Smith Dennis Lambert (executive producer) Starship chronology Knee Deep in the Hoopla(1985) No Protection(1987) Singles from Knee Deep in the Hoopla We Built This CityReleased: August 1985 (US)[1] SaraReleased: December 1985 Tomorro...

2022 Indian crime thriller web series A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (July 2022) (Learn how and when to remove this template message) Cyber Vaar – Har Screen Crime Scene is and Indian crime thriller web series directed by Ankush Bhatt. Produced by Tanveer Bookwala under the banner of Ding En...

『聖カタリナの神秘の結婚』英語: Mystic Marriage of St. Catherine作者ハンス・メムリンク製作年1480年代初期寸法67 cm × 72.1 cm (26 in × 28.4 in)所蔵メトロポリタン美術館、ニューヨークウェブサイトハンス・メムリンク『聖カタリナの神秘の結婚』 (英語) 『聖カタリナの神秘の結婚』(せいカタリナのしんぴのけっこん、英: Mystic Marriage of St. Cath...

Carthusian monastery in Galluzzo, Florence Florence Charterhouse church The courtyard of the monastery Florence Charterhouse (Certosa di Firenze or Certosa del Galluzzo) is a charterhouse, or Carthusian monastery, located in the Florence suburb of Galluzzo, in central Italy. The building is a walled complex located on Monte Acuto, at the point of confluence of the Ema and Greve rivers. The charterhouse was founded in 1341 by the Florentine noble Niccolò Acciaioli, Grand Seneschal of the King...
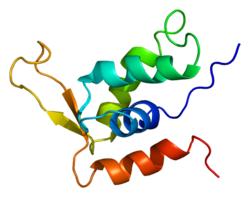
Protein-coding gene in the species Homo sapiens FOXK2Available structuresPDBOrtholog search: PDBe RCSB List of PDB id codes1JXS, 2C6YIdentifiersAliasesFOXK2, ILF, ILF-1, ILF1, forkhead box K2, nGTBPExternal IDsOMIM: 147685 MGI: 1916087 HomoloGene: 18748 GeneCards: FOXK2 Gene location (Human)Chr.Chromosome 17 (human)[1]Band17q25.3Start82,519,713 bp[1]End82,644,662 bp[1]Gene location (Mouse)Chr.Chromosome 11 (mouse)[2]Band11|11 E2Start121,259,990 bp[2 ...

American judge Denning's portrait at the Illinois Supreme Court. William A. Denning (1817 – September 4, 1856) was an American jurist and politician. Born in Kentucky, Denning moved to Frankfort, Illinois to practiced law. He then moved to Benton, Illinois when the county seat for Franklin County, Illinois was relocated from Frankfort to Benton. From 1844 to 1847, Denning served in the Illinois House of Representatives and was a Democrat. From 1847 to 1848, Denning served on the Illinoi...

このページのノートに、このページに関する注意があります。(2021年10月)注意の要約:過去の報道について この記事の主題はウィキペディアにおける独立記事作成の目安を満たしていないおそれがあります。目安に適合することを証明するために、記事の主題についての信頼できる二次資料を求めています。なお、適合することが証明できない場合には、記事は統合�...

Non-profit civil rights organization This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (May 2020) (Learn how and when to remove this template message) This art...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2019) ديك يونغ معلومات شخصية تاريخ الميلاد 16 سبتمبر 1885 تاريخ الوفاة 1 يوليو 1968 (82 سنة) الجنسية المملكة المتحدة المملكة المتحدة لبريطانيا العظمى وأيرلندا (–...

Device inserted into the vagina for medical purposes This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Pessary – news · newspapers · books · scholar · JSTOR (May 2008) (Learn how and when to remove this template message) Gold-plated stem pessary (intrauterine device) from 1920 A pessary is a prosthetic device ...

South Korean actor and singer For the football player, see Lee Jun-ki. In this Korean name, the family name is Lee. Lee Joon-giLee in 2022Born (1982-04-17) 17 April 1982 (age 41)Busan, South KoreaEducationSeoul Arts CollegeOccupationsActorsingerdancermodelYears active2001–presentAgentNamoo Actors[1]Korean nameHangul이준기Hanja李準基Revised RomanizationI Jun-giMcCune–ReischauerYi Chungi Websitewww.leejoongi.co.kr Lee Joon-gi (born 17 April 1982)[2] is a Sout...

The Lion Arts Centre in Adelaide's West End at night. The venue has hosted live music since 1986. Music of Adelaide includes music relating to the city of Adelaide, South Australia. It includes all genres of both live and recorded music by artists born or living in the city, live music events happening in the city, and other aspects of the music industry relating to Adelaide. Adelaide is a UNESCO City of Music. It enjoys several annual music festivals and awards, and possibly has more live mu...

У этого термина существуют и другие значения, см. Дом Союзов (значения). ДостопримечательностьДом Союзов Фасад со стороны Охотного Ряда 55°45′31″ с. ш. 37°36′59″ в. д.HGЯO Страна Россия Город Москва, ЦАО, Тверской район, ул. Большая Дмитровка, д. 1 Архитектурный стил�...

Chemical compound PrulifloxacinClinical dataTrade namesQuisnon, Unidrox, Prixina, GlimbaxAHFS/Drugs.comInternational Drug NamesRoutes ofadministrationOralATC codeJ01MA17 (WHO) Legal statusLegal status Rx-only (Japan, Italy, Austria) Pharmacokinetic dataMetabolismBy esterases, to ulifloxacinElimination half-life7.7 to 8.9 hoursExcretionRenal and fecalIdentifiers IUPAC name (RS)-6-Fluoro-1-methyl-7-[4-(5-methyl-2-oxo-1,3-dioxolen-4-yl)methyl-1-piperazinyl]-4-oxo-4H-[1,3]thiazeto[3,2-a...

Stefanía Serie de televisiónGénero TelenovelaCreado por Alfredo LimaBasado en My Cousin Rachelde Daphne du Maurier.Guion por Historia OriginalAlfredo LimaAdaptaciónGerardo GalvánDirigido por Martha RegueraProtagonistas Silvia MontanariAlberto MartínJorge BarreiroCristina TejedorTema principal Mi gran necesidad(interpretado por María Celeste)Ambientación Mar del Plata, 1981País de origen ArgentinaIdioma(s) original(es) EspañolN.º de episodios 129LanzamientoMedio de difusión Canal 1...

Ned BeattyDate personaleNăscut6 iulie 1937[1][2][3][4] Louisville, Kentucky, SUA[5] Decedat13 iunie 2021 (83 de ani)[6][7] Los Angeles, California, SUA[6][7] Cauza decesuluicauze naturale[6][7] Număr de copii8 Cetățenie Statele Unite ale Americii Ocupațieumoristactor de filmactor de televiziune[*]actor de voce[*]actor de teatru[*]actor Limbi vorbitelimba engleză[8] A...

Cees Heerschop Personlig informationFulde navn Cees HeerschopFødt 14. februar 1935(1935-02-14) Hilversum, HollandDød 24. juli 2014 (79 år)Eindhoven, TysklandHøjde 178 cm.Position ForsvarerSeniorkarriere*År Hold Kampe† (Mål)†1956–1964 PSV 191 (1)1964–1965 NEC 10 (1) * Seniorklubkampe og -mål tælles kun for den hjemlige liga. † Kampe (mål). Cees Heerschop (14. februar 1935 - 24. juli 2014) var en hollandsk fodboldspiller (forsvarer). Han spillede i Æresdivisionen f...
























