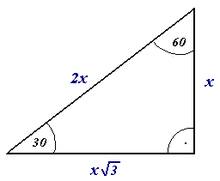
Ângulo reto
|
Read other articles:

Political party in Spain Revolutionary Anticapitalist Left Izquierda Anticapitalista RevolucionariaFounded2015Split fromAnticapitalistasNewspaperRevista IZAR[1]IdeologyTrotskyismRevolutionary socialismInternationalismPolitical positionFar-leftNational affiliationNo Hay Tiempo Que Perder Iniciative[2]Websiteizar-revolucion.orgPolitics of SpainPolitical partiesElections Revolutionary Anticapitalist Left (Spanish: Izquierda Anticapitalista Revolucionaria, IZAR) is a...

六部興行(ろくぶこうぎょう)とは、東宝株式会社の傍系の興行会社である北海道東宝株式会社、東宝東部興行株式会社(後の東宝東日本興行株式会社)、東宝関東興行株式会社(後に東宝東日本興行株式会社に合併)、中部興行株式会社(後の中部東宝株式会社)、東宝関西興行株式会社、東宝九州興行株式会社(後の九州東宝株式会社)の6社の総称である。現在は北

فورينالعلمشعار النبالةالتسميةمواقع الويب voeren.be (الهولندية)fourons.be (الفرنسية) تقسيم إداريالبلد بلجيكا التقسيم الأعلى Arrondissement of Tongeren (en) العاصمة 's-Gravenvoeren (en) خصائص جغرافيةالمساحة 50٫63 كم² الارتفاع 128 م[1] السكانعدد السكان 4٬160[2] (2018) تسمية السكان Voerenaar (بالهولندية) معلومات...

Орден преподобних Антонія і Феодосія Печерських I ступінь II ступінь Країна УкраїнаТип ОрденВручається: Предстоятелям Помісних Церков, главам держав, єпископату, вищим державним та посадовим особамПідстава за особисті заслуги у справі розвитку та зміцнення міжцерков

Hochheim Landgemeinde Nessetal Koordinaten: 51° 1′ N, 10° 40′ O51.01694444444410.659166666667277Koordinaten: 51° 1′ 1″ N, 10° 39′ 33″ O Höhe: 277 m Fläche: 7,67 km² Einwohner: 446 (31. Dez. 2017) Bevölkerungsdichte: 58 Einwohner/km² Eingemeindung: 1. Januar 2019 Postleitzahl: 99869 Vorwahl: 036255 Die restaurierte St.-Nikolaus-Kirche und der neu gestaltete Dorfplatz von HochheimDie restaurierte St....

Olympiasieger Rudern Übersicht Medaillengewinner Medaillengewinnerinnen Die erfolgreichsten Teilnehmer Nationenwertungen Die Sportart Rudern wird bei den Olympischen Spielen seit 1900 ausgetragen. Der Wettbewerb wird als olympische Ruderregatta bezeichnet und ist der sportlich anspruchsvollste und angesehenste Wettkampf im internationalen Rudersport. Bei den ersten Olympischen Spielen der Neuzeit im Jahr 1896 mussten die Ruderwettkämpfe aufgrund starker Winde ausfallen.[1] Von 1900 ...

NHL 2005/06 Liga National Hockey League Zeitraum 5. Oktober 2005 bis 19. Juni 2006 Teams 30 Spiele/Team 82 Draft Austragung NHL Entry Draft 2005 Top-Pick Kanada Sidney Crosby Gewählt von Pittsburgh Penguins Reguläre Saison Presidents’ Trophy Detroit Red Wings MVP Kanada Joe Thornton (Boston & San Jose) Topscorer Kanada Joe Thornton (Boston & San Jose) Playoffs Stanley-Cup-Sieger Carolina Hurricanes Finalist Edmonton Oilers Playoff-MVP Kanada Cam Ward (Carolina) NHL-Saisons ◄ vor...

Railway station in Saiki, Ōita Prefecture, Japan Saiki Station佐伯駅Saiki Station in 2020General informationLocation6 Hiranomachi, Saiki-shi, Ōita-ken 876-0805JapanCoordinates32°58′20.63″N 131°54′6.53″E / 32.9723972°N 131.9018139°E / 32.9723972; 131.9018139Operated by JR KyushuLine(s)■ Nippō Main LineDistance197.8 km from KokuraPlatforms1 side + 1 island platformTracks3 + multiple sidingsConstructionStructure typeAt gradeAccessibleNo - platforms lin...

For the stadium previously known as Liberty Bowl Memorial Stadium and where the game is held, see Simmons Bank Liberty Stadium. Annual American college football postseason game Liberty Bowl AutoZone Liberty Bowl StadiumSimmons Bank Liberty StadiumLocationMemphis, TennesseePrevious stadiumsPhiladelphia Municipal Stadium (1959–1963)Convention Hall (1964)Previous locationsPhiladelphia (1959–1963)Atlantic City, New Jersey (1964)Operated1959–presentConference tie-insBig 12 #4 Pick[1]...

الإمبراطورية الرومانية الغربية Senatus Populusque Romanus (اللاتينية)Imperium Romanum الإمبراطورية الرومانية القسم الغربي من الإمبراطورية الرومانية 285 – 476 ↓ الإمبراطورية الرومانية الغربيةعلم الإمبراطورية الرومانية الغربيةشعار الإمبراطورية الرومانية الغربية في أقصى اتساع لها في 395...

1967 film Don't Sting the MosquitoDirected byLina WertmüllerWritten byLina WertmüllerCinematographyDario Di PalmaEdited byFranco FraticelliMusic byBruno CanforaRelease date 24 March 1967 (1967-03-24) LanguageItalian Don't Sting the Mosquito (Italian: Non stuzzicate la zanzara) is a 1967 Italian musicarello film directed by Lina Wertmüller (under the stage name George H. Brown). It is the sequel of Rita the Mosquito.[1][2] Cast Rita Pavone: Rita Santangelo Gia...

Game of chess via postal system or e-mail This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2020) (Learn how and when to remove this template message) Postcard for international correspondence chess Correspondence chess is chess played by various forms of long-distance correspondence, traditionally through the postal system. Today it is usually played t...

Keuskupan CórdobaDioecesis Cordubensis in MexicoDiócesis de CórdobaKatolik Catedral de la Inmaculada ConcepciónLokasiNegara MeksikoProvinsi gerejawiProvinsi JalapaStatistikLuas1.627 sq mi (4.210 km2)Populasi- Total- Katolik(per 2006)707.542650,938 (92%)Paroki39InformasiDenominasiKatolik RomaRitusRitus RomaPendirian15 April 2000 (23 tahun lalu)KatedralKatedral Dikandung Tanpa NodaKepemimpinan kiniPausFransiskusUskupEduardo Cirilo Carmona Ortega, C.O....

Catholic bishop The Most ReverendChristopher Edward ByrneBishop of GalvestonChurchRoman Catholic ChurchSeeDiocese of GalvestonAppointedJuly 18, 1918InstalledNovember 10, 1918Term endedApril 1, 1950PredecessorNicolaus Aloysius GallagherSuccessorWendelin Joseph NoldOrdersOrdinationSeptember 23, 1891by Archbishop Peter Richard KenrickConsecrationNovember 10, 1919by Archbishop John J. GlennonPersonal detailsBorn(1867-04-21)April 21, 1867Byrnesville, MissouriDiedApril 1, 1950(1950-04-01)...

Insects au gratin by Susana Soares Dear Future by Sita Kuratomi Bhaumik Concept of Life by Piet Hecker and Karel Goudsblom Rusty Knives by Revital Cohen and Tuur van Balen The World Food Festival was held from 18 September to 27 October 2013 in Rotterdam. The festival took place from Rotterdam's Museumpark out over the city and harbor. It was held for more than five weeks with shows and talks by caterers, food producers, chefs and scientists.[1] The port town of Rotterdam hosted the E...

Former prison in Shrewsbury, Shropshire, United Kingdom Shrewsbury PrisonMain entrance to Shrewsbury PrisonLocationShrewsbury, ShropshireStatusOpen to the publicSecurity classAdult Male/Category B&COpened1877/1878Closed2013Managed byThe Campbell GroupGovernorGerry HendryWebsitehttps://www.shrewsburyprison.com Inside A Wing at Shrewsbury Prison HM Prison Shrewsbury was a Category B/C men's prison in Shrewsbury, Shropshire, England. It was decommissioned in March 2013, and is now open to th...

Премія Чарлза Старка Дрейпераангл. Charles Stark Draper Prize Країна СШАТип наукова нагородаdВручає: Національна інженерна академія США На честь: Чарлз Старк Дрейпер Нагородження Засновано: 1989Нагороджені: Категорія:Лауреати премії Дрейпера (50)Черговість Сайт nae.edu/55291/DraperWinn...

For other uses, see Aladdin (disambiguation). 1939 American filmAladdin and His Wonderful LampTitle screenDirected byDave FleischerStory byBill Turner (uncredited)Jack Ward (uncredited)Cal Howard (uncredited)Izzy Sparber (uncredited)Produced byMax FleischerStarringMargie HinesJack MercerCarl MeyerArthur BoranMusic bySammy TimbergAnimation byDavid TendlarNicholas TafuriWilliam SturmReuben GrossmanColor processTechnicolorProductioncompanyFleischer StudiosDistributed byParamount PicturesRelease ...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Rothschild Fellowship – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this template message) AwardRothschild FellowshipAwarded forExcellence in their field(s)CountryIsraelPresented byYad Hanadiv (The Rothschild Foundation)First awarded1979; 44 years ago&#...

En física, el espacio es una entidad geométrica en la que interactúan los objetos físicos y en el que los sucesos que ocurren tienen una posición y dirección.[1] El espacio físico es habitualmente concebido con tres dimensiones lineales, aunque los físicos modernos usualmente lo consideran, junto con el tiempo, como una parte de un continuo de cuatro dimensiones conocido como espacio-tiempo, que en presencia de materia es curvo. En matemáticas se examinan espacios con diferent...