Lista de momentos de inércia

O momento de inércia de massa, chamado aqui de ${\displaystyle I}$, mede o grau em que um objecto resiste aceleração de rotação em torno de um eixo, e é o análogo à massa para rotação. Momentos de inércia têm unidades de dimensão: massa × comprimento ². Ela não deve ser confundido com o momento de inércia utilizado no cálculo de flexão, que é uma unidade de área. Objectos geometricamente simples têm momentos de inércia que podem ser expressas em uma formula matemática com propriedades geométricas, mas isso pode não ser possível em objetos com geometria mais complexas.

Os momentos de inércia a seguir assumem densidade homogênea e o eixo de rotação passa pelo centro de massa, a menos que especificado de outra forma.

Momentos de Inércia

Descrição	Figura	Momento(s) de inércia	Comentários
Massa pontual m a uma distância r dos eixos de rotação.		${\displaystyle I=mr^{2}}$	Um ponto de massa não tem um momento de inércia em torno de seu próprio eixo, mas usando o teorema dos eixos paralelos um momento de inércia em torno de um eixo de rotação é distante alcançado.
Duas massas pontuais, M e m, com a massa reduzida ${\displaystyle \mu }$ e separadas por uma distância x.		${\displaystyle I={\frac {Mm}{M\!+\!m}}x^{2}=\mu x^{2}}$	—
Barra de comprimento L e massa m (Eixo de rotação no fim da barra)		${\displaystyle I_{\mathrm {fim} }={\frac {mL^{2}}{3}}\,\!}$  [1]	Esta expressão assume que a haste é um fio infinitamente fino (mas rígida). Este também é um caso especial da placa rectangular fina com o eixo de rotação ao final da placa, com h = L e w = 0.
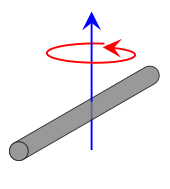
Barra de comprimento L e massa m		${\displaystyle I_{\mathrm {centro} }={\frac {mL^{2}}{12}}\,\!}$  [1]	Esta expressão assume que a haste é um fio infinitamente fino (mas rígida). Este é um caso especial da placa rectangular fina com o eixo de rotação no centro do prato, com w = L e h = 0.
Aro circular de raio r e massa m		${\displaystyle I_{z}=mr^{2}\!}$ ${\displaystyle I_{x}=I_{y}={\frac {mr^{2}}{2}}\,\!}$	Este é um caso especial de um toro com b = 0 (ver abaixo) ou de um tubo cilíndrico de paredes espessas, com as extremidades abertas com r1 = r2 e h = 0.
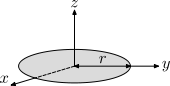
Disco fino de raio r e massa m		${\displaystyle I_{z}={\frac {mr^{2}}{2}}\,\!}$ ${\displaystyle I_{x}=I_{y}={\frac {mr^{2}}{4}}\,\!}$	Este é um caso especial do cilíndro sólido com h = 0. Os momentos ${\displaystyle I_{x}=I_{y}={\frac {I_{z}}{2}}\,}$ são consequência do teorema dos eixos perpendiculares.
Casca cilíndrica fina com as extremidades abertas, de raio r e massa m		${\displaystyle I=mr^{2}\,\!}$  [1]	Esta expressão assume a espessura da casca é insignificante. É um caso especial do tubo cilíndrico de paredes espessas para r1 = r2. Além disso, um ponto de massa (m) na extremidade de uma barra de comprimento r tem neste mesmo momento de inércia e a quantidade r é chamado o raio de rotação.
Cilíndro sólido de raio r, altura h e massa m		${\displaystyle I_{z}={\frac {mr^{2}}{2}}\,\!}$  [1] ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)}$	Este é um caso especial do tubo cilíndrico de paredes espessas, com r1 = 0. (Note: eixo X-Y deve ser trocado por uma referência que segue a regra da mão direita.)
Tubo cilíndrico de paredes espessas com extremidades abertas, raio interno r1, raio externo r2, comprimento h e massa m		${\displaystyle I_{z}={\frac {1}{2}}m\left({r_{2}}^{2}+{r_{1}}^{2}\right)}$  [1][2] ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{2}}^{2}+{r_{1}}^{2}\right)+h^{2}\right]}$ ou quando a espessura normal tn é definida = t/r e deixando r = r2, então ${\displaystyle I_{z}=mr^{2}\left(1-t_{n}+{\frac {1}{2}}{t_{n}}^{2}\right)}$	Com a densidade ρ e a mesma geometria ${\displaystyle I_{z}={\frac {1}{2}}\pi \rho h\left({r_{2}}^{4}-{r_{1}}^{4}\right)}$ ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}\pi \rho h\left(3({r_{2}}^{4}-{r_{1}}^{4})+h^{2}({r_{2}}^{2}-{r_{1}}^{2})\right)}$
Tetraedro de lado s e massa m		${\displaystyle I_{solid}={\frac {3ms^{2}}{7}}\,\!}$ ${\displaystyle I_{hollow}={\frac {4ms^{2}}{7}}\,\!}$	—
Octaedro (oco) de lado s e massa m		${\displaystyle I_{z}=I_{x}=I_{y}={\frac {5ms^{2}}{9}}\,\!}$	—
Octaedro (sólido) de lado s e massa m		${\displaystyle I_{z}=I_{x}=I_{y}={\frac {ms^{2}}{6}}\,\!}$	—
Esfera (oca) de raio r e massa m		${\displaystyle I={\frac {2mr^{2}}{3}}\,\!}$  [1]	Uma esfera oca pode ser definida por dois aros circulares infinitamente finos, em que o raio varia de 0 a r (ou por um único aro cujo raio varia de -r a r).
Bola (sólida) de raio r e massa m		${\displaystyle I={\frac {2mr^{2}}{5}}\,\!}$  [1]	Uma esfera oca pode ser definida por dois aros circulares infinitamente finos, em que o raio varia de 0 a r (ou por um único aro cujo raio varia de -r a r). Ela também pode ser definida por esferas ocas, infinitamente finas, cujo raio varia de 0 a r.
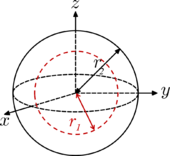
Esfera (casca) de raio r2, com cavidade cocentrica de raio r1 e massa m		${\displaystyle I={\frac {2m}{5}}\left[{\frac {{r_{2}}^{5}-{r_{1}}^{5}}{{r_{2}}^{3}-{r_{1}}^{3}}}\right]\,\!}$  [1]	Quando a cavidade central tiver raio r1 = 0, o objeto é uma bola sólida (ver acima). Se r1 = r2, ${\displaystyle \left[{\frac {{r_{2}}^{5}-{r_{1}}^{5}}{{r_{2}}^{3}-{r_{1}}^{3}}}\right]={\frac {5}{3}}{r_{2}}^{2}}$ , o objeto é uma esfera oca.
Cone circular de raio r, altura h e massa m		${\displaystyle I_{z}={\frac {3}{10}}mr^{2}\,\!}$  [3] ${\displaystyle I_{x}=I_{y}={\frac {3}{5}}m\left({\frac {r^{2}}{4}}+h^{2}\right)\,\!}$  [3]	—
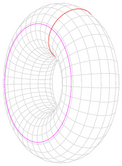
Toro de um tubo de raio a, raio da seção transversal b e massa m.		Sobre um eixo do plano diametral: ${\displaystyle {\frac {1}{8}}\left(4a^{2}+5b^{2}\right)m}$  [4] Sobre o eixo vertical: ${\displaystyle \left(a^{2}+{\frac {3}{4}}b^{2}\right)m}$  [4]	—
Elipsoide (sólido) de semieixos a, b e c com eixo de rotação em a e massa m		${\displaystyle I_{a}={\frac {m(b^{2}+c^{2})}{5}}\,\!}$ ${\displaystyle I_{b}={\frac {m(a^{2}+c^{2})}{5}}\,\!}$ ${\displaystyle I_{c}={\frac {m(a^{2}+b^{2})}{5}}\,\!}$	—
Placa retangular fina de altura h, espessura w e massa m (Eixo de rotação no fim da placa)		${\displaystyle I_{e}={\frac {mh^{2}}{3}}+{\frac {mw^{2}}{12}}\,\!}$	—
Placa retangular fina de altura h, espessura w e massa m		${\displaystyle I_{c}={\frac {m(h^{2}+w^{2})}{12}}\,\!}$  [1]	—
Cuboide sólido de altura h, espessura w, profundidade d e massa m		${\displaystyle I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)}$ ${\displaystyle I_{w}={\frac {1}{12}}m\left(h^{2}+d^{2}\right)}$ ${\displaystyle I_{d}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)}$	Para cubo com mesma orientação e lados de comprimento ${\displaystyle s}$, ${\displaystyle I_{CM}={\frac {ms^{2}}{6}}\,\!}$.
Cuboide sólido de altura D, espessura W, comprimento L e massa m com sua diagonal mais longa como eixo de rotação.		${\displaystyle I={\frac {m\left(W^{2}D^{2}+L^{2}D^{2}+L^{2}W^{2}\right)}{6\left(L^{2}+W^{2}+D^{2}\right)}}}$	Para um cubo de lados ${\displaystyle s}$, ${\displaystyle I={\frac {ms^{2}}{6}}\,\!}$.
Polígono plano de vértices ${\displaystyle {\vec {P}}_{1}}$, ${\displaystyle {\vec {P}}_{2}}$, ${\displaystyle {\vec {P}}_{3}}$, ..., ${\displaystyle {\vec {P}}_{N}}$ e massa ${\displaystyle m}$, girando em torno de um eixo perpendicular ao plano e passando pela origem.		${\displaystyle I={\frac {m}{6}}{\frac {\sum \limits _{n=1}^{N-1}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|(({\vec {P}}_{n+1}\cdot {\vec {P}}_{n+1})+({\vec {P}}_{n+1}\cdot {\vec {P}}_{n})+({\vec {P}}_{n}\cdot {\vec {P}}_{n}))}{\sum \limits _{n=1}^{N-1}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|}}}$	Esta expressão assume que o polígono tem forma de estrela. Os vetores ${\displaystyle {\vec {P}}_{1}}$, ${\displaystyle {\vec {P}}_{2}}$, ${\displaystyle {\vec {P}}_{3}}$, ..., ${\displaystyle {\vec {P}}_{N}}$ são vectores posição dos vértices.
Disco infinito de massa normalmente distribuída ao longo do plano perpendicular ao eixo de rotação (i.e. ${\displaystyle \rho (x,y)={\tfrac {m}{2\pi ab}}\,e^{-((x/a)^{2}+(y/b)^{2})/2}}$ Onde: ${\displaystyle \rho (x,y)}$ é a função densidade de massa).		${\displaystyle I=m(a^{2}+b^{2})\,\!}$	—

Referências

1. Raymond A. Serway (1986). Physics for Scientists and Engineers, second ed. [S.l.]: Saunders College Publishing. p. 202. ISBN 0-03-004534-7 
2. Classical Mechanics - Moment of inertia of a uniform hollow cylinder. LivePhysics.com. Retrieved on 2008-01-31.
3. Ferdinand P. Beer and E. Russell Johnston, Jr (1984). Vector Mechanics for Engineers, fourth ed. [S.l.]: McGraw-Hill. p. 911. ISBN 0-07-004389-2 
4. Eric W. Weisstein. «Moment of Inertia — Ring». Wolfram Research. Consultado em 25 de março de 2010