Equação de Lane-Emden
|
Read other articles:

Chlorophytum amaniense Klasifikasi ilmiah Superdivisi: Spermatophyta Divisi: Magnoliophyta Ordo: Asparagales Famili: Asparagaceae Genus: Chlorophytum Spesies: C. amaniense Nama binomial Chlorophytum amaniense Chlorophytum amaniense, tanaman mandarin adalah sejenis tanaman laba-laba yang bisa digolongkan sebagai jenis baru di dunia tanaman hias. Tanaman ini pertama kali dibawa ke Amerika Utara pada tahun 1990-an dan popularitasnya terus meningkat, karena tanaman ini memiliki warna yang me...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أغسطس 2017) تم إستكشاف نظرية الأساس البيولوجي للحب بواسطة العلوم البيولوجية مثل علم النفس التطوري، وعلم الأحياء التطوري، والأنثروبولوجيا، وعلم الأعصاب. وقد تم دراسة ا�...

Wappen Sachsen-Anhalts Details Zum Führen des Wappens berechtigt Sachsen-Anhalt, den Behörden und sonstigen Stellen des Landes vorbehalten[1] Eingeführt 29. Januar 1991 Das Wappen Sachsen-Anhalts ist neben der Landesflagge, der Landesdienstflagge und dem Landessiegel eines der Hoheitszeichen des Landes Sachsen-Anhalt.[1] Es wurde durch das Gesetz über Wappen, Flaggen und Siegel am 29. Januar 1991 eingeführt.[2] Inhaltsverzeichnis 1 Wappenbeschreibung 2 Bedeutung 3...

Nakagawa中川村 VillaBanderaEscudo NakagawaLocalización de Nakagawa en Japón Nakagawa en la prefectura de NaganoCoordenadas 35°38′04″N 137°56′45″E / 35.634527777778, 137.94597222222Entidad Villa • País JPN • Región Chūbu • Isla Honshū • Prefectura Nagano • Distrito KamiinaSuperficie • Total 77,05 km²[1]Población (1 de marzo de 2021) • Total 4585 hab. • Densidad 59,51 hab/km

Macroditassa Macroditassa adnataTaxonomíaReino: PlantaeSubreino: TracheobiontaDivisión: MagnoliophytaClase: MagnoliopsidaSubclase: AsteridaeOrden: GentianalesFamilia: ApocynaceaeSubfamilia: AsclepiadoideaeTribu: AsclepiadeaeSubtribu: MetastelmatinaeGénero: MacroditassaMalmeEspecie tipo Macroditassa adnata(E. Fourn.) MalmeEspecies Ver texto [editar datos en Wikidata] Macroditassa es un género de fanerógamas de la familia Apocynaceae. Contiene 12 especies.[1] Es ori...

Foundation tablet for the temple of Nanaia, built by Kudur-Mabuk and his son Rim-Sin I, rulers of Larsa. Circa 1820 BCE. Louvre Museum. Kudur-Mabuk was a ruler in the ancient Near East city-state of Larsa from 1770 BC to 1754 BC (short chronology) or 1830s BC (middle chronology). His sons Warad-Sin (1834-1823) and Rim-Sin I (1822-1763) were kings of Larsa. His daughter En-ane-du was high priestess of the moon god in Ur. [1] [2] [3] See also Chronology of the ancient Ne...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (septembre 2022). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Si ce bandeau n'est plus pertinent, retirez-le. ...

Future MRT depot in Singapore Not to be confused with Changi Depot. Changi East DepotChangi East Depot construction site in June 2022LocationLocationChangiCharacteristicsOwnerLand Transport AuthorityTypeAt-grade/undergroundRoadsAviation Park Road, Tanah Merah Coast RoadRoutes served CRL Cross Island lineHistoryOpened2030; 7 years' time (2030) Changi East Depot is a future train depot in Changi East, Singapore. At 57 ha (140-acre), the at-grade depot will hous...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (August 2009) (Learn how and when to remove this template message) The Brussels Cross on display The Brussels Cross or Drahmal Cross is an Anglo-Saxon cross-reliquary of the early 11th century, now in the treasury of the St. Michael and St. Gudula Cathedral, Brussels, that bears engraved images and an inscription...
Rijssen-Holten, adalah sebuah gemeente Belanda yang terletak di provinsi Overijssel. Pada tahun 2006 daerah ini memiliki penduduk sebesar 36.432 jiwa. Lihat pula Daftar Kota Belanda lbsMunisipalitas di provinsi Overijssel Almelo Borne Dalfsen Deventer Dinkelland Enschede Haaksbergen Hardenberg Hellendoorn Hengelo Hof van Twente Kampen Losser Oldenzaal Olst-Wijhe Ommen Raalte Rijssen-Holten Staphorst Steenwijkerland Tubbergen Twenterand Wierden Zwartewaterland Zwolle Artikel bertopik geografi ...

الثقافة الأعلام والتراجم الجغرافيا التاريخ الرياضيات العلوم المجتمع التقانات الفلسفة الأديان فهرس البوابات هذه البوابة رياضية هناك 8٬247 مقالة مرتبطة بالبوابة أهلا بكم في بوابة سباق الدر�...
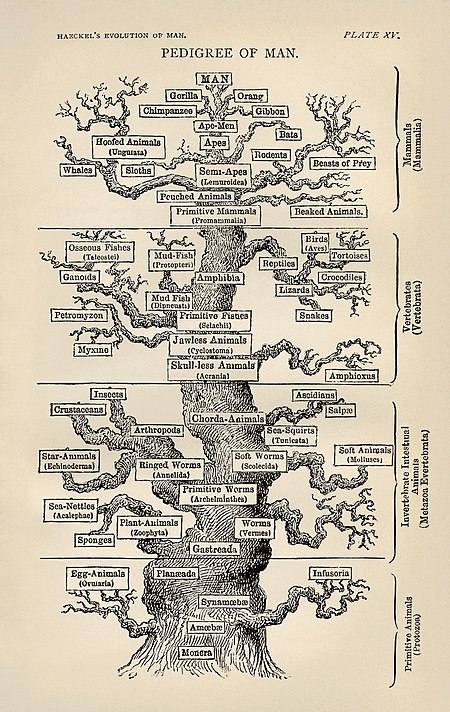
Biologi komputasi meliputi pengembangan dan aplikasi dari data-analitis dan teoretis metode, pemodelan matematika dan simulasi komputasi teknik untuk mempelajari biologi, perilaku, dan sistem sosial.. Bidang ini didefinisikan secara luas dan mencakup dasar-dasar dalam ilmu komputer, matematika, animasi, statistik, biokimia, kimia, biofisika, biologi molekuler, genetika, genetika, ekologi, evolusi, anatomi, neuroscience, dan visualisasi. Biologi komputasi berbeda dari komputasi biologi, yang m...
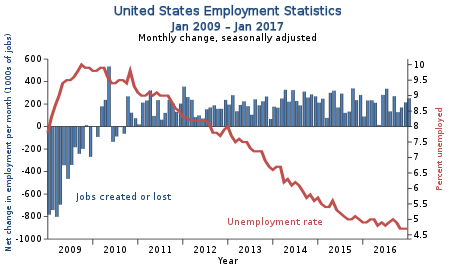
Explanation of unemployment in the United States, presently and historically This article is part of a series on theEconomy of theUnited States Economic history Agricultural history Banking history Petroleum history Shipbuilding Industrial Revolution in the United States History of the United States dollar Lumber history Tariff History United States dollar § History History by state Sectors Primary sector Agriculture Energy Petroleum Electricity Mining Fishing Forestry Water and sanitation S...

SS Tjisalak on Tanjung Priok Dock of 8,000 tons History NameTanjung Priok Dock of 8,000 tons BuilderBurgerhout Launched10 February 1923 CompletedJune 1923 Commissioned15 December 1923 DecommissionedAfter 1960 HomeportTanjung Priok General characteristics (as completed) Displacement 4,000t(empty) 12,500t(loaded)[1] Length156.40 m (513.1 ft)[2] Beam29.00 m (95.1 ft)[2] Depth of hold3.20 m (10.5 ft)(pontoon)[2] Tanjung Priok Dock of 8...

Alphonsus Liguori, whose teachings inspired the establishment of the Academy. The Pontifical Alphonsian Academy (Italian: Pontificia Accademia Alfonsiana; Latin: Pontificia Academia Alphonsiana), also commonly known as the Alphonsianum, is a pontifical institution of higher education founded in 1949 by the Redemptorists and located in Rome, Italy. Since 1960, the Academy has specialized in moral theology as a part of the Faculty of Theology of the Pontifical Lateran University.[1] In ...

Para la carrera de automovilismo del mismo nombre, véase Gran Premio de los Países Bajos. Circuito de Assen Ubicación Assen, Países BajosCoordenadas 52°57′42″N 6°31′24″E / 52.961666666667, 6.5233333333333Eventos Campeonato del Mundo de MotociclismoLongitud 4.545 kmCurvas 18Vuelta récord 1:32.500 (MotoGP) Aleix Espargaró Aprilia Racing (2022)[editar datos en Wikidata] El Gran Premio de los Países Bajos de Motociclismo, normalmente llamado Gr...

Basketball competition FIBA Europe Under-18 3x3 ChampionshipsSport3x3 basketballFounded2015No. of teams24CountryFIBA Europe membersContinentEuropeMost titlesM: seven teams (1 title)W: three teams (2 titles) The FIBA Europe Under-18 3x3 Championships (and FIBA Europe Under-17 3x3 Championships since 2021) is an under-17/under-18 3x3 basketball competition between FIBA Europe members. The event was held for the first time in Minsk, Belarus in 2015 and has been held annually ever since.[1 ...

Disambiguazione – Se stai cercando l'altro principale concorso di bellezza statunitense, vedi Miss America. Miss USA TipoConcorso di bellezza Fondazione1950 Sede centrale New York Sito web Modifica dati su Wikidata · Manuale Un momento della finale di Miss USA 2004 Miss USA è un concorso di bellezza femminile che si tiene annualmente dal 1952 e nel quale viene eletta la rappresentante statunitense per Miss Universo. La Miss Universe Organization si occupa di entrambi i concorsi, oltr...

Supercopa Paraguay Supercopa Paraguay 2023 Datos generalesDeporte FútbolSede Paraguay ParaguayFederación Asociación Paraguaya de FútbolConfederación ConmebolEquipos participantes 2Datos históricosFundación 2021Primera temporada 2021Primer campeón OlimpiaDatos estadísticosCampeón actual LibertadMás campeonatos Olimpia (1) Sportivo Ameliano (1) Libertad (1)Más finales Olimpia (2)Otros datosPatrocinador Ver lista Socio de TV Ver lista [editar datos en Wikidata] La Supercopa...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Agustus 2017. Andreas ChangLahir5 Oktober 1959 (umur 64)Singkawang, IndonesiaKebangsaan IndonesiaAlmamater Universitas Sanata Dharma (Drs) Edith Cowan University (MBA) Suami/istriJoke KusumaAnak2Situs webwww.andreas-chang.com Andreas Chang (lahir 5 Oktober...



























![{\displaystyle {\frac {d}{dr}}\left[C\gamma r^{2}\rho ^{\gamma -2}{\frac {d\rho }{dr}}\right]=4\pi Gr^{2}\rho \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97b101fcb3629ad4bc601d93129ff0f425d9e228)

![{\displaystyle {\frac {d}{dr}}\left[C(n+1)\rho _{c}^{\gamma -1}r^{2}{\frac {d\theta }{dr}}\right]=4\pi Gr^{2}\rho _{c}\theta ^{n}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebd1391bf3e44b9107f1bab370267d9048ef057d)
![{\displaystyle {\frac {1}{r^{2}}}{\frac {d}{dr}}\left[r^{2}{\frac {d\theta }{dr}}\right]={\frac {4\pi G\rho _{c}^{2-\gamma }}{C(n+1)}}\theta ^{n}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc35aa2ca18450830bf8821df9037173a0dbbf6)


![{\displaystyle {\frac {1}{r^{2}}}{\frac {d}{dr}}\left[r^{2}{\frac {d\theta }{dr}}\right]={\frac {4\pi G\rho _{c}^{2}}{(n+1)P_{c}}}\theta ^{n}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3742a1a6c094f2c681751c2cbbd7fb789c9090ad)
































![{\displaystyle {\frac {d^{2}\theta }{dx^{2}}}=A\left[x^{p}{\frac {d^{2}z}{dx^{2}}}+2px^{p-1}{\frac {dz}{dx}}+p(p-1)x^{p-2}z\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df619129875c58c87212adff4ea1c5cbbef49818)







