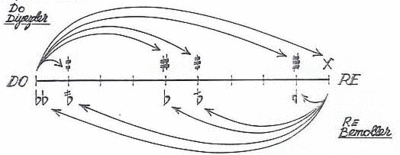
53 temperamentos iguais
|
Read other articles:

الببتيدات المضادة للميكروبات[1]: هي ببتيدات أو مجالات محددة من بروتينات، تتألف من حوالي 12- 50 حمض أميني، غالبا ما تكون غنية بالحمضين الامينيين الارجينين R، واللايزين K.[2].وهي اما ان تكون ببتيدات طبيعية تنتجها الخلية وتسمى أيضا الببتيدات الدفاعية في الخلية المضيفة، لان

Irish government from 1944 to 1948 Government of the 12th Dáil4th Government of IrelandDate formed9 June 1944Date dissolved18 February 1948People and organisationsPresidentDouglas Hyde (1944–45)Seán T. O'Kelly (1945–48)TaoiseachÉamon de ValeraTánaisteSeán T. O'Kelly (1944–45)Seán Lemass (1945–48)Total no. of members12 (1944–47)14 (1947–48)Member partyFianna FáilStatus in legislatureMajority GovernmentOpposition partyFine GaelOpposition leaderRichard MulcahyHistoryElection(s...

Masyumi beralih ke halaman ini. Untuk kegunaan lain, lihat Partai Majelis Syuro Muslimin Indonesia (disambiguasi). Partai Masyumi Partai Majelis Syuro Muslimin IndonesiaSingkatanMasyumiKetua umumSoekiman Wirjosandjojo (pertama)Mohammad NatsirPrawoto Mangkusasmito (terakhir)Dibentuk24 Oktober 1943 (organisasi) 8 November 1945 (partai)Dibubarkan17 Agustus 1960Digabungkan dariMuhammadiyah Persatuan Islam Nahdlatul Ulama Persatuan Ummat Islam Al Washliyah Al Ittihadiyah Nahdlatul Wathan Math...

Spinnerin in einer Baumwollspinnerei, 1983/85 Spinner üben das Handwerk des Spinnens als Beruf aus. Durch Ordnen, Zusammenfügen und Zwirbeln von dünnen, kurzen tierischen und pflanzlichen (Einzel-)Fasern stellten sie einen langen Faden her. Konventionelle Methoden des Spinnens mit Handspindel oder Spinnrad werden bis heute noch vor allem in verschiedenen Ländern Afrikas, Asiens und Südamerikas praktiziert. Geschichte Menschen spannen während Jahrtausenden Fäden aus Flachs, Wolle oder B...

Émile Roger Rechtsform Gründung 1888 Auflösung 1896 Sitz Paris, Frankreich Leitung Émile Roger Branche Automobilindustrie Roger-Benz von 1895 Roger-Benz Victoria (Paris–Rouen 1894, É. Roger, Nr. 85) Roger-Benz von 1895 Roger-Benz war eine französische Automarke.[1][2][3] Hersteller war Émile Roger. Inhaltsverzeichnis 1 Unternehmensgeschichte 2 Fahrzeuge 3 Literatur 4 Weblinks 5 Einzelnachweise Unternehmensgeschichte Émile Roger kaufte 1887 ein Auto von Benz. ...

Kerajaan MoreaRegno di MoreaKoloni di Republik Venesia1688–1715Peloponnesus, Kini Kerajaan Morea, oleh Frederik de Wit, 1688Ibu kotaNauplio (Napoli di Romania)SejarahPemerintahan • JenisKoloniProvveditore Generale di Morea • 1688–1690 Giacomo Corner (pertama)• 1714–1715 Alessandro Bon (terakhir) Era sejarahModern Awal• Ditaklukan oleh Venesia 1685–1687• Didirikan 1688• Ditaklukan kembali oleh Utsmaniyah 1715• Traktat Passarowi...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يناير 2017) هذه قائمة بالدول حسب عدد اللغات الرسمية المعترف بها. تتضمن القائمة الدول التي تعترف بثلاث لغات أو أكثر، سواء كانت على المستوى الوطني أو المحلي. البلد المستوى...

2000 video game This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is in list format but may read better as prose. You can help by converting this article, if appropriate. Editing help is available. (December 2011) This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all impor...

French painter (1758–1836) This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Carle Vernet – news · newspapers · books · scholar · JSTOR (March 20...

Esta é uma lista de guerras envolvendo o Egito. Egito Otomano e Quedivato do Egito (1517–1914) Conflito Combatente 1 Combatente 2 Resultados Chefe de Estado Perdasegípcias Expedição Fraser (1807) Egito Otomano Império Britânico Vitória Derrota das forças britânicas. Muhammad Ali do Egito ? Guerra Egípcio-Wahabita (1811–1818) Império Otomano Egito Otomano Diriyah Vitória Execução de Abdullah bin Saud. ~2.000[1] Guerra de independência da Grécia(1821–1829) Império O...

Региональные выборы в Пьемонте2014 годХронология2010 2019ИнформацияДата 25 мая 2014Явка 66,44 %КандидатыФотография Цвет Кандидат Серджо Кьямпарино Гильберто Пичетто Фратин[it] Давиде БоноПартия Демократическая партия Вперёд, Италия Движение пяти звёздКоалиция Левоцентрис...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. A Cunning Destiny adalah sebuah seri drama romansa Thailand tahun 2022. Seri tersebut terdiri dari 15 episode dan menampilkan Toey Pongsakorn Mettarikanon, Cheer Thikumporn Rittapinun, Marina Sadanun Balenciaga, Bright Rapheephong Thapsuwan, Tee Thanapon...

Императрица Феодора со свитой. Мозаика Сан-Витале в Равенне, 527—548 годы Византийский светский костюм — одежда, использовавшаяся светскими членами общества Византийской империи. В Византии, как и в других средневековых культурах, одежда служила средством обозначения ...

黃正銘 黄正铭(1903年10月2日—1973年5月23日),字君白,浙江省宁海县城东门人。中华民国法学家、法官。[1] 生平 黄正铭最初入柏屏学堂学习,后来入宁海县立正学高等小学堂,此后入宁波的浙江省立第四中学。毕业后,到正学小学堂担任英语教师。民国13年(1924年),考入南京国立东南大学政治系。毕业获得法学士学位。后来,参加浙江省选拔县长考试,取得第一�...

In this Spanish name, the first or paternal surname is Sánchez and the second or maternal family name is Mazas. Rafael Sánchez Mazas in 1939. Rafael Sánchez Mazas (18 February 1894 – October 1966) was a Spanish nationalist writer and a leader of the Falange, a far-right political movement created in Spain before the Spanish Civil War. Sánchez Mazas received a law degree at the Real Colegio de Estudios Superiores de María Cristina, El Escorial and in 1915 published Pequeñas mem...

Intercollegiate basketball season 2013–14 Fordham Rams women's basketball2013 Lady Rebel Round-Up Champions2013 Fordham Holiday Classic Champions2014 A10 Tournament ChampionsNCAA Women's Tournament, first roundConferenceAtlantic 10Record25–8 (11–5 A-10)Head coachStephanie Gaitley (3rd season)Assistant coaches Angelika Szumilo Dale Hodges Laura Forbes Home arenaRose Hill GymnasiumSeasons← 2012–132014–15 → 2013–14 Atlantic 10 women's basketball standi...

Washington, D.C. Wing Civil Air PatrolWashington, D.C. Wing of Civil Air PatrolAssociated branchesUnited States Air ForceCommand staffCommander Col David E. SterlingVice Commander Lt Col Aaron NewmanChief of Staff Lt Col John DaviesCurrent statisticsSquadrons7Cadets353Seniors289Total Membership642Websitenatcapwg.cap.govStatistics as of 2023vte The National Capital Wing of the Civil Air Patrol (CAP) is the highest echelon of Civil Air Patrol in the district of Washington, D.C. The National Cap...

Donkin CommandoDonkin Commando emblemCountry South AfricaAllegiance Republic of South Africa Republic of South Africa Branch South African Army South African Army TypeInfantryRoleLight InfantrySizeOne BattalionPart ofSouth African Infantry CorpsArmy Territorial Reserve, Group 6Garrison/HQDonkin, Port ElizabethMilitary unit Donkin Commando was a light infantry regiment of the South African Army. It formed part of the South African Army Infantry Formation as we...

This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) The Regalia of Romania are a set of items which were used for the coronation of the...

G.I. Joe character Fictional character ZanzibarG.I. Joe characterIllustration of Zanzibar from G.I. Joe: Order of Battle. Art by Herb Trimpe.First appearanceG.I. Joe: A Real American Hero isssue #60 (June 1987)In-universe informationAffiliationDreadnoksSpecialtyPirateFile nameMorgan TeachBirth placeCayman Islands Zanzibar is a fictional character from the G.I. Joe: A Real American Hero toyline and comic book series. He is affiliated with Cobra as the Dreadnoks' pirate and debuted in 1987. Pro...