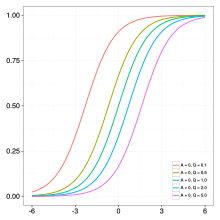
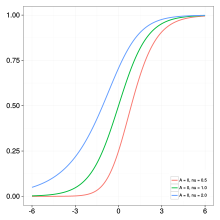
Uogólniona funkcja logistyczna
|
Read other articles:

Blanche dari PrancisMakam Blanche dari PrancisPermaisuri AustriaPeriode1300-1 Maret 1305Informasi pribadiPemakamanMinoritenkirche, ViennaWangsaIstana CapetIstana HabsburgAyahPhilip III dari PrancisIbuMaria dari Brabant, Ratu PrancisPasanganRudolph I dari Bohemia Blanche dari Prancis (tahun 1282 – 1 Maret, 1305) dilahirkan di Paris, orangtuanya adalah Philip III dari Prancis dan Maria dari Brabant, Ratu Prancis.[1] Keluarga Blanche merupakan anak kedua dari tiga anak yang dilahirkan ...

『オフィーリア』英語: Ophelia作者ジョン・エヴァレット・ミレー製作年1851年 - 1852年種類油彩、キャンバス寸法76.2 cm × 111.8 cm (30.0 in × 44.0 in)所蔵テート・ブリテン、ロンドン 『オフィーリア』(英: Ophelia)は、1851年から1852年にかけて制作されたジョン・エヴァレット・ミレーによる絵画である。 ロンドンにあるテート・ブリテン美術...

Nelson Mandela Pełne imię i nazwisko Nelson Rolihlahla Mandela Data i miejsce urodzenia 18 lipca 1918 Mvezo Data i miejsce śmierci 5 grudnia 2013 Johannesburg 8. Prezydent Republiki Południowej Afryki Okres od 10 maja 1994 do 16 czerwca 1999 Przynależność polityczna Afrykański Kongres Narodowy (ANC) Poprzednik Frederik Willem de Klerk Następca Thabo Mbeki Odznaczenia Multimedia w Wikimedia Commons Cytaty w Wikicytatach {{Polityk infobox}} Przestarzałe p...

Danau PutrajayaLetakPutrajayaJenis perairanDanau buatanTerletak di negaraMalaysia Danau Putrajaya adalah danau yang terletak di pusat kota Putrajaya, Malaysia. Danau buatan seluar 650 hektare ini dirancang sebagai sistem pendingin alami kota sekaligus fasilitas rekreasi, memancing, olahraga air, dan transportasi air. Pada tanggal 26 September 2004, F1 Powerboat Championship diadakan di danau ini untuk pertama kalinya (ketiga kalinya diadakan di Malaysia). Tahun 2005, Putrajaya menjadi tuan ru...

Pour un article plus général, voir Liste des membres du Conseil des États suisse. Cet article donne la liste des membres du Conseil des États pendant la 51e législature de l'Assemblée fédérale suisse (2019-2023)[1]. Ils sont en fonction du 2 décembre 2019 au 3 décembre 2023. Portrait Conseiller aux États Canton Parti Groupe[2] Date denaissance Conseiller aux États depuis le Profession ou titre[3] Remarques Caroni, Andrea Andrea Caroni Appenzell Rhodes-Extérieures PLR PLR 19 a...

日本の政治家鈴木 俊夫すずき としお生年月日 (1950-08-11) 1950年8月11日(73歳)出生地 日本 秋田県湯沢市出身校 岩手大学農学部農学別科畜産専攻科卒業所属政党 (日本共産党→)無所属称号 農学士旭日小綬章 湯沢市長当選回数 2回在任期間 2005年4月 - 2009年4月16日2017年4月17日 - 2021年4月16日 湯沢市長(旧)当選回数 1回在任期間 2002年 - 2005年 秋田県議会議員選挙区 旧湯沢...

Bagian dari sebuah seri tentang Muhakkimah Kepercayaan dan praktek Monoteisme Kitman Takfir Teologi Sejarah Awal Fitnah Pertama Pertempuran Siffin Pertempuran Nahrawan Dinasti Rustamiyah Nabhaniyah Ya'rubiyah Zanzibar Oman Kumpulan hadis Jami' ash-Shahih Tartib al-Musnad Tokoh terkenal Abdurrahman bin Muljam Nafi bin al-Azraq Najdah bin Amir al-Hanafi Abu Bilal Mirdas Abu Qurra Abdullah bin Ibadh Jabir bin Zayd Abu Yazid Abd Allah bin Yazid al-Fazari Cabang dan sekte Khawarij Ajardi Azariqah ...

Герб Чорнобая Герб радянського періодуДеталіНосій ЧорнобайЗатверджений 18 вересня 2002 рокуКорона міська Герб Чорнобая — офіційний символ селища міського типу Чорнобая затверджений рішенням Чорнобаївської селищної ради № 3-1 від 18 вересня 2002 року. Зміст 1 Опис 2 Поя�...

BluehostJenisSubsidiaryIndustriWeb hostingDidirikan2003; 20 tahun lalu (2003)PendiriMatt HeatonKantorpusatOrem, Utah, USTokohkunciMatt Heaton(Founder & CEO 2003–2011)Dan Handy(CEO 2011–2015)Mike Olson(CEO 2015–2016)James Grierson(CEO 2016–2017)Suhaib Zaheer(CEO 2017–2021)PemilikEndurance International GroupSitus webbluehost.comBluehost adalah perusahaan hosting web yang dimiliki oleh Endurance International Group . Itu adalah salah satu dari 20 host web terbesar pada tahun ...

Kahar TjandraInformasi pribadiLahir24 November 1929 (umur 94) Padang, Sumatera BaratAlma materUniversitas Indonesia (1998) Wamil RPKADKarier militerPihak IndonesiaDinas/cabang TNI Angkatan DaratMasa dinas1952–1967Pangkat KaptenSatuanKorps Kesehatan (Kopassus)Sunting kotak info • L • B Kapten Ckm (Purn.) dr Kahar Tjandra (Tjan Ke Hoat) (lahir 24 November 1929) merupakan seorang pengusaha dan dokter asal Indonesia. Dia adalah anak dari pasangan Hardi Sjarif (Tjan ...

Antoine Christophe MerlinEngraving by Émile Thomas on a drawing by Henri Rousseau.Lahir13 September 1762 MeninggalSeptember 1833Signature Antoine Christophe Merlin (13 September 1762 di Thionville, Moselle – September 1833 di Paris)[1] adalah seorang anggota beberapa badan legislatif pada era Revolusi Prancis. Ia biasanya disebut Merlin de Thionville (Merlin dari Thionville) untuk membedakannya dari Philippe-Antoine Merlin de Douai. Referensi ^ Chronicle of the French Revoluti...

Main article: Subprime mortgage crisis The U.S. central banking system, the Federal Reserve, in partnership with central banks around the world, took several steps to address the subprime mortgage crisis. Federal Reserve Chairman Ben Bernanke stated in early 2008: Broadly, the Federal Reserve’s response has followed two tracks: efforts to support market liquidity and functioning and the pursuit of our macroeconomic objectives through monetary policy.[1] A 2011 study by the Governmen...

Filipino TV series or program For Love or MoneyGenreDrama RomanceDeveloped byElmer L. GatchalianDirected byMac C. AlejandreStarringDerek Ramsay Ritz Azul Alice DixsonTheme music composerLara MaigueOpening themeSa 'Yo Na Lang Ako by Lara MaigueCountry of originPhilippinesOriginal languageFilipinoNo. of episodes14ProductionProduction locationsMetro Manila, PhilippinesRunning time30-45 minutesOriginal releaseNetworkTV5ReleaseOctober 17, 2013 (2013-10-17) –January 16, 2014 (...

United States warship For other ships with the same name, see USS Intrepid. A copy of an engraving of the destruction of the fire ship Intrepid History United States NameUSS Intrepid Cost$1,800 purchased Launched1798 Acquiredby capture, 23 December 1803 FateDestroyed in action, 4 September 1804 General characteristics TypeBomb ketch, used as an Explosion ship Tonnage64 Length60 ft (18 m) Beam12 ft (3.7 m) PropulsionSail Complement70 officers and enlisted Armament4 guns The...

Bilateral relationsFrance-Rwanda relations France Rwanda France–Rwanda relations are the international relations between France and Rwanda. History Early relations France and Rwanda were allies during the reign of Habyarimana.[1] Rwandan genocide See also: Role of France in the Rwandan genocide France actively supported the Hutu-led government of Juvénal Habyarimana against the Tutsi-dominated Rwandan Patriotic Front. France provided arms and military training to Habyarimana's mili...

Thousand Foot Falls, Cayo district, Belize Thousand Foot Falls is a waterfall and natural monument in Cayo, Belize.[1] It is surrounded by the Mountain Pine Ridge Forest Reserve. The Thousand Foot Falls is thought to be the highest waterfall in the Central American region. Despite what its name suggests, this massive waterfall is actually 1,600 ft tall. References ^ Belize Tropical Forest Studies (2010). Thousand Foot Falls Natural Monument. Biodiversity and Environmental Resource Dat...

The Leidsepoort is a former city gate in Amsterdam, the Netherlands, located on what today is Leidseplein square. It was built in 1664 after a design by the city architect Daniël Stalpaert in 1664.[1] It was torn down for traffic purposes in 1862.[2] References ^ History of the Leidseplein[permanent dead link] on Amsterdam City Archives ^ Information about the Leidsepoort on tourist website (on the history of the Leidseplein) External links Media related to Leidsepoor...

Kanbayashi Snowboard Park is a park located in Yamanouchi, Nagano, Japan. Constructed in 1995, it hosted the snowboarding half-pipe events for the 1998 Winter Olympics. References 1998 Winter Olympics official report. Volume 2. pp. 209–11. Shinmai.co.jp venue profile for the 1998 Winter Olympics. Snowjapan.com profile Worldsnowboardguide.com profile vte Venues of the 1998 Winter Olympics (Nagano) Aqua Wing Big Hat Hakuba Ski Jumping Stadium Happōone Resort Iizuna Kogen Ski Area Kanbay...

Lithuanian basketball player Giedrius GustasGustas playing with the Lithuanian national team.Personal informationBorn (1980-03-04) 4 March 1980 (age 43)Kaunas, Lithuanian SSR, Soviet UnionNationalityLithuanianListed height1.90 m (6 ft 3 in)Listed weight84 kg (185 lb)Career informationPlaying career1998–2016PositionPoint guard / shooting guardCareer historyAs player:1998–2004Žalgiris Kaunas2004–2005Lokomotiv Rostov2005–2006Barons LMT2006–2007Dynamo Mosc...

World of WarcraftCover of the first issuePublication informationPublisherWildStormScheduleMonthlyGenre Fantasy, war Publication dateNovember 2007 – December 2009No. of issues30 (25 monthly issues, 4-issue mini-series and 1 special)Creative teamCreated byBlizzard EntertainmentWritten byWalt SimonsonLouise SimonsonArtist(s)Mike BowdenPop MhanPenciller(s)Ludo LullabiJon BuranJon BuranInker(s)Sandra HopeJerome K. MoorePhillip MoyTrevor ScottAndy SmithWalden WongLetterer(s)Nick Na...